Số nguyên tố
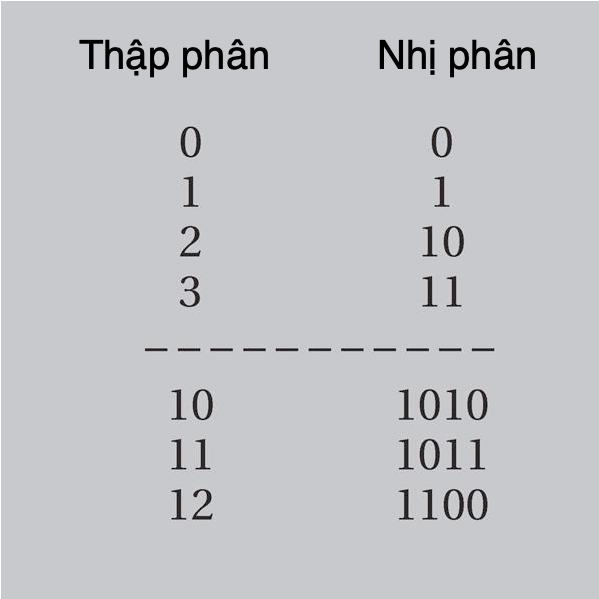
Số nguyên tố là các số nguyên dương chỉ chia hết cho 1 và chính nó. Mười một số đầu tiên là 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, và 31. Có vô hạn số nguyên tố. Theo quy ước, 1 không được xem là số nguyên tố, còn 2 là số nguyên tố chẵn duy nhất. Một con số không phải 1 không phải số nguyên tố thì được gọi là hợp số.
Mỗi hợp số có thể được viết duy nhất dưới dạng một tích của các thừa số nguyên tố nhân nhau: ví dụ, 12 = 22 ´ 3, 21 = 3 ´ 7, và 270 = 2 ´ 33 ´ 5. Vì các số nguyên tố không thể là thừa số của chúng, nên chúng có thể được xem là những viên gạch cấu trúc cơ bản của số nguyên dương. Tuy nhiên, việc xác định một con số có là số nguyên tố hay không, và tìm các thừa số nguyên tố nếu như nó không phải, có thể là bài toán cực kì khó. Bởi thế, quá trình này là một nền tảng lí tưởng cho các hệ thống mã hóa.
Có nhiều kiểu hình sâu sắc cho các số nguyên tố, và một trong những giả thuyết nổi bật nhất của toán học, giả thuyết Riemann, nói về sự phân bố của chúng.
Ước số và số dư
Một con số là ước số của số khác nếu nó phân chia chính xác con số đó, không có số dư. Vậy nên 4 là ước số của 12, vì nó có thể chia 12 thành ba phần bằng nhau. Ở loại phép toán, con số bị đem chia ra, 12, được gọi là số bị chia.
Thế còn 13 chia cho 4 thì sao? Trong trường hợp này, 4 không phải là ước số của 13, vì nó chia 13 thành ba lần, nhưng còn dư lại 1. Một cách biểu diễn đáp số trên là ba, dư một. Đây là một cách khác nói rằng 12, bằng 3 ´ 4, là số nguyên lớn nhất nhỏ hơn số bị chia (13) vốn chia hết cho bốn, và rằng 13 = 12 + 1. Khi số dư một bây giờ đem chia cho bốn, kết quả là phân số , cho nên đáp số cho câu hỏi ban đầu của chúng ta là .
3 và 4 đều là ước số của 12 (cùng với 1, 2, 6 và 12). Nếu chúng ta chia một con số tự nhiên, ví dụ p, cho một số tự nhiên khác, q, không phải là ước số của p, thì luôn luôn có số dư, r, nhỏ hơn q. Điều này có nghĩa là nói chung p = kq + r, trong đó k là một số tự nhiên, và r là một số tự nhiên nhỏ hơn q.
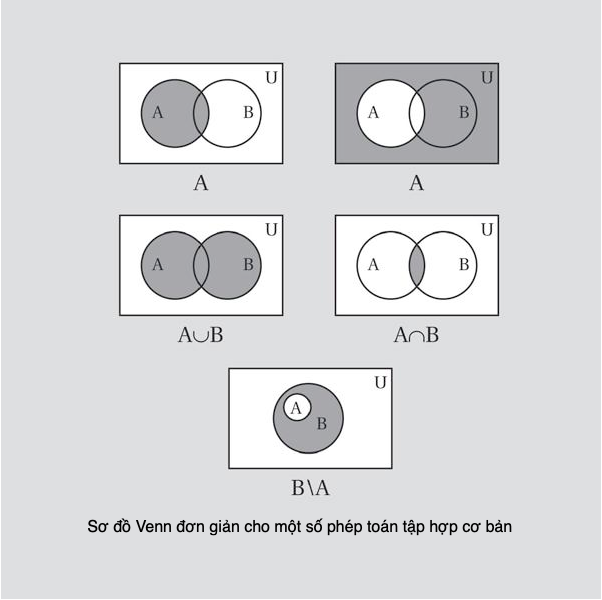
Với hai số p và q bất kì, ước số chung lớn nhất, UCLN, còn gọi là thừa số chung lớn nhất, là con số lớn nhất là ước số của cả p và q. Vì 1 hiển nhiên là ước số của cả hai số, nên UCLN luôn luôn lớn hơn hoặc bằng 1. Nếu UCLN bằng 1, thì hai con số đó được gọi là nguyên tố cùng nhau – chúng không có chung ước số nào ngoại trừ 1.
Các ước số làm nảy sinh một kiểu số thú vị gọi là “số hoàn hảo”. Đây là các con số có tổng các ước số dương, không kể chính chúng, bằng với giá trị của chính nó. Số hoàn hảo đầu tiên và đơn giản nhất là 6 bằng tổng của các ước số của nó, 1, 2, và 3. Số hoàn hảo thứ hai là 28, bằng 1 + 2 + 4 + 7 + 14. Bạn phải chờ rất lâu mới tới lượt số thứ ba: 496, bằng 1 + 2 + 4 + 8 + 16 + 31 + 62 + 124 + 248.
Số hoàn hảo hiếm gặp, và việc tìm chúng là một thách thức. Các nhà toán học vẫn chưa tìm thấy đáp số cuối cùng cho một số câu hỏi quan trọng, ví dụ như có vô hạn số hoàn hảo hay không, hoặc chúng có phải đều là số chẵn hay không.
TOÁN HỌC CẤP TỐC
Paul Glendinning | Bản dịch của Thuvienvatly.com
Phần tiếp theo >>
