Số không
Số không (zero) là một ý tưởng phức tạp, và trong một thời gian dài đã có sự miễn cưỡng triết lí trong việc công nhận và đặt tên cho nó. Hệ thống số Babylon thuở xưa, chẳng hạn, sử dụng một kí hiệu giữ chỗ cho zero khi nó rơi vào giữa các số khác, nhưng không có zero ở tận cùng một con số. Zero được sử dụng dứt khoát và sớm nhất với vai trò một con số như bao số khác là bởi các nhà toán học Ấn Độ vào khoảng thế kỉ thứ chín.
Ngoài những e ngại triết lí, các nhà toán học ngày xưa miễn cưỡng chấp nhận zero bởi vì nó không phải lúc nào cũng hành xử giống những con số khác. Chẳng hạn, chia cho zero là một phép toán vô nghĩa, và nhân bất kì số nào với zero đều bằng zero hết. Tuy nhiên, trong phép cộng zero có vai trò giống như vai trò của số một trong phép nhân. Nó được gọi là phần tử trung hòa của phép cộng, do bởi bất kì con số nào cộng với zero đều cho kết quả bằng chính nó.

Vô cực
Vô cực (biểu diễn toán học là ∞) đơn giản là khái niệm về sự vô tận: một đối tượng vô cực là một đối tượng không bờ bến. Thật khó để làm toán mà không bắt gặp vô cực ở dạng này hay dạng khác. Nhiều lập luận và kĩ thuật toán hoặc liên quan đến việc chọn ra thứ gì đó từ một danh sách vô hạn, hoặc là nhìn vào những gì xung quanh nếu một quá trình nào đó được phép kéo dài đến vô hạn, tiếp tục tiến tới giới hạn vô tận của nó.
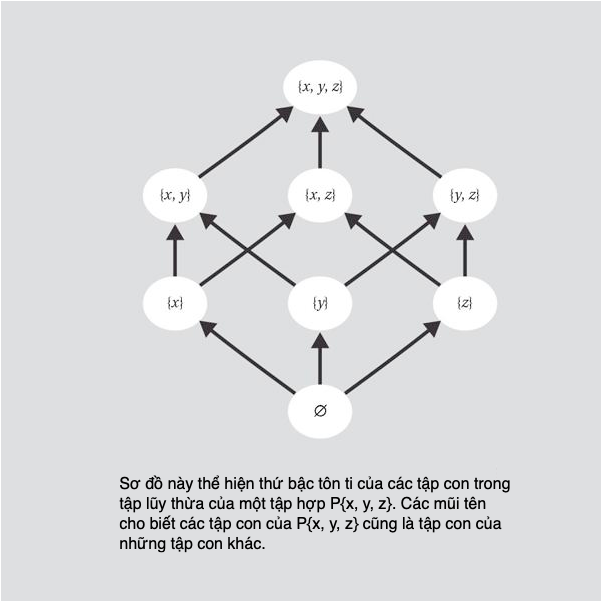
Các tập hợp vô hạn con số hay vô hạn đối tượng khác, được gọi là tập hợp vô hạn, là một bộ phận chủ chốt của toán học. Mô tả toán học của những tập hợp như thế dẫn tới kết luận thật đẹp rằng có nhiều hơn một kiểu tập hợp vô hạn, và vì thế có một số kiểu vô cực khác nhau.
Thật vậy, có nhiều vô số kiểu tập hợp vô hạn, càng lúc càng to, và trong khi điều này có vẻ phản trực giác, song nó tuân theo lô gic của các định nghĩa toán học.

TOÁN HỌC CẤP TỐC
Paul Glendinning | Bản dịch của Thuvienvatly.com
Phần tiếp theo >>