e
e là một số siêu việt và là một trong những hằng số cơ bản của toán học. Được gọi là hằng số Euler, nó có giá trị xấp xỉ 2,71828182845904523536028747. Vị trí tự nhiên của nó là trong giải tích toán học, và mặc dù các kĩ sư và nhà vật lí vui vẻ làm việc với lũy thừa của mười và lograrithm cơ số mười, nhưng các nhà toán học hầu như luôn làm việc với lũy thừa của e và logarithm cơ số e. Đây là logarithm tự nhiên.
Giống như p, e có nhiều định nghĩa. Nó là số thực duy nhất mà đạo hàm của hàm số ex, hàm số mũ, bằng chính nó. Nó là một tỉ lệ tự nhiên trong xác suất; và nó có nhiều biểu diễn theo các số hạng của các tổng vô hạn.
e liên hệ mật thiết với p, vì các hàm lượng giác, thường dùng p biểu diễn, cũng có thể được định nghĩa bằng hàm số mũ.
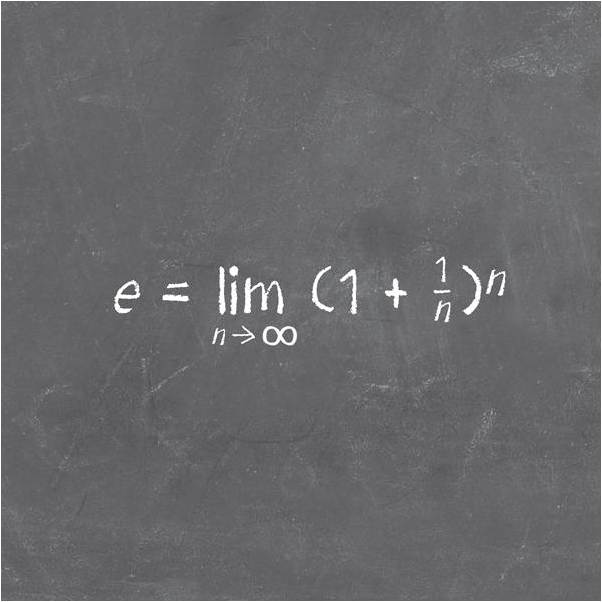
Logarithm
Logarithm là một cách hữu ích để đo bậc độ lớn của một con số. Logarithm của một con số là số mũ mà với nó một con số nhất định, cơ số, phải lũy thừa để đem lại con số đã cho. Giả sử a là số cho trước, b có thể biểu diễn là 10a thì ta nói a là logarithm cơ số 10 của b, kí hiệu là log(b). Vì ta có thể thu được tích của một con số lũy thừa các số mũ khác nhau bằng cách cộng các số mũ đó, nên ta cũng có thể sử dụng logarithm để thu được mọi phép nhân có chứa số mũ.
Như vậy, bằng cách đặt an = x và am = y, thì quy tắc an.am = an + m có thể viết ở dạng logarithm là log(xy) = log(x) + log(y), còn là log(xw) = wlog(x).
Các quy tắc này được dùng để đơn giản hóa các phép tính lớn trong thời đại chưa có máy tính điện tử, bằng cách sử dụng các bảng logarithm hay các thước trượt – hai cái thước với thang chia logarithm chuyển động trên nhau, trong đó việc cộng các thang chia đem lại phép nhân.

TOÁN HỌC CẤP TỐC
Paul Glendinning | Bản dịch của Thuvienvatly.com