Toán học cấp tốc (Phần 18)

Lí thuyết xác suất

Xác suất là một nhánh toán học nghiên cứu việc đo và dự báo khả năng của những kết cục nhất định. Nó vừa là ứng dụng của lí thuyết tập hợp, vừa tự nó là một lí thuyết hoàn toàn mới. Một cách nhìn vào các xác suất là coi một phạm vi kết quả khả dĩ là các phần tử của một tập hợp. Ví dụ, gieo ngẫu nhiên một đồng xu ba lần. Tập hợp mọi kết cục khả dĩ có thể biểu diễn bằng các phần tử chứa ba kí tự, mỗi kí tự cho một kết quả gieo, với N cho mặt ngửa và S cho mặt sấp. Rõ ràng tập hợp này có tám phần tử:

{SSS, SSN, SNS, SNN, NSS, NSN, NNS, NNN}

Vì phải xảy ra một trong những kết cục này, nên tổng của tất cả những xác suất này phải bằng 1, và nếu đồng xu được gieo ngẫu nhiên và mỗi kết cục có khả năng như nhau, thì khả năng của mỗi trường hợp là 1/8.

Những câu hỏi phức tạp hơn về xác suất có thể được trả lời bằng cách xét những kết cục nhất định là các tập con của tập hợp gồm mọi kết cục khả dĩ trước đó.

Chẳng hạn, ta có thể thấy ngay rằng tập hợp các kết cục có đúng hai mặt ngửa gồm ba phần tử, vậy nên có xác suất là 3/8.

Thế còn xác suất để có đúng một lần gieo là ngửa, biết rằng ít nhất một lần gieo là sấp? Nếu chúng ta biết ít nhất một lần gieo là sấp thì ta có thể ràng buộc tập hợp kết cục như sau:

{SSS, SSN, SNS, SNN, NSS, NSN, NNS}

Ba phần tử của tập hợp này, trong số bảy cả thảy, có đúng một mặt ngửa – vì thế xác suất là 3/7.

Những lập luận tương tự nhưng tổng quát hơn đã cho phép các nhà toán học phát triển một tập hợp tiên đề cho xác suất, viết theo các thuật ngữ xác suất về tập hợp và các phép toán được định nghĩa trên tập hợp.

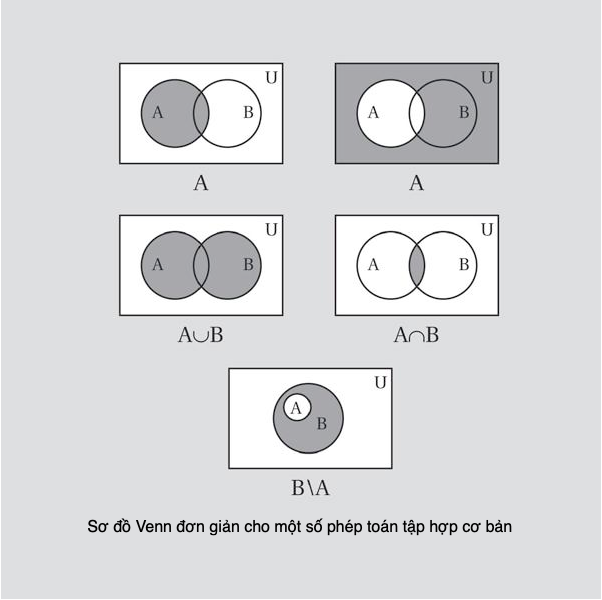
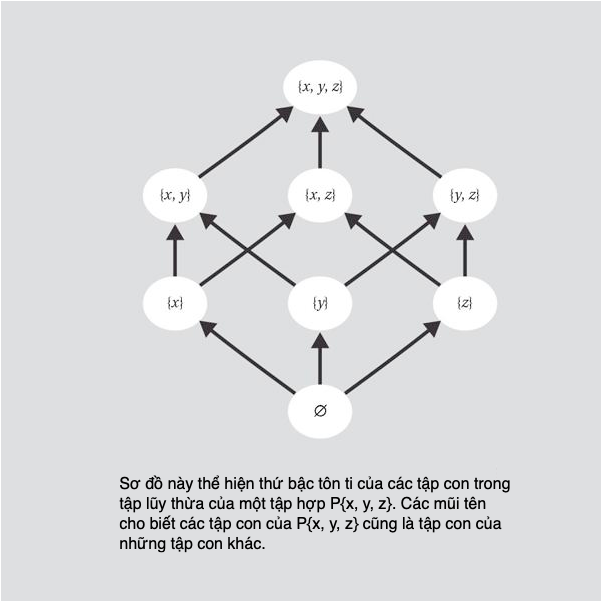
Tập lũy thừa

Tập lũy thừa của một tập S cho trước là tập hợp gồm mọi tập con của S, bao gồm cả S và tập rỗng. Thế nên giả sử S = {0, 1}, thì tập lũy thừa của nó, kí hiệu là P(S) là {F, {0}, {1}, {0, 1}}.

Nhà toán học Đức Georg Cantor đã dùng tập lũy thừa chứng minh rằng có nhiều vô số họ vô cực càng lúc càng lớn, sử dụng một lập luận có phần giống, dù rằng có trước, nghịch lí thợ cạo.

Luận cứ đường chéo của Cantor đã chỉ ra rằng có ít nhất hai kiểu tập hợp vô hạn – tập hợp đếm được, hay lập danh sách được, và tập hợp không đếm được ví dụ như tập liên tục, tập số thực. Bây giờ Cantor chứng minh rằng nếu S là một tập vô hạn thì tập lũy thừa của nó sẽ luôn lớn hơn S, hiểu theo nghĩa là chẳng có cách nào lấy tương ứng các phần tử của S với các phần tử của P(S) sao cho mỗi phần tử trong một tập hợp gắn liền với một và chỉ một phần tử thuộc tập hợp kia. Nói cách khác, lực lượng của P(S) luôn lớn hơn lực lượng của S.

Tập lũy thừa