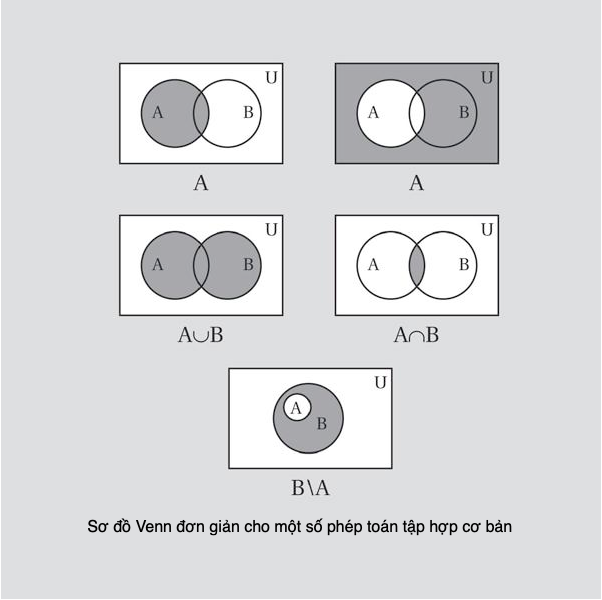
Tập trù mật
Trù mật là một tính chất mô tả mối liên hệ giữa các tập hợp và tập con của chúng khi giữa các phần tử của các tập hợp đó có khái niệm khoảng cách. Nó đem lại một cách đánh giá “cỡ” tương đối của các tập hợp vô hạn khác so với việc đếm các phần tử. Chẳng hạn, một cách xây dựng ý nghĩa rằng số hữu tỉ là một tập hợp “rất lớn” là chúng trù mật trong một tập con đặc biệt, trong trường hợp này là số thực, chính tập này là “rất lớn”.
Một tập X được nói là trù mật trong một tập Y khác, nếu X là một tập con của Y, và một điểm bất kì trong X hoặc là một phần tử của Y, hoặc ở gần tùy ý đến một phần tử: ứng với mỗi điểm trong Y ta có thể chọn khoảng cách d bất kì lớn hơn 0 và tìm thấy một điểm trong X nằm bên trong khoảng cách d đến điểm đó.
Để chứng minh số hữu tỉ trù mật trong số thực, chẳng hạn, chúng ta chọn một khoảng cách d và một số thực y, rồi chứng minh rằng luôn luôn có một số hữu tỉ x nằm trong cự li d đến y, điều đó được thực hiện bằng cách xét bớt phần mở rộng thập phân của y.

Tập hợp không đếm được
Tập hợp không đếm được là tập hợp vô hạn có các phần tử không thể sắp xếp theo một trật tự đếm. Sự tồn tại của những tập hợp như thế có nghĩa là có ít nhất hai kiểu tập hợp vô hạn, đếm được và không đếm được, và hóa ra thì có nhiều vô số kiểu tập hợp không đếm được. Làm thế nào ta có thể chứng minh một tập hợp là đếm được? Vào năm 1891, nhà toán học Đức Georg Cantor đã dùng chứng minh phản chứng để chỉ ra rằng tập hợp gồm các số thực giữa 0 và 1 là không đếm được. Nếu nó đếm được, theo ông lập luận, thì có một danh sách vô hạn nhưng đếm được của các phần tử của nó, mỗi phần tử có thể được viết ở dạng:
0,a1a2a3a4…
trong đó mỗi chữ số ak là một số tự nhiên giữa 0 và 9.
Cantor phủ nhận mệnh đề này bằng cách chỉ ra rằng người ta luôn có thể xây dựng một số thực giữa 0 và 1 không nằm trong danh sách này. Giả sử số thứ k trong danh sách là số thực có phần triển khai thập phân:
0,ak1ak2ak3ak4…
Trong trường hợp đó, ta có thể viết một con số không nằm trong danh sách bằng cách nhìn vào số thứ nhất trong danh sách, k = 1, và chọn chữ số đầu tiên trong phần triển khai thập phân của con số mới của chúng ta bằng 7 nếu a11 = 6, và bằng 6 nếu ngược lại. Để chọn chữ số thứ hai, ta áp dụng quy tắc giống vậy, nhưng sử dụng chữ số thứ hai của số thứ hai trong danh sách. Chữ số thứ ba được tìm từ số thứ ba, và cứ thế:
0,a11a12a13a14…
0,a21a22a23a24…
0,a31a32a33a34…
Cuối quá trình vô hạn này, ta sẽ có một con số có phần triển khai thập phân chỉ gồm các chữ số 6 và 7 và khác với bất kì con số thứ n nào ở chữ số thập phân thứ n – vì thế danh sách ban đầu là không hoàn chỉnh, và tập hợp là không đếm được. Đây gọi là luận cứ chéo của Cantor.
TOÁN HỌC CẤP TỐC
Paul Glendinning | Bản dịch của Thuvienvatly.com