Kết hợp các tập hợp
Cho hai tập hợp bất kì, ta có thể sử dụng các phép toán khác nhau để tạo ra những tập hợp mới, một vài phép toán đó có kí hiệu riêng của nó.
Giao của hai tập hợp X và Y, viết là X ∩ Y, là tập hợp gồm những phần tử chung vừa của X vừa của Y, còn hợp của X và Y, viết là X U Y, là tập hợp gồm mọi phần tử có mặt trong ít nhất một tập hợp X hoặc Y.
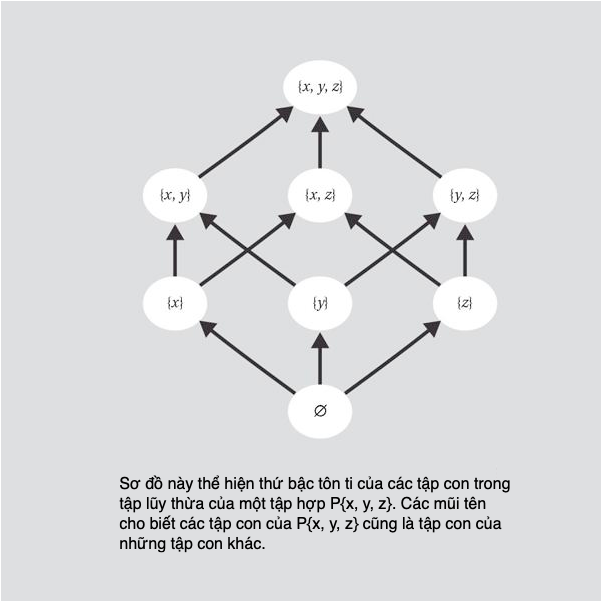
Tập rỗng, kí hiệu là { } hoặc ø, là tập hợp không chứa phần tử nào. Tập con của một tập X là một tập hợp có các phần tử nều nằm trong X. Nó có thể bao gồm một số hoặc mọi phần tử của X, và tập rỗng là tập con của bất kì tập hợp nào.
Tập bù của Y, còn gọi là not Y và viết là Ÿ, là tập hợp gồm các phần tử không có mặt trong Y. Nếu Y là một tập con của X, thì tập bù tương đối của Y, viết là X \ Y, là tập hợp gồm các phân tử có trong X và không có trong Y, và tập này thường được gọi là X not Y.
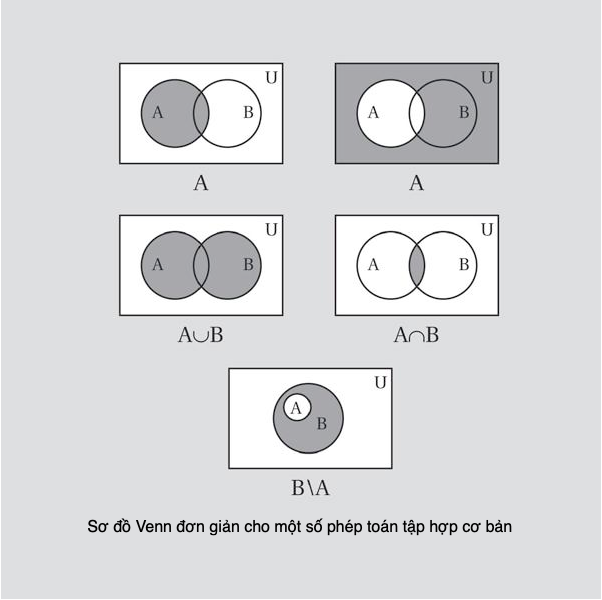
Sơ đồ Venn
Sơ đồ Venn là những hình vẽ trực quan đơn giản được sử dụng rộng rãi để mô tả mối liên hệ giữa các tập hợp. Ở hình thức đơn giản nhất của chúng, người ta dùng một hình đĩa để biểu diễn mỗi tập hợp, và phần giao của các đĩa kí hiệu cho giao của các tập hợp.
Việc sử dụng các sơ đồ như thế để thể hiện mối liên hệ giữa các mệnh đề triết lí hay các tập hợp khác nhau đã có từ nhiều thế kỉ trước. Nó được chính thức hóa bởi nhà lô gic học và nhà triết học người Anh John Venn vào năm 1880. Bản thân Venn gọi chúng là các vòng tròn Euclid khi ông tham khảo các kiểu hình vẽ giống vậy được phát triển bởi nhà toán học Thụy Sĩ Leonhard Euler vào thế kỉ mười tám.
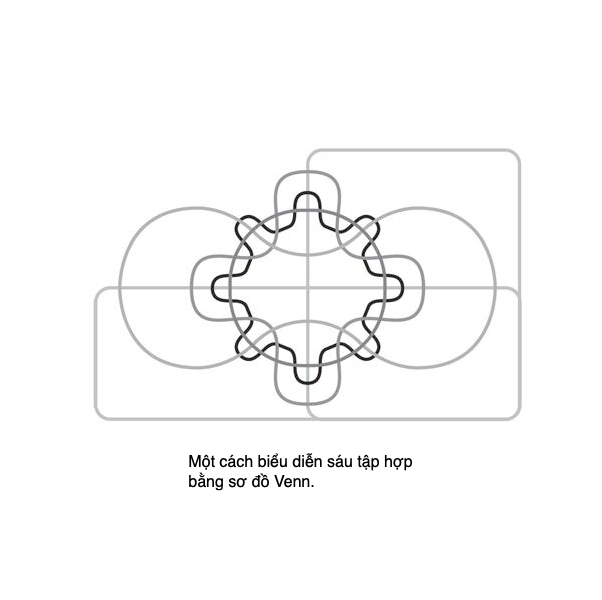
Với ba tập hợp, có một cách cổ điển biểu diễn hết các mối liên hệ khả dĩ (xem trang tập hợp). Còn đối với nhiều hơn ba tập hợp, sắp xếp của các phần giao nhanh chóng trở nên phức tạp hơn nhiều. Sơ đồ ở trang sau thể hiện một cách liên hệ sáu tập hợp khác nhau.
TOÁN HỌC CẤP TỐC
Paul Glendinning | Bản dịch của Thuvienvatly.com