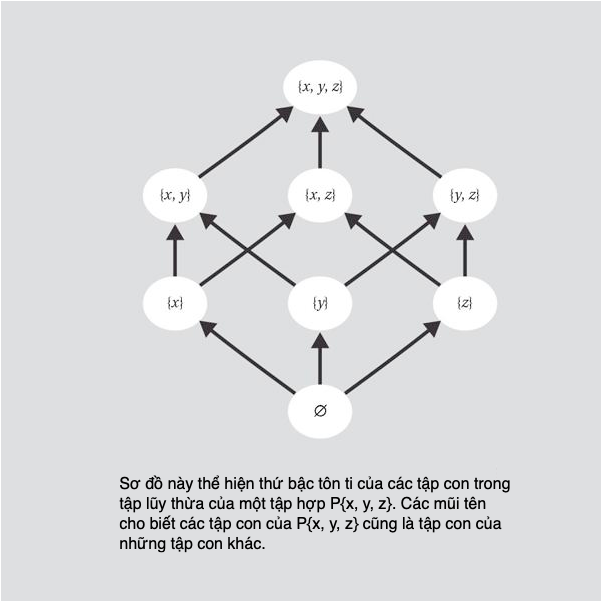
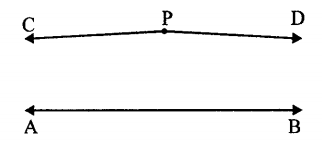
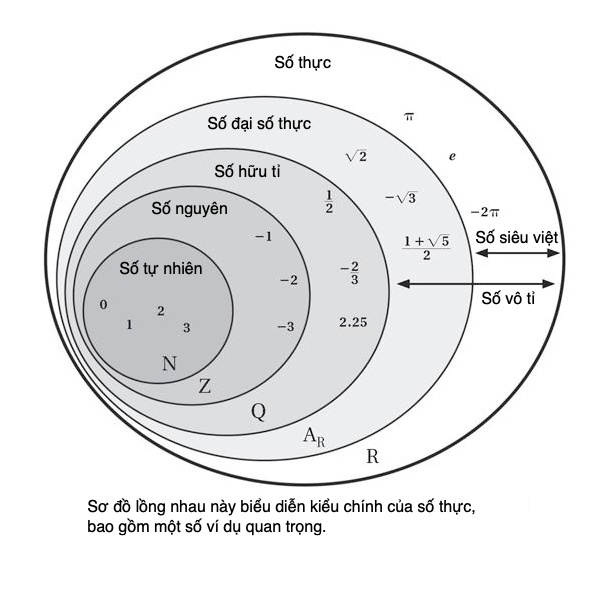
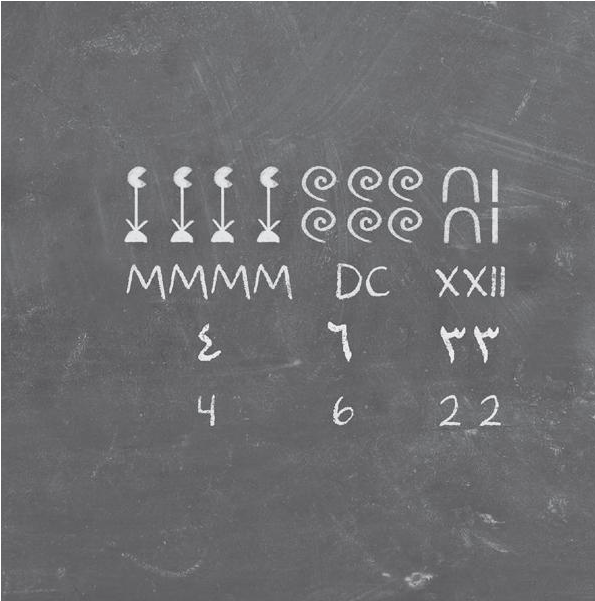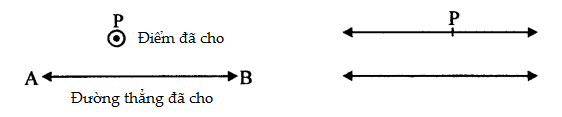Số đại số và số siêu việt
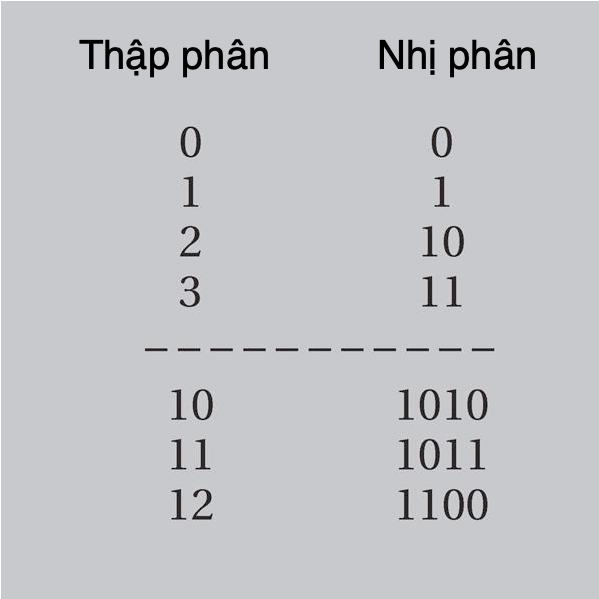
Một số đại số là nghiệm của một phương trình chứa lũy thừa của biến x, một đa thức với các hệ số hữu tỉ, còn số siêu việt không là nghiệm như thế. Hệ số trong các phương trình như vậy là từng số nhân của biến. Ví dụ, Ö2 là số vô tỉ, vì nó không thể được viết dưới dạng tỉ số của hai số nguyên. Nhưng nó là số đại số, vì nó là nghiệm của phương trình x2 – 2 = 0, với các hệ số hữu tỉ (1 và 2). Toàn bộ số hữu tỉ là số đại số, vì mọi tỉ số p/q cho trước đều có thể được tìm thấy là nghiệm của qx – p = 0.
Chúng ta có thể kì vọng số siêu việt là hiếm, song sự thật là ngược lại. Ö2 là ngoại lệ, và hầu như mọi số vô tỉ đều là siêu việt. Chứng minh điều này rất khó, nhưng một con số được chọn ngẫu nhiên giữa zero và một hầu như chắc chắn sẽ là siêu việt. Điều này làm nảy sinh câu hỏi vì sao các nhà toán học dành nhiều thời gian như thế để giải các phương trình đại số, trong khi lại bỏ qua phần lớn các con số.
p
p là một số siêu việt và là một trong các hằng số cơ bản của toán học. Được biểu diễn bởi kí tự Hi Lạp p, nó có mặt ở nhiều nơi đa dạng và bất ngờ. Nó quan trọng đến mức một số nhà toán học và nhà khoa học máy tính đã dành rất nhiều thời gian và nỗ lực nhằm tính nó ngày một chính xác hơn. Vào năm 2010, người ta báo cáo số lượng chữ số thập phân lớn nhất tính được, tất nhiên, bằng một máy tính, là hơn 5 nghìn tỉ!
Với mọi mục đích thực tiễn, không cần độ chính xác lắm, p có thể được lấy xấp xỉ bằng các số hữu tỉ 22/7 và 355/113, hoặc theo kí hiệu thập phân, bằng 3,14159265358979323846264338. p được tìm thấy đầu tiên thông qua hình học, có lẽ xa xưa tận năm 1900 tCN ở Ai Cập và Mesopotamia, và nó thường được giới thiệu là tỉ số của chu vi một đường tròn và đường kính của nó. Archimedes đã sử dụng hình học tìm ra biên trên và biên dưới cho giá trị này, và kể từ đó nó đã xuất hiện trong các lĩnh vực rõ ràng chẳng liên quan gì như xác suất và thuyết tương đối.

TOÁN HỌC CẤP TỐC
Paul Glendinning | Bản dịch của Thuvienvatly.com