Sau quyển "Những câu hỏi và bài tập vật lí phổ thông" (L. Tarasov & A. Tarasova), tiếp tục với phong cách trình bày kiểu Hỏi-Đáp, Thuvienvatly.com giới thiệu với các bạn bản dịch của quyển sách “Toán học – Những điều kì thú và những mốc son lịch sử” (A.L. Audichya); bản dịch dựa trên bản in phát hành năm 2008 ở Ấn Độ.
LỜI NÓI ĐẦU
1. Mục đích của quyển sách này là gì?
Để truyền tải đến độc giả mức độ nhận thức toán học cao nhất và giới thiệu những thành tựu toán học xuất sắc.
2. Những thành tựu toán học vừa nói là những thành tựu nào?
Trước hết là sự đa dạng hóa của toán học, tức là trước đây chúng ta có hình học, nay chúng ta có các loại hình học, và các loại đại số thay cho đại số. và các hệ thống số thay cho hệ thống số.
Một số thành tựu khác bao gồm:
Lí thuyết phương trình đại số của Galois;
Định lí không hoàn hảo của Godel;
Chuỗi Fourier và những tập hợp vô hạn;
Lí thuyết nhóm; ma trận; giải tích số phức;
Topo học; giải tích hàm;
Vân vân.
3. Quyển sách này nhắm tới đối tượng độc giả nào?
Nó dành cho những người không chuyên hiếu kì muốn tìm kiếm những câu hỏi nhanh đáp gọn và không muốn sa vào nghiên cứu chi tiết các khái niệm và quan điểm toán học.
4. Nó có yêu cầu gì đối với độc giả trẻ tuổi hay không?
Có. Ở đây, độc giả trẻ cần có một chút cái nhìn toán học vượt ngoài cái họ đã học ở trường.
5. Có phải quyển sách này dự định thay thế cho sách giáo khoa không?
Không hề. Mục tiêu là rất khiêm tốn. Đó là thôi thúc độc giả tiếp tục tìm hiểu những vấn đề được trình bày ở đây.
6. Quyển sách này có sức hút đối với nhà toán học hay không?
Một nhà toán học thường bị trói buộc với một lĩnh vực riêng và hạn chế. Quyển sách này sẽ cung cấp cho anh ta một cái nhìn tổng quát của toán học.
Quyển sách này cũng sẽ hỗ trợ anh ta tìm kiếm câu trả lời cho những mơ hồ triết lí trong toán học. Nhân thể, mỗi môn học luôn có những mơ hồ như thế.
7. Quyển sách chia làm ba phần chính. Có cần đọc chúng theo thứ tự hay không?
Không cần thiết. Muốn đọc phần nào trước cũng được.
Cũng không cần thiết đọc tuần tự từng câu hỏi trừ khi chúng thu hút người đọc. Nếu có cái gì đó kém hấp dẫn hoặc không thu hút thì bạn có thể bỏ qua.
Bạn có thể lật lại đọc câu hỏi cũ nếu bạn thấy nó còn hấp dẫn.
8. Tại sao tác giả lại chọn kiểu trình bày hỏi-đáp?
Bởi vì trình bày dài dòng sẽ khiến độc giả phổ thông mau chán, còn dạng hỏi-đáp sẽ giữ được sự chú ý của anh ta.
9. Các câu hỏi tuần tự nhau theo khuôn mẫu gì?
Trong chừng mực logic có thể thôi, nghĩa là một câu hỏi hoặc được đề xuất hoặc phát sinh từ câu hỏi trước đó, hoặc có thể chẳng có liên quan gì.
10. Phong cách trình bày theo kiểu gì?
Các câu trả lời đơn giản, minh bạch và dùng ngôn ngữ dễ hiểu, và càng ngắn gọn càng tốt.
11. Nhưng nếu thỉnh thoảng có những câu trả lời chi tiết không thể tránh khỏi thì sao?
Trong những trường hợp như thế, câu trả lời được chia thành những đoạn nhỏ mà độc giả có thể đọc hết hay không tùy theo khẩu vị và cảm xúc.
12. Yêu cầu căn bản khi đọc quyển sách này là gì?
Yêu thích toán học và những cái liên quan đến toán học.
13. Cần có căn bản toán học gì khi đọc quyển sách này?
Không nhiều. Có kiến thức toán học sơ cấp là đủ.
14. Những chủ đề chính trong chương Hình học là gì?
Bao gồm những chủ đề sau:
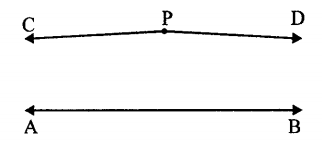
(i) Hình học Euclid và những khái niệm có liên quan.
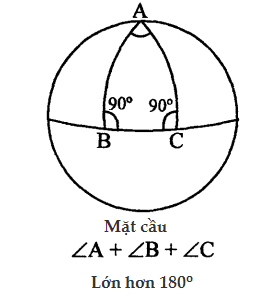
(ii) Hình học Lobachewski và hình học Riemann.
(iii) Hình dạng của Trái đất, không gian và các hạt sơ cấp.
(iv) Hình chiếu.
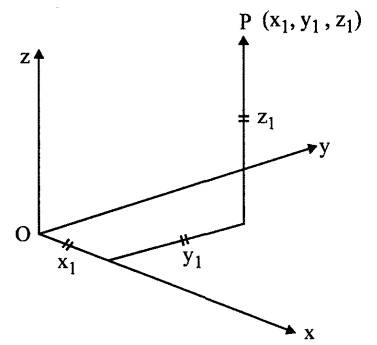
(v) Hình học tọa độ 2, 3, 4 và n chiều.
(vi) Hình học của không gian màu.
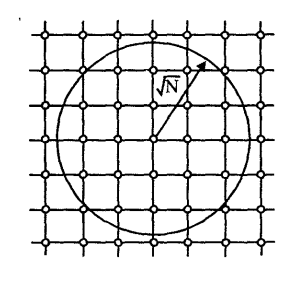
(vii) Hình học hữu hạn.
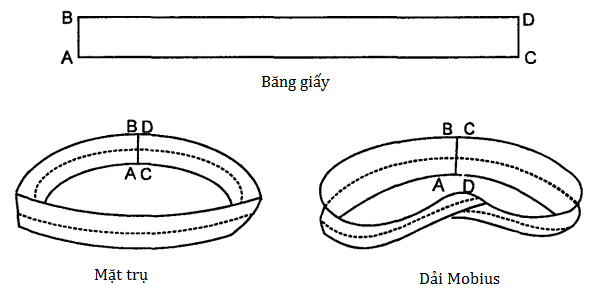
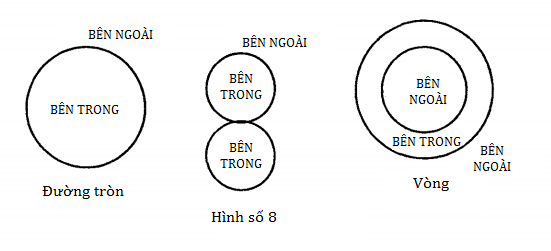
(viii) Topo học.
(ix) Bài toán Cầu nối Koenigsberg.
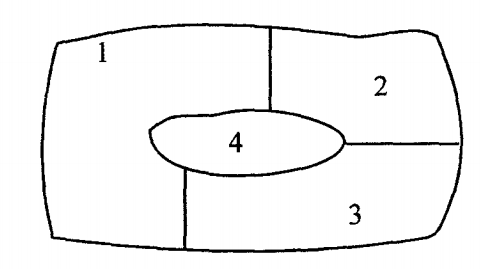
(x) Bài toán bốn màu.
(xi) Phương pháp tiên đề trong hình học.
(xii) Chủ nghĩa hình thức Hilbert.
(xiii) Khám phá của Godel.
15. Những chủ đề chính trong chương Đại số là gì?
Bao gồm những chủ đề sau:
(i) Số học trừu tượng.
(ii) Số học lí thuyết số.
(iii) Mở rộng hệ thống số.
(iv) Lí thuyết phương trình đại số.
(v) Lí thuyết phương trình của Galois.
(vi) Các phương trình Diophantine.
(vii) Đại số trừu tượng.
(viii) Lí thuyết nhóm và những vấn đề có liên quan.
(ix) Vành, vector, ma trận, miền nguyên, trường, không gian vector, đại số tuyến tính.
(x) Không gian Hilbert, không gian Banach.
(xi) Đại số Boole.
(xii) Câu nói năm 1901 của Russel.
(xiii) Tập hợp đếm được và tập hợp không đếm được.
(xiv) Giả thiết liên tục.
(xv) Nghịch lí Barber.
(xvi) Nghịch lí Russel.
16. Những chủ đề chính trong chương Giải tích là gì?
Bao gồm những chủ đề sau:
(i) Giải tích và những khái niệm cơ bản của nó.
(ii) Giới hạn của thương, giới hạn của tổng, và giới hạn của chuỗi vô hạn.
(iii) Nghịch lí Zeno về Achilles và con rùa.
(iv) Chuỗi Fibonacci.
(v) Vi phân và đạo hàm.
(vi) Các ứng dụng hằng ngày của cực đại và cực tiểu.
(vii) Bài toán tia sáng của Heron.
(viii) Tổ ong và sai sót của Koenig.
(ix) Đường cong lấp đầy-không gian.
(x) Đạo hàm riêng và điểm yên ngựa.
(xi) Tích phân và các ứng dụng của nó.
(xii) Tích phân Riemann.
(xiii) Tích phân Lebesgue.
(xiv) Chuỗi Fourier.
(xv) Hệ phương trình vi phân.
(xvi) Hệ phương trình Laplace.
(xvii) Hệ phương trình Maxwell.
(xviii) Hệ phương trình tích phân.
(xix) Các hàm biến phức.
(xx) Các hàm giải tích và dòng chất lưu.
(xxi) Khám phá của Zukovskii.
(xxii) Hàm zeta của Riemann.
(xxiii) Giải tích nhiều biến.
(xxiv) Lí thuyết phân bố.
(xxv) Giải tích thực.
(xxvi) Giải tích hàm.
(xxvii) Gần đúng của các hàm.
(xxviii) Toán rời rạc.
(xxix) Toán học lí thuyết và toán học ứng dụng.
(xxx) Giải tích hiện đại.
17. Nên đọc quyển sách như thế nào?
Trước tiên hãy đọc câu hỏi. Nếu bạn nghĩ bạn không biết câu trả lời thì cứ đọc tiếp. Nhưng nếu bạn nghĩ mình có câu trả lời hợp lí thì hãy tạm dừng một chút và đoán xem câu trả lời là gì. Tiếp theo hãy đọc câu trả lời và kiểm tra xem dự đoán của bạn có đúng không. Nếu bạn đúng thì bạn sẽ có một niềm vui nho nhỏ và niềm tin nữa, còn nếu không thì bạn có câu trả lời trong tay rồi.
18. Nội dung quyển sách có xuất xứ từ đâu?
Trong một quyển sách như thế này, thật không thể nào nhớ nổi một quan điểm hay một khái niệm lần đầu tiên tác giả bắt gặp là nằm ở đâu. Tác giả vay mượn các ý tưởng từ nhiều người và nhiều tác giả khác.
19. Tác giả có muốn cảm ơn ai không?
Quyển sách này được xuất bản là nhờ sự quan tâm liên tục của con gái tôi, Kiran Bhatt, và sự cố gắng bền bỉ, không mệt mỏi của tiến sĩ Latika Jha. Họ đáng được cảm tạ đặc biệt. Nhưng tôi không muốn cảm ơn họ. Tôi dành cho họ chỗ đề tặng của bản in lần thứ nhất này của quyển sách.
Tôi đặc biệt cảm tạ đội ngũ biên tập và xuất bản của nhà xuất bản Messrs. ABD, đặc biệt là Shri Gopal vì sự sắc sảo và hợp tác trong khâu thiết kế và in ấn quyển sách.
20. Còn những góp ý cải tiến quyển sách thì sao?
Các phê bình và góp ý cải tiến quyển sách luôn được hoan nghênh.
-- A.L. Audichya

Toán học – Những điều kì thú và những mốc son lịch sử
Trần Nghiêm dịch
| Phần tiếp theo >>