Toán học – Những điều kì thú và những mốc son lịch sử (Phần 3)

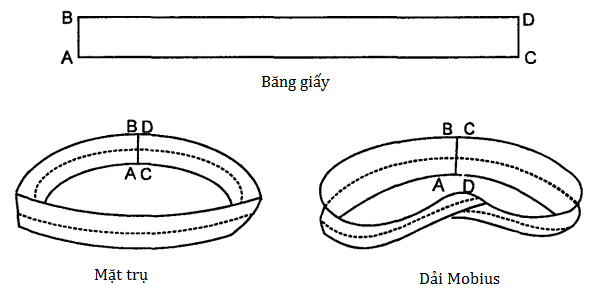
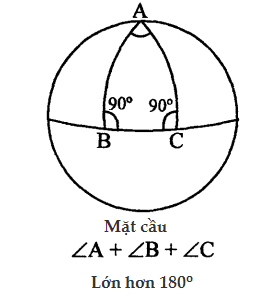
13. Những khái niệm căn bản của hình học Euclid là gì?

Trong hình học Euclid, điểm và đường là những khái niệm căn bản. Một điểm được nói là không có độ lớn, và một đường thì không có bề rộng.

Nhưng đây là những mô tả gợi mở chứ không phải những định nghĩa toán học.

14. Các điểm và đường trong hình học khác như thế nào với các đối tác vật chất của chúng?

Khái niệm điểm là một đối tượng rất nhỏ có hiện thân vật chất là một chấm bút chì. Một đường thẳng tự hiện thân ở một sợi chỉ bị kéo căng hoặc một tia sáng.

Điểm và đường trong hình học là cái trừu tượng từ chấm bút chì và đường kẻ bút chì trong kinh nghiệm hằng ngày.

15. Công dụng của sự trừu tượng ấy là gì?

Ưu điểm từ những trừu tượng như thế là các điểm và các đường trong hình học có những tính chất đơn giản hơn nhiều so với các chấm và các đường vật chất. Ví dụ, hai chấm bút chì đủ to có thể được nối lại bởi nhiều đường kẻ bút chì, nhưng nếu hai cái chấm có kích cỡ càng lúc càng nhỏ, thì toàn bộ các đường kẻ trông hầu như giống hệt nhau và chúng ta chẳng gặp khó khăn gì trong việc nhận thức tiên đề hình học rằng có một và chỉ một đường thẳng có thể được vẽ giữa hai điểm bất kì.

16. Các giả thiết của hình học Euclid là gì?

Các giả thiết của Euclid như sau:

1. Qua hai điểm bất kì, luôn luôn vẽ được một đường thẳng.
2. Đường thẳng có thể kéo dài vô hạn.
3. Với tâm bất kì và bán kính bất kì, luôn luôn vẽ được một đường tròn.
4. Mọi góc vuông đều bằng nhau.
5. Nếu hai đường thẳng tạo thành với một đường thẳng thứ ba hai góc trong cùng phía có tổng nhỏ hơn 180 độ thì chúng sẽ cắt nhau về phía đó.

17. Các tiên đề của hình học Euclid là gì?

Các tiên đề của Euclid như sau:

1. Hai cái cùng bằng cái thứ ba thì bằng nhau.
2. Thêm những cái bằng nhau vào những cái bằng nhau thì được những cái bằng nhau.
3. Bớt đi những cái bằng nhau từ những cái bằng nhau thì được những cái bằng nhau.
4. Trùng nhau thì bằng nhau.
5. Toàn thể lớn hơn một phần.

18. Tiên đề khác với giả thiết như thế nào?

Các tác giả hiện đại thường không nhớ sự phân biệt của Euclid giữa tiên đề và giả thiết, họ sử dụng những tên gọi này nhầm lẫn và gọi chúng là những giả thiết căn bản.

19. Euclid thu được gì từ một tập hợp nhỏ gồm những giả thiết căn bản như thế?

Chỉ sử dụng vài giả thiết căn bản này, Euclid đã chứng minh hàng trăm định lí, nhiều trong số chúng nổi tiếng, và đi đến xếp thứ tự các định lí.

Khái niệm chứng minh, cái cấu thành tinh thần căn bản của toán học, do Euclid nêu ra.

Vì các chứng minh phải được thực hiện hoàn toàn trong khuôn khổ các giả thiết, cho nên sự chọn lựa những giả thiết căn bản của Euclid thật sự là đáng nể và là thành tựu của thiên tài.

20. Định đề hai đường song song là gì?

Giả thiết thứ năm của Euclid đã nói ở trên được gọi là định đề hai đường song song. Một dạng tương đương của định đề trên là như sau:

Qua một điểm cho trước nằm ngoài một đường thẳng cho trước, ta vẽ được một và chỉ một đường thẳng song song với đường thẳng đã cho.

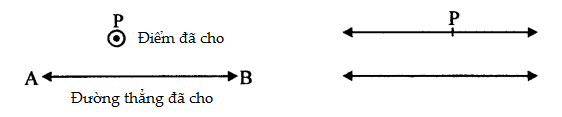
Đây là “định đề hai đường song song” nổi tiếng. Nó thể hiện sự thiên tài của Euclid vì đã nhận ra sự cần thiết của nó.

Một hệ quả logic của định đề này là Định lí Pythagoras phát biểu rằng tổng ba góc của một tam giác luôn bằng 180 độ.

Toán học – Những điều kì thú và những mốc son lịch sử
Trần Nghiêm dịch
Phần tiếp theo >>

Bài trước | Bài kế tiếp