Những vũ trụ khả dĩ
Hầu như mỗi giáo viên dạy toán đều có kinh nghiệm sau đây với các học sinh gặp phải những bài toán bằng lời – học sinh cho biết rằng anh ta chẳng gặp khó khăn gì trong việc giải các phương trình, mà cái khó là lập ra phương trình để giải. Các phương trình trường Einstein là một tình huống hoàn toàn khác; “bài toán bằng lời” của vũ trụ được xác lập trong các phương trình, vấn đề là xác định tháo gỡ những lời đó như thế nào bằng cách giải các phương trình. Một vài người đã giải bài toán này khi thuyết tương đối rộng được công bố, và trong tiến trình đó có một số dây nhợ đã bị bỏ qua.
Người nổ phát súng đầu tiên vào giải các phương trình là bản thân Einstein, đúng như trông đợi bởi vì ông là người đầu tiên biết các phương trình thật sự có mặt mũi ra sao. Thuyết tương đối rộng được công bố vào năm 1916, trước khi Hubble chứng minh có tồn tại những thiên hà nằm ngoài Dải Ngân hà, chứ đừng nói gì đến thực tế các thiên hà đang lùi ra xa nhau. Quan niệm trước đó cho rằng vũ trụ tổng thể là tĩnh tại và bất biến. Vì thế, Einstein muốn tìm ra một nghiệm tĩnh và bất biến. Ông tìm thấy một nghiệm, nhưng nó không phải nghiệm tĩnh và bất biến; vũ trụ mà nó mô tả hoặc bị giãn ra hoặc bị co lại.
Vậy phải làm sao? Einstein tin chắc các phương trình của ông là đúng, vì chúng cho kết quả đúng khi áp dụng cho hệ mặt trời, nhưng có cái gì đó không còn đúng khi xét ở một quy mô lớn hơn. Vì thế, Einstein đã đưa thêm một “hệ số gian lận” vào EFE để thu được một nghiệm sẽ cho một vũ trụ tĩnh và bất biến. Hệ số gian lận này đã biến EFE từ dạng đẹp đơn giản
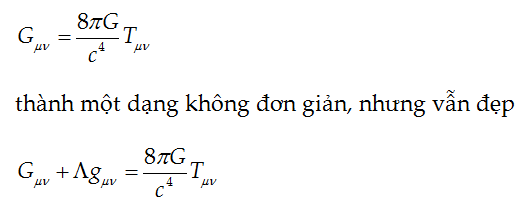
Số hạng bổ sung gồm một hằng số vũ trụ học L nhân với một tensor làm đơn giản hóa phép tính chiều dài và góc hợp bởi các vector tiếp tuyến; nó cho phép người ta tính khoảng cách và hình dung không gian mà tensor mô tả có hình dạng như thế nào. Tác dụng của hằng số vũ trụ học là nó triệt tiêu xu hướng làm nhiễu loạn vũ trụ (theo Einstein) trong nghiệm ban đầu của Einstein hoặc là giãn ra hoặc là co lại. Lí thuyết trong vật lí học (và bất kì ngành nào khác) là thực dụng; bạn cố gắng xây dựng một lí thuyết khớp với thực tế, và vũ trụ mà Einstein biết vào năm 1916 là tĩnh tại và bất biến.
Nghiệm Einstein không phải là nghiệm duy nhất cho các phương trình của ông. Một nghiệm nữa nhanh chóng được tìm ra bởi nhà thiên văn học người Hà Lan Willem de Sitter. Thật không may, giống như nghiệm ban đầu của Einstein, nghiệm de Sitter có vẻ có những đặc điểm phi lí.
Để bắt đầu, vũ trụ của de Sitter, theo giả định, không có chứa khối lượng gì hết cả. Đây chưa phải là khiếm khuyết gì lớn như trông bên ngoài nó như thế, bởi vì, như chúng ta đã thấy trong suốt tập sách này, vũ trụ thực tế mà chúng ta đang sinh sống chỉ chứa một nguyên tử trong mỗi năm mét khối không gian. Láng giềng địa phương của chúng ta có vẻ co cụm nhiều khối lượng, nhưng nếu chúng ta xét một khối cầu, với bán kính lớn hơn một năm ánh sáng một chút, với tâm tại hành tinh quê hương của chúng ta, thì quả cầu đó sẽ có mật độ trung bình chỉ một nguyên tử trong mỗi millimet khối – gần giống như là chân không, và đấy là chúng ta đang nói tới một vùng chứa khá nhiều vật chất. Giả thuyết một vũ trụ trống rỗng của de Sitter khiến những người đối địch của ông xem là phi lí, nhưng rốt cuộc nó là một mô tả thật đẹp của vạn vật. Tuy nhiên, nó không được chào đón nhiệt liệt. Cái khó thứ hai là trong vũ trụ của de Sitter, các đồng hồ ở cách Trái đất những khoảng cách lớn chạy chậm hơn các đồng hồ trên Trái đất. Đây là do hiệu ứng lệch đỏ của ánh sáng đến từ những thiên hà ở xa. Nghiệm de Sitter được mô tả trước khi định luật Hubble được nhiều người biết tới, và cả de Sitter và Eddington đều e rằng ánh sáng lệch đỏ sẽ bị hiểu sai là do vận tốc lùi ra xa. Không có gì bất ngờ, Einstein đã không đào sâu vào những chỗ trũng của nghiệm de Sitter, ông nói rằng với ông nó là vô nghĩa (hãy nhớ rằng lúc ấy Einstein không biết rằng có những thiên hà nằm bên ngoài Dải Ngân hà). De Sitter chỉ ra bằng chứng rằng Slipher đã làm sáng tỏ vấn đề vận tốc lùi ra xa của các ngôi sao, và nhấn mạnh rằng những kết quả này ủng hộ cho mô hình của ông. (Về vấn đề này, tôi xin giơ tay phản đối: làm thế nào vận tốc lùi ra xa của những vật thể vật chất có thể ủng hộ cho nghiệm de Sitter, khi mà chẳng có vật thể vật chất nào trong vũ trụ de Sitter? Tôi không thể tưởng tượng có ai đó lại làm chuyện như thế này tại một hội nghị toán học. Tôi đoán rằng loại câu chuyện như thế này làm cho các hội nghị vũ trụ học mang tính giải trí cao hơn nhiều so với hội nghị toán học.)
Những con số làm nên vũ trụ
James D. Stein
<< Phần trước | Phần tiếp theo >>










![[ebook] Thiên Văn Vật Lí Cho Người Bận Rộn](/bai-viet/images/2019/05/thienvan2.png)