Toán học – Những điều kì thú và những mốc son lịch sử (Phần 18)

11. Đại số trừu tượng là gì? Có phải nó là một sự khái quát hóa hơn nữa?

Trong đại số trừu tượng, ngay cả những thực thể này cũng mất hết ý nghĩa của chúng về phương diện độ lớn và người ta nói tới những “phần tử” khái quát hơn trên đó những toán tử tương tự các toán tử đại số có thể được thực hiện.

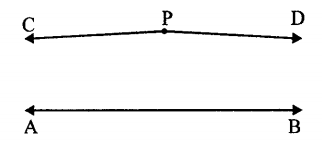
Một ví dụ của những phần tử như thế là hai chuyển động tác dụng liên tiếp nhau hợp lại sẽ tương đương với một chuyển động.

Để minh họa, kí hiệu chuyển động quay của một hình vuông quanh tâm của nó 90^o là R₁, 180^o là R₂ và 270^o là R₃, thì chuyển động quay R₁ rồi đến R₂ sẽ tương đương với một chuyển động R₃.

Một ví dụ nữa là hai phép biến đổi đại số sẽ tạo ra cùng một kết quả với một phép biến đổi đại số.

Để minh họa, kí hiệu phép tịnh tiến là T₁ và T₂ là phép quay, thì biến đổi T₁ rồi đến T₂ sẽ tương đương với một phép tịnh tiến T₃.

Do đó, nếu với một tập hợp nhất định của các “vật”, kí hiệu bằng những chữ cái, những toán tử nhất định có thể được định nghĩa theo những quy tắc nhất định, thì người ta nói một hệ thống đại số đã được định nghĩa. Vì thế, đại số học được nhận dạng là việc nghiên cứu những hệ thống đại số đa dạng, và khi đó nó được gọi là đại số trừu tượng hay đại số tiên đề.

12. Vì sao nó được gọi là đại số trừu tượng hay đại số tiên đề?

Nó là trừu tượng bởi vì chúng ta không quan tâm các chữ cái trong hệ thống đại số đó kí hiệu cho cái gì. Cái quan trọng là các tiên đề hay các quy tắc phải được thỏa mãn bởi các toán tử. Và nó có tính tiên đề bởi vì nó được xây dựng đơn thuần từ các quy tắc hay các tiên đề được phát biểu lúc ban đầu.

Hai hệ thống đại số như thế được gọi là nhóm và vành.

Tên gọi thoạt nghe có chút lạ lẫm, nhưng hiểu qua chút ít sẽ làm dịu đi phản ứng ban đầu đó. Chúng ta sẽ trở lại với chúng ở phần sau.

13. Những lĩnh vực nghiên cứu nào sử dụng đại số tiên đề?

Topo học, giải tích hàm, cơ học lượng tử và vật lí đương đại là một vài cái tên thuộc một vài lĩnh vực quan trọng, trong đó đại số tiên đề tỏ ra là công cụ khảo sát có sức mạnh nhất.

14. Số học là lí thuyết của những con số! Lí thuyết của những con số nghiên cứu cái gì?

Lí thuyết sơ cấp của những con số nghiên cứu cái sau đây:

Các hợp số và các quy tắc chia hết, số nguyên tố và sự xuất hiện của chúng, định lí cơ bản của số học, định lí Fermat, định lí Wilson, định lí cuối cùng của Fermat.

Các số Pythagoras,

Tính chất của những con số lớn,

Những con số được nói tới ở đây là số tự nhiên hoặc số nguyên dương.

15. Hợp số và số nguyên tố là gì?

Một số con số có thể được phân tích thành những thừa số nhỏ hơn, ví dụ 15 = 3 × 5, nhưng 11 hoặc 17 thì không phân tích được.

Các số có thể phân tích được thành những thừa số nhỏ hơn được gọi là hợp số, còn những số không thể phân tích được như thế được gọi là số nguyên tố.

16. Còn số 1 thì sao? Nó có phải là số nguyên tố không?

Một số nguyên tố là số có ước số là 1 và chính nó.

Ví dụ, số nguyên tố 7 có hai ước số, 1 và 7, mặc dù người ta gọi chúng là những ước số tầm thường.

Vì thế, nếu 1 là số nguyên tố thì nó sẽ có đúng hai ước số. Nếu 1 là hợp số, thì nó sẽ có nhiều hơn hai ước số. Nhưng số 1 có đúng một ước số thôi, cho nên nó không phải là số nguyên tố, cũng chẳng phải là hợp số.

17. Các quy tắc chia hết là gì?

Sau đây là các quy tắc chia hết. Người ta học chúng ở nhà trường.

Một số là chia hết cho 2, nếu chữ số hàng đơn vị của nó chia hết cho 2. Như vậy, những số kết thúc với 0, 2, 4, 6, hoặc 8 là chia hết cho 2, như trong 530 và 138.
Một số là chia hết cho 4, nếu hai chữ số tận cùng bên phải là 00 hoặc chia hết cho 4, như trong 300 và 528.
Một số là chia hết cho 8, nếu ba chữ số tận cùng bên phải là 000 hoặc chia hết cho 8, như trong 3000 và 3240.
Một số là chia hết cho 5, nếu chữ số tận cùng bên phải là 0 hoặc 5, như trong 240 và 235.
Một số là chia hết cho 25, nếu hai chữ số tận cùng bên phải là 00 hoặc chia hết cho 25, như trong 300 và 425.
Một số là chia hết cho 3, nếu tổng các chữ số trong số đó chia hết cho 3, như trong 231.

Ở đây 2 + 3 + 1 = 6, tổng chia hết cho 3, vì thế 231 chia hết cho 3.

Ta dễ dàng thấy được nguyên nhân như sau:

231 = 2 × 100 + 3 × 10 + 1

= 2 × (99 + 1) + 3 × (9 + 1) + 1

= 2 × 99 + 2 × 1 + 3 × 9 + 3 × 1 + 1

= 2 × 99 + 2 + 3 × 9 + 3 + 1

= (2 × 99 + 3 × 9) + (2 + 3 + 1)

= (một bội của 9) + (tổng các chữ số).

Do đó, một con số là chia hết cho 3, nếu tổng các chữ số của nó là chia hết cho 3.

7. Một số là chia hết cho 9, nếu tổng các chữ số trong số đó chia hết cho 9, như trong 477.

Ở đây, 4 + 7 + 7 = 18, tổng chia hết cho 9, nên 477 chia hết cho 9.

Lí do trong trường hợp này cũng tương tự như với trường hợp chia hết cho 3.

8. Một số là chia hết cho 11 nếu hiệu giữa tổng của các chữ số thứ tự lẻ và tổng các chữ số thứ tự chẵn bằng 0 hoặc bằng bội của 11.

Xét con số 1 8 3 9 5 5 2.

Tổng các chữ số thứ tự lẻ là 1 + 3 + 5 + 2 = 11,

Tổng các chữ số thứ tự chẵn là 8 + 9 + 5 = 22,

Hiệu bằng 22 – 11 = 11, chia hết cho 11,

nên 1 8 3 9 5 5 2 chia hết cho 11.

18. Còn những quy tắc nào khác nữa không?

Vâng, có những quy tắc hấp dẫn như sau:

Tích của hai số bằng tích của ước chung lớn nhất của chúng và bội chung nhỏ nhất của chúng.
Như vậy, nếu hai số là 12 và 18, thì ước chung lớn nhất và bội chung nhỏ nhất của chúng tương ứng là 6 và 36, và 12 × 18 = 6 × 36 = 216.
Tích của hai số nguyên liên tiếp là chia hết cho 2, tức là n(n + 1) là chia hết cho 2, trong đó n là số nguyên bất kì.
Tích của ba số nguyên liên tiếp, tức là n(n + 1)(n + 2), là chia hết cho 2 × 3, tức là 6.
Tích của bốn số nguyên liên tiếp, tức là n(n + 1)(n + 2)(n + 3) là chia hết cho 2 × 3 × 4, tức là 24.
Tích của r số nguyên liên tiếp là chia hết cho 2 × 3 × 4 × ... × r, hay r! .
Tích 1.2.3...r được gọi là r giai thừa, và được kí hiệu là r!
Với mọi số lẻ n, số n² – 1 là chia hết cho 8.
Nếu n là một số lẻ, thì n – 1 phải chẵn và chia hết cho 2. Đồng thời, n + 1 là số chẵn liền sau và, do đó, chia hết cho 4. Vì thế, tích này chia hết cho 8.