38. Có phải một “đường thẳng” phải kéo dài vô hạn ở cả hai phía không?
Các đường song song trong hình học Euclid không cắt nhau và cho dù kéo dài bao xa về mỗi phía thì chúng vẫn luôn luôn cách nhau một khoảng không đổi. Một đường thẳng, do đó, được cho là kéo dài vô hạn ở cả hai phía.
Riemann đề xuất rằng không có nhu cầu logic nào cho một khái niệm như thế và mọi đường thẳng nếu kéo dài đủ mức có thể quay trở lại trên chúng và có cùng chiều dài giống như các đường kinh tuyến trên bề mặt Trái đất.
Trong trường hợp một hình cầu giống như Trái đất, mỗi kinh tuyến giao cắt với kinh tuyến khác ở hai điểm, đó là cực Bắc và cực Nam, nên mỗi cặp “đường thẳng” luôn luôn cắt nhau và khép kín một diện tích, và không có hai “đường thẳng” nào có thể song song nhau.
39. Nhưng làm thế nào một đường thẳng có thể tuân theo hình học Euclid lẫn hình học Riemann?
Giả thiết ngầm của Euclid ngụ ý rằng một đường thẳng có thể kéo dài ra vô hạn. Theo Riemann, một đường thẳng, nếu kéo dài đủ mức, có thể quay trở lại trên chính nó.
Mâu thuẫn rõ ràng mà Riemann nêu ra là sự khác biệt quan trọng giữa vô hạn và khép kín.
Một đường thẳng có thể khép kín và không vô hạn giống như bề mặt của một quả cầu khép kín nhưng không vô hạn. Một đường thẳng không thỏa mãn yêu cầu nhất quán như thế khớp hoàn toàn với hình học Euclid và hình học Riemann.
40. Cái nào là hình học của Trái đất?
Đối với đa số mục đích thông thường, bề mặt của Trái đất hành xử như thể nó là phẳng. Do đó, để xây dựng nhà cửa, cầu đường, sân chơi thể thao, vân vân, khoảng cách ngắn nhất giữa hai điểm là một đường thẳng và tổng số đo ba góc của một tam giác là 180o, và hình học có thể áp dụng là hình học Euclid.
41. Còn khi xét những khoảng cách lớn trên Trái đất thì sao?
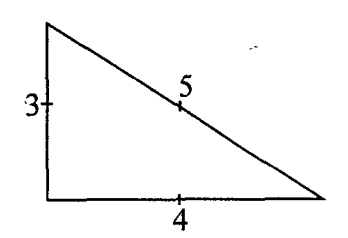
Xét một tam giác lớn trên bề mặt của Trái đất được tạo bởi một cung xích đạo và hai đoạn kinh tuyến, tức là hai đường tròn lớn vẽ từ cực Bắc và kết thúc trên cung này. Xem hình bên dưới:
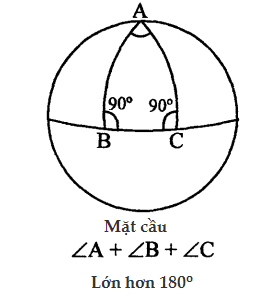
Hai góc đáy mỗi góc bằng 90o nên tổng ba góc của tam giác cộng lại sẽ lớn hơn 180o.
Khoảng cách ngắn nhất giữa hai điểm bất kì không còn là một đường thẳng mà là một đoạn cung kinh tuyến, cho nên hình học Euclid không còn áp dụng được.
Thật vậy, ngay cả khi hai điểm trên bề mặt Trái đất chỉ cách nhau vài trăm mét, thì việc công nhận độ cong của Trái đất sẽ xác định khoảng cách chính xác giữa chúng.
42. Trái đất phẳng bao nhiêu hay cong bao nhiêu?
Một đường thẳng trong một mặt phẳng được nói là thẳng và không có độ cong, còn trong trường hợp đường tròn thì đường tròn càng nhỏ độ cong của nó càng lớn.
Nếu chúng ta lấy một đường tròn bán kính 1 foot là có độ cong đơn vị, thì độ cong của một đường tròn bán kính 1 yard sẽ bằng một phần ba đơn vị; và với tỉ lệ này thì độ cong của đường tròn lớn trên bề mặt Trái đất sẽ vào khoảng một phần 21 triệu. Độ cong này là quá nhỏ nên một cung của một đường tròn như vậy trên thực tế không thể phân biệt với một đoạn thẳng.
Vì thế, hình học của Trái đất là hình học Euclid đối với những chiều dài hay khoảng cách nhỏ, và là hình học phi Euclid đối với những khoảng cách lớn.
43. Hình học của không gian mà chúng ta đang sống là hình học nào?
Gauss, “ông hoàng toán học”, đã chọn ba đỉnh núi ở xa nhau tạo nên một tam giác và tìm thấy tổng số đo ba góc của tam giác được tạo ra đó là bằng 180o trong giới hạn của sai số thực nghiệm.
Thí nghiệm tỏ ra không thuyết phục bởi vì tam giác mà ông sử dụng là đủ lớn so với hình vẽ trên giấy, nhưng vẫn quá nhỏ so với kích cỡ của vũ trụ.
Nếu thay cho ba ngọn núi ở xa, chúng ta chọn ba ngôi sao ở xa, thì thí nghiệm vẫn không thuyết phục, mặc dù lần này là vì những lí do hoàn toàn khác.
44. Những lí do này là gì?
Vì trong trường hợp này, phép đo góc sẽ phải theo phương tiện tia sáng, và trong hành trình xuyên không gian của chúng, những tia sáng này bị bẻ cong theo độ lớn của trường hấp dẫn mà chúng đi qua, cho nên kết quả của phép đo sẽ cho chúng ta biết về các định luật truyền ánh sáng nhiều hơn là về bản chất của không gian, dù là Euclid hay không.
45. Không gian có ý nghĩa chính xác là gì?
Một quan điểm có thể là không gian hoàn toàn trống rỗng, một khoảng không không có vết tích của vật chất, nhưng trong một không gian như vậy không có cái gì để phân biệt một vị trí hay một phương hướng, cho nên không có vị trí, không có phương hướng và, vì thế, không gian hoàn toàn trống rỗng chẳng gì hơn là một sự trừu tượng.
46. Quan điểm khác thì sao?
Quan điểm khác cho rằng “không gian là hình thức tồn tại của vật chất”, cho nên tính chất của không gian thật sự là tính chất của những liên hệ nhất định của các vật thể, ví dụ, kích cỡ của chúng, vị trí tương hỗ, vân vân.
Theo quan điểm này, không gian thật sự không thể chia tách với vật chất. Vật chất xác định hình học và hình học giải thích cho hiện tượng trước đây quy cho lực hấp dẫn.
Không những vậy, như Einstein chứng minh, không gian không thể tách rời với thời gian, và chúng cùng nhau tạo nên một hình thức tồn tại của vật chất, đó là không-thời gian.
47. Nếu không gian và thời gian được xem như những thực thể riêng biệt thì sao?
Cấu trúc của không-thời gian là phức tạp và không gian không thể tách rời với thời gian ngoại trừ dưới những giả thiết nhất định, trong trường hợp đó không gian hóa ra là Euclid trong những vùng nhỏ so với kích cỡ vũ trụ, nhưng trong những vùng lớn có chứa khối lượng lớn vật chất, thì sự sai lệch khỏi hình học Euclid trở nên rõ nét.
48. Hình học gần đúng của vũ trụ là hình học nào?
Nhiều giả thuyết đã được đặt ra về cấu trúc của vũ trụ xem như một tổng thể, giả sử sự phân bố khối lượng là đồng đều và vũ trụ không tĩnh tại.
Những giả thuyết này đã làm đơn giản hóa vấn đề và cho phép chúng ta có một khái niệm gần đúng của khuôn khổ thật sự của vạn vật.
Dưới những giả thuyết như vậy, một lí thuyết đã được đề xuất bởi nhà vật lí Liên Xô Friedmann cho thấy hình học của vũ trụ trên tổng thể là hình học Lobachewsky.
49. Hình học nào áp dụng cho các hạt sơ cấp?
Giống như trường hợp hình học Euclid không áp dụng được cho những khoảng cách lớn trong vũ trụ, nó cũng không áp dụng được cho những khoảng cách cực nhỏ.
Hình học phi Euclid có thể áp dụng cho những khoảng cách bên trong và giữa các nguyên tử, phân tử, hạt sơ cấp, vân vân.
50. Chỉ có ba môn hình học thôi sao?
Rõ ràng là có thể có vô số môn hình học, bởi vì bắt đầu với những tiên đề bất kì người ta có thể xây dựng nên một môn hình học mới, miễn sao các tiên đề đó không dẫn tới mâu thuẫn.
Một bề mặt mới có thể được tìm thấy là nơi áp dụng cho lí thuyết hình học mới.
Tuy nhiên, một bề mặt càng phức tạp, thì bộ môn hình học xây dựng thích hợp cho nó cũng thật kì cục.
Toán học – Những điều kì thú và những mốc son lịch sử
Trần Nghiêm dịch
Phần tiếp theo >>







![[Ảnh] Hình học trong thế giới quanh ta](/bai-viet/images/2012/09/hh01.jpg)