Các kiểu số
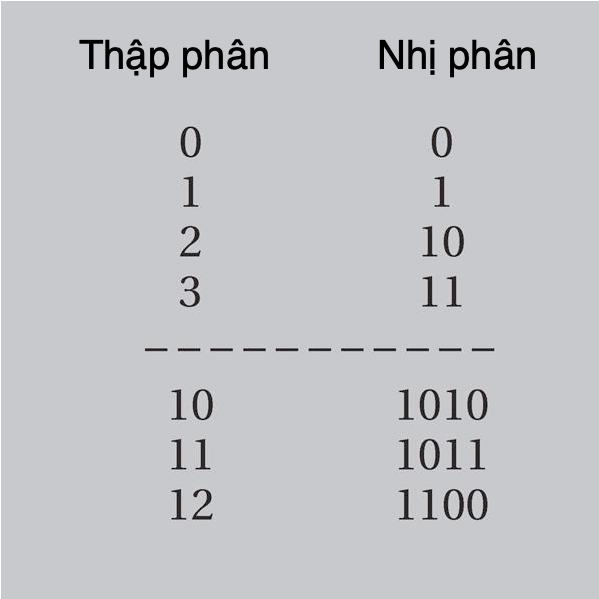
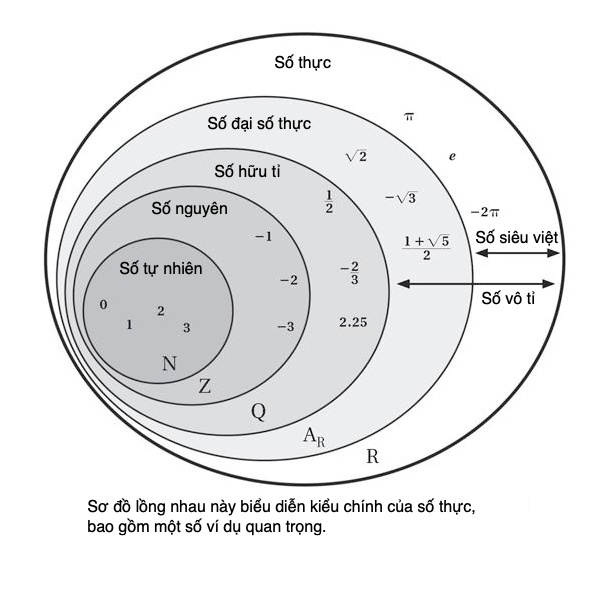
Các con số có thể được chia loại thành các kiểu số có chung những tính chất nhất định. Có nhiều cách đưa các con số vào nhóm theo cách này. Quả vậy, y như việc có vô hạn con số, có vô số cách để chúng được chia nhỏ và phân biệt với nhau. Ví dụ, các số tự nhiên, số nguyên mà chúng ta dùng để đếm các vật trong thời gian thực, đúng là một kiểu như thế, là kiểu số nguyên – số nguyên còn bao gồm những số nhỏ hơn zero. Số hữu tỉ tạo thành một kiểu khác, và giúp định nghĩa một kiểu số lớn hơn nữa, đó là số vô tỉ. Các kiểu số đại số và siêu việt được định nghĩa bởi những hành trạng khác, trong khi các thành viên của mọi kiểu số này đều là thành viên của kiểu số thực, định được định nghĩa đối lập với số ảo.
Nói một con số là thành viên của một kiểu nhất định là một cách vắn tắt mô tả các tính chất của nó, và do đó làm rõ kiểu câu hỏi toán học nào chúng ta có thể nêu ra một cách có ích về nó. Thông thường, các kiểu số nảy sinh từ sự sinh hàm mô tả cách xây dựng một dãy số. Hoặc là, chúng ta có thể xây dựng một hàm số hay một quy tắc mô tả các kiểu mà chúng ta ghi nhận theo bản năng.
Chẳng hạn, theo bản năng chúng ta nhận ra số chẵn, thế nhưng số chẵn là gì? Về mặt toán học, chúng ta có thể định nghĩa chúng là mọi số tự nhiên ở dạng 2 x n, trong đó bản thân n là một số tự nhiên. Tương tự, số lẻ là các số tự nhiên ở dạng 2n + 1, còn các số nguyên tố là các số lớn hơn 1 chỉ chia hết cho 1 và cho chính nó.
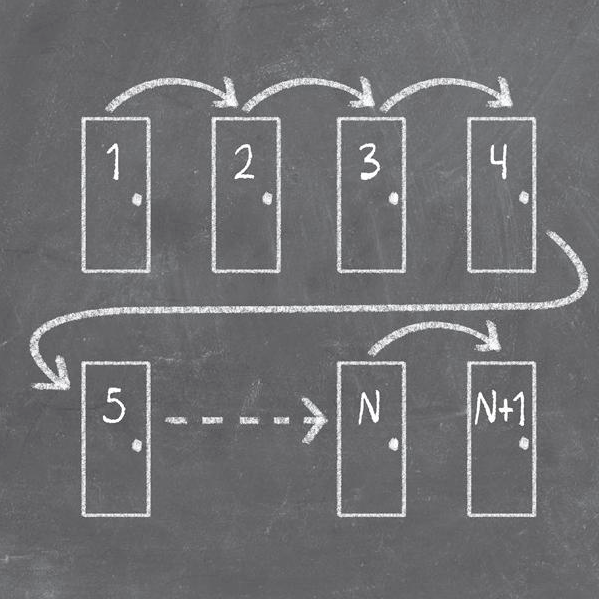
Các kiểu số khác nảy sinh tự nhiên trong toán học – ví dụ trong các số Fibonacci (1, 2, 3, 5, 8, 13, 21, 34,…), mỗi con số là tổng của hai số liền trước. Kiểu số này nảy sinh tự nhiên trong sinh học lẫn toán học. Các số Fibonacci còn liên hệ mật thiết với tỉ số vàng.
Các ví dụ khác bao gồm các bảng nhân, chúng được tạo ra bằng cách nhân các số nguyên dương với một con số nhất định, và các bình phương, trong đó mỗi con số là tích của một số tự nhiên với chính nó: n nhân n, hay n2, hay n bình phương.
Kết hợp các con số
Có vô số cách khác nhau để kết hợp hai con số cho trước bất kì. Chúng có thể được cộng với nhau để cho ra tổng của chúng, trừ cho nhau thành hiệu của chúng, nhân với nhau thành tích của chúng, và chia cho số chia khác zero để tạo thành thương của chúng. Quả vậy, nếu chúng ta nghĩ a – b là a + (-b) và a/b là a x (1/b), thì thật ra chỉ có các phép toán là cộng và nhân, cùng với phép nghịch đảo để tính 1/b.
Phép cộng và phép nhân được nói là có tính giao hoán, nghĩa là thứ tự các con số liên quan là không thành vấn đề, nhưng đối với những dãy tính phức tạp hơn thì trật tự tiến hành các phép tính có thể gây ra khác biệt. Để giúp làm rõ những trường hợp này, người ta phát triển những quy ước nhất định. Điều quan trọng nhất, các phép toán thực hiện trước được viết trong dấu ngoặc. Phép nhân và phép cộng còn thỏa mãn một số quy tắc tổng quát khác về cách chèn vào các dấu ngoặc, gọi là tính kết hợp và tính phân phối, như thể hiện trong ở trang sau.

TOÁN HỌC CẤP TỐC
Paul Glendinning | Bản dịch của Thuvienvatly.com
Phần tiếp theo >>