Benjamin Crowell
5.4 Điện thế đối với trường không đều
Bạn đọc am hiểu tính toán sẽ không gặp khó khăn gì trong việc khái quát mối quan hệ cường độ điện trường-hiệu điện thế cho trường hợp trường biến thiên. Thế năng liên quan đến một lực biến thiên là



o/ Hình bên trái: Bản đồ địa hình của vùng Stowe,Vermont. Độ cao chênh lệch từ đường đẳng mức này đến đường đẳng mức kế tiếp là 200 feet. Các đường càng cách xa nhau, như trong ngôi làng ở thấp hơn, cho thấy địa hình tương đối bằng phẳng, còn các đường càng gần nhau, giống như các đường ở phía tây thành phố chính, biểu diễn độ dốc nhảy bậc. Các dòng suối chảy từ trên đồi xuống, vuông góc với đường đẳng mức. Hình bên phải: Cũng bản đồ trên nhưng được vẽ lại có chiều sâu, với bóng đổ cho dễ nhìn.
5.5 Hai hoặc ba chiều
Bản đồ địa hình nêu trong hình o gợi ý một phương pháp tốt để hình dung mối liên hệ giữa điện trường và điện thế trong không gian hai chiều. Mỗi đường viền trên bản đồ là một đường đẳng mức; một vài trong số này được ghi rõ độ cao của chúng theo đơn vị feet. Chiều cao liên quan đến thế năng hấp dẫn, nên trong sự tương tự hấp dẫn, nên chúng ta có thể nghĩ chiều cao là biểu diễn cho điện thế. Ở nơi các đường viền cách xa nhau, như trong thành phố, độ dốc là thoai thoải. Các đường càng gần nhau cho thấy độ dốc càng lớn.
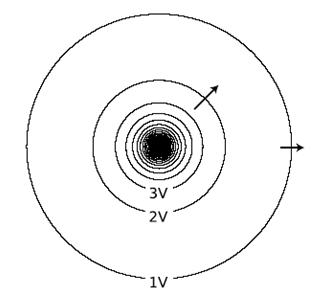
p/ Các đường cong đẳng thế xung quanh một điện tích điểm. Ở gần điện tích, các đường cong nằm sát nhau nên chúng nhập lại trong hình vẽ này do kích thước có hạn biểu diễn trên hình vẽ. Một số vectơ cường độ điện trường được chỉ rõ bằng mũi tên.
Nếu chúng ta đi dọc theo một đường thẳng, nói ví dụ như đi từ thành phố thẳng sang phía đông, thì chiều cao (điện thế) là một hàm của tọa độ x đông-tây. Sử dụng định nghĩa toán học thường dùng của độ dốc, và viết V cho chiều cao để nhắc nhở chúng ta sự tương tự điện, thì độ dốc dọc theo một đường như thế là DV/Dx. Nếu độ dốc không phải là một hằng số, chúng ta cần sử dụng độ dốc của đồ thị V-x, hoặc sử dụng phép tính và nói về đạo hàm dV/dx.
Nếu như mọi thứ không giới hạn theo một đường thẳng thì sao ? Nước chảy từ trên đồi xuống. Lưu ý cách thức các dòng suối trên bản đồ cắt vuông góc qua các đường đẳng mức.
Người ta có thể lập bản đồ điện thế theo kiểu tương tự, như chỉ rõ trong hình p. Điện trường mạnh nhất ở nơi các đường cong đẳng thế gần nhau nhất, và vectơ cường độ điện trường luôn hướng vuông góc với các đường đẳng thế.
Hình r biểu diễn một số ví dụ về cách thức hình dung hình ảnh trường và điện thế.
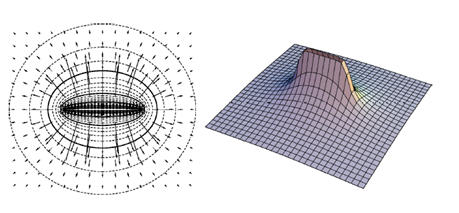
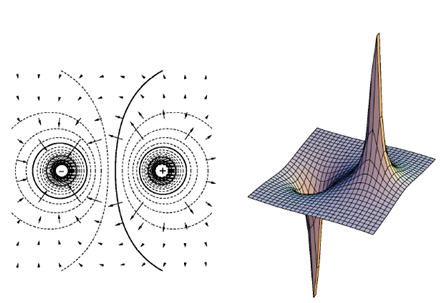
r/ Hình ảnh điện trường và điện thế hai chiều. Hình trên: Một thanh tích điện đều. Hình dưới: Một lưỡng cực. Trong mỗi trường hợp, biểu đồ ở bên trái biểu diễn các vectơ trường và đường cong đẳng thế, còn đồ thị bên phải biểu diễn điện thế (hệ tọa độ trên-dưới) là hàm của x và y. Chú thích các biểu đồ trường: Mỗi mũi tên biểu diễn trường tại điểm nơi ngọn của nó định vị. Để cho rõ ràng, một số mũi tên trong vùng cường độ điện trường rất mạnh không biểu diễn như trên, chúng quá dài nên vẽ ra được. Chú thích cho các đường cong đẳng thế: Trong những vùng điện trường rất mạnh, các đường cong không được chỉ rõ vì chúng nhập lại thành vùng đen đậm. Chú thích cho các đồ thị phối cảnh: Cần nhớ rằng mặc dù chúng ta hình dung các thứ trong không gian ba chiều, nhưng đây thật ra là biểu diễn điện thế hai chiều. Chiều thứ ba (trên-dưới) biểu diễn điện thế, chứ không phải vị trí.
Về mặt toán học, các phép tính của phần 5.4 khái quát hóa cho không gian ba chiều như sau:
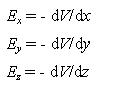
© Tưởng tượng rằng bản đồ địa hình trong hình q biểu diễn điện thế chứ không phải độ cao. (a) Xét dòng chảy bắt đầu ở gần chính giữa của bản đồ. Hãy xác định dấu dương và âm của dV/dx và dV/dy, và liên hệ chúng với hướng của lực đang đẩy dòng điện chạy về phía trước chống lại sức cản của ma sát. (b) Nếu bạn muốn tìm thật nhiều điện tích trên bản đồ này, thì bạn sẽ tìm ở chỗ nào ?
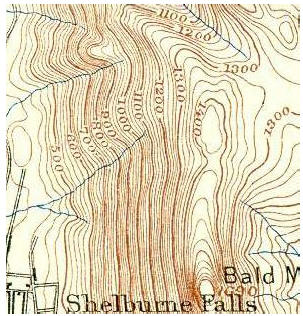
Hình q
5.6 Điện trường của sự phân bố điện tích liên tục
Điện tích thật sự xuất hiện thành những phần riêng biệt, nhưng thông thường để cho tiện lợi về mặt toán học, người ta xem tập hợp các điện tích như thể chúng giống như một dòng chất lưu liên tục trải ra trong một vùng không gian. Ví dụ, một quả cầu kim loại tích điện sẽ có điện tích trải ra gần như đồng đều trên toàn bộ bề mặt của nó, và trong đa số mục đích người ta thường bỏ qua thực tế là tính chất đều đặn này bị phá vỡ ở mức độ nguyên tử. Điện trường do một sự phân bố điện tích liên tục như thế gây ra là tổng các điện trường do từng phần của nó gây ra. Nếu chúng ta đặt các “phần” đó trở nên nhỏ tí xíu, thì chúng ta có tổng của một số vô hạn những số vô cùng nhỏ, tức là một tích phân. Nếu nó là một tổng rời rạc, thì chúng ta có điện trường tổng cộng theo hướng x là tổng của mọi thành phần x của từng trường riêng lẻ, và tương tự chúng ta sẽ có tổng cho các thành phần y và z. Trong trường hợp liên tục, chúng ta có ba tích phân.
Ví dụ 8. Điện trường của một thanh tích điện đều
Ñ Một thanh chiều dài L có điện tích Q trải đều dọc theo nó. Tìm điện trường tại điểm nằm cách chính giữa thanh một khoảng d, dọc theo trục của thanh.
Þ Đây là một tình huống một chiều, nên chúng ta thật ra chỉ cần tiến hành một phép tích phân biểu diễn điện trường tổng cộng dọc theo trục. Chúng ta tưởng tượng chia thanh ra thành những phần ngắn có chiều dài dz, mỗi phần có điện tích dq. Vì điện tích trải đều theo thanh, nên chúng ta có dq = ldz, trong đó l = Q/L là điện tích trên đơn vị chiều dài, có đơn vị coulom trên mét. Vì các phần chia vô cùng ngắn, nên chúng ta xem chúng là điện tích điểm và sử dụng biểu thức kdq/r2 cho sự đóng góp của chúng vào điện trường, trong đó r = d – z là khoảng cách tính từ điện tích tại z đến điểm mà chúng ta thích.
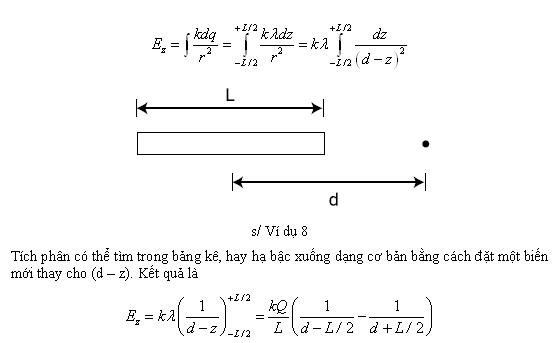
Đối với các giá trị lớn của d, biểu thức này cho giá trị nhỏ hơn vì hai nguyên do: (1) mẫu của phân thức trở nên lớn, và (2) hai phân thức trở nên gần như bằng nhau, và có xu hướng triệt tiêu nhau. Điều này có ý nghĩa, vì trường sẽ phải yếu hơn khi ta đi xa điện tích hơn. Trên thực tế, trường ở khoảng cách lớn phải tiến tới kQ/d2, vì từ một khoảng cách thật lớn, thanh trông như một điểm
Cũng thật hứng thú lưu ý rằng điện trường trở nên vô hạn ở hai đầu thanh, nhưng không vô hạn trên phần trong của thanh. Bạn có thể giải thích tại sao điều này xảy ra không ?
Trần Nghiêm dịch
Còn tiếp...