Benjamin Crowell
1.4 Lượng tử hóa điện tích
Chứng tỏ nguyên tử thật sự tồn tại là một mục tiêu lớn đã đạt, nhưng việc chứng minh sự tồn tại của chúng không giống với việc tìm hiểu những tính chất của chúng. Lưu ý các quan sát Brown-Einstein rốt cuộc chẳng có liên quan gì tới điện học cả, và cho tới đây chúng ta biết rằng vật chất vốn dĩ có tính chất điện, và chúng ta đã thành công trong việc giải thích những tính chất điện nhất định dưới hình thức các hạt mang điện dương và âm linh động. Những hạt này có phải là nguyên tử không ? Hay chúng là những bộ phận của nguyên tử ? Các hạt đó có hoàn toàn tách khỏi nguyên tử ? Có lẽ thật là quá sớm nếu như cố gắng trả lời những câu hỏi này mà không có bằng chứng thuyết phục ủng hộ mô hình hạt tích điện của điện học.
Bằng chứng ủng hộ mạnh mẽ cho mô hình hạt tích điện đến từ một thí nghiệm trong năm 1911 do nhà vật lí Robert Millikan thực hiện ở trường đại học Chicago. Hãy xét một dòng giọt nước hoa hoặc chất lỏng khác cho thổi qua một lỗ đinh ghim nhỏ xíu. Các giọt đi ra từ lỗ phải nhỏ hơn lỗ và thực tế thì chúng còn vi mô hơn nữa, vì dòng xoáy của không khí có xu hướng làm tản loạn chúng ra. Millikan lập luận rằng những giọt đó cần một chút điện tích khi chúng cọ xát lên thành lỗ mà chúng đi qua, và nếu mô hình hạt tích điện của điện học là đúng đắn, thì điện tích có thể tách vỡ trong số quá nhiều giọt chất lỏng nhỏ xíu nên một giọt có thể có lượng điện tích toàn phần thừa thải của một vài hạt tích điện – có lẽ là sự thừa thải của một hạt tích điện dương trên một giọt nhất định, hoặc sự thừa thải hai điện tích âm trên giọt khác.
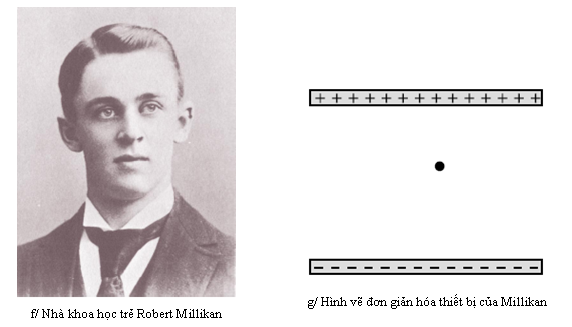
Thiết bị khéo léo của Millikan, g, gồm hai bản kim loại, chúng có khả năng tích điện khi cần thiết. Ông phun một đám giọt dầu vào không gian giữa hai bản, và chọn một giọt qua kính hiển vi để nghiên cứu. Ban đầu, khi không có điện tích trên các bản, ông xác định khối lượng của giọt bằng cách cho nó rơi trong không khí và đo vận tốc giới hạn của nó, tức là vận tốc ở đó lực ma sát của không khí triệt tiêu lực hấp dẫn. Lực kéo theo của không khí tác dụng lên một quả cầu chuyển động chậm đã được tìm ra bằng thực nghiệm là bvr2, trong đó b là một hằng số. Đặt lực toàn phần bằng không khi giọt chất lỏng rơi ở vận tốc giới hạn cho ta
bvr2 – mg = 0
và đặt tỉ trọng đã biết của dầu bằng với khối lượng của giọt chất lỏng chia cho thể tích của nó cho ta phương trình thứ hai

Mọi thứ trong những phương trình này có thể đo trực tiếp, ngoại trừ m và r, nên đây là hai phương trình hai ẩn, người ta có thể giải chúng để biết giọt chất lỏng lớn cỡ nào.
Sau đó, Millikan tích điện cho các bản kim loại, điều chỉnh lượng điện tích trung hòa chính xác với lực hấp dẫn và đẩy giọt chất lỏng nằm lơ lửng. Chẳng hạn, nếu giọt chất lỏng được làm cho có điện tích toàn phần là âm, thì điện tích dương đặt trên bản trên sẽ hút nó, kéo nó lên, và điện tích âm nằm trên bản dưới sẽ đẩy nó, nâng nó lên. (Về mặt lí thuyết chỉ cần một bản thôi, nhưng trên thực tế sự sắp xếp hai bản như thế này cho lực điện có độ lớn đều hơn trong toàn vùng không gian giọt chất lỏng rơi) Lượng điện tích trên hai bản cần thiết cho giọt dầu lơ lửng cho Millikan một cơ sở xác định lượng điện tích giọt chất lỏng mang. Điện tích giọt chất lỏng mang càng lớn, thì lực điện tác dụng lên nó sẽ càng mạnh, và thủ thuật là phải đặt điện tích trên các bản nhỏ thôi. Thật không may, việc biểu diễn mối quan hệ này bằng định luật Coulomb sẽ không thực tế, vì nó cần sự hiểu biết trọn vẹn về việc điện tích phân bố như thế nào trên mỗi bản, cùng với khả năng thực hiện phép cộng vectơ của tất cả các lực tác dụng lên giọt chất lỏng bởi tất cả các điện tích trên bản. Thay vì vậy, Millikan sử dụng một cơ sở thực tế là lực điện mà một điện tích điểm chịu tại một điểm trong không gian tỉ lệ với điện tích của nó
F/q = const
Với lượng điện tích cho trước trên các bản, hằng số này có thể được xác định chẳng hạn bằng cách vứt bỏ giọt dầu đi, xen giữa hai bản một vật lớn hơn và dễ cầm nắm hơn có một điện tích đã biết trên nó, và đo lực với phương pháp thông thường. (Thật ra, Millikan sử dụng một bộ kĩ thuật hơi khác để xác định hằng số đó, nhưng ý tưởng cũng tương tự) Độ lớn của lực tác dụng lên giọt dầu thực tế phải bằng mg, vì lực chỉ vừa đủ để nâng bổng nó lên, và một khi hằng số định cỡ đã được xác định, thì điện tích của giọt chất lỏng khi đó có thể tìm ra được dựa trên khối lượng đã xác định trước đó của nó.

Bảng h cho một vài kết quả từ bài báo năm 1911 của Millikan. (Millikan xử lí dữ liệu trên cả những giọt tích điện âm và dương, nhưng trong bài báo của ông, ông chỉ mang ra ví dụ dữ liệu về những giọt tích điện âm, nên ở đây toàn là số âm) Chỉ cần liếc qua số liệu trên cũng thấy ngay rằng điện tích không đơn giản là một loạt số ngẫu nhiên. Chẳng hạn, điện tích thứ hai hầu như chính xác bằng phân nửa điện tích thứ nhất. Millikan giải thích điện tích quan sát được đều là bội số nguyên của một con số đơn giản, 1,64 x 10-19 C. Trong cột thứ hai, lấy điện tích chia cho hằng số này được kết quả về cơ bản là số nguyên, cho phép sai lệch ngẫu nhiên có mặt trong thí nghiệm. Millikan phát biểu trong bài báo của ông rằng những kết quả này là
… bằng chứng trực tiếp và xác thực… của sự đúng đắn của quan điểm đã được cải tiến trong nhiều năm qua và được củng cố bởi bằng chứng từ nhiều nguồn cho thấy mọi điện tích, là những bội số chính xác của một điện tích cơ bản, hữu hạn, hay nói cách khác, một điện tích rải đều trên bề mặt tích điện có một cấu trúc dạng hạt hữu hạn, trên thực tế, gồm những hạt nhỏ, hay những nguyên tử điện, tất cả đều giống hệt nhau, rắc trên bề mặt của vật mang điện.
Nói cách khác, ông đã cung cấp bằng chứng trực tiếp cho mô hình hạt tích điện của điện học và bác bỏ những mô hình trong đó mô tả điện là một số loại chất lỏng. Điện tích cơ bản được kí hiệu là e, và giá trị hiện nay là 1,60 x 10-19 C. Từ “lượng tử hóa” được sử dụng trong vật lí để mô tả một đại lượng chỉ có thể có những giá trị số nhất định, và không thể có bất kì giá trị nào nằm giữa những giá trị đó. Theo cách hiểu này, chúng ta nói rằng Millikan đã phát hiện điện tích bị lượng tử hóa. Điện tích e thường được gọi là lượng tử điện tích.
¤ Tiền tệ có bị lượng tử hóa ? Lượng tử của tiền tệ là gì ?
Ghi chép lịch sử về trò gian lận của Millikan
Rất ít sách giáo khoa vật lí phổ thông đề cập đến thực tế rõ ràng rằng mặc dù những kết luận của Millikan là đúng đắn, nhưng ông là một kẻ gian lận khoa học. Kĩ thuật của ông khó và đòi hỏi phải thật cẩn thận khi thực hiện, và sổ sách ghi chép nguyên bản của ông, đến nay vẫn còn giữ được, cho thấy số liệu kém hoàn hảo hơn nhiều so với như ông khẳng định trong những bài báo khoa học đã công bố của ông. Trong những ấn phẩm này, ông phát biểu thẳng thừng rằng mỗi giọt dầu quan sát có điện tích là một bội số của e, với không có ngoại lệ và sai sót nào. Nhưng sổ ghi chép của ông có thừa những ghi chú đại loại như “số liệu đẹp, giữ” và “tệ quá, bỏ đi”. Sau đó, Millikan đã giành giải thưởng Nobel vật lí cho sự mô tả không trung thực về số liệu của ông.
Tại sao các tác giả sách giáo khoa quên không nói tới trò gian lận của Millikan ? Hình như họ nghĩ rằng học sinh, sinh viên còn quá ngây thơ để đánh giá chính xác ngụ ý của thực tế rằng đôi khi vẫn tồn tại những trò gian trá khoa học và thậm chí còn được trao giải thưởng của những tổ chức khoa học. Có lẽ họ e ngại sinh viên sẽ làm qua loa số liệu gian trá cho xong, vì Millikan đoạt giải Nobel cũng bằng cách đó mà. Nhưng xuyên tạc lịch sử không hơn gì là mỉa mai. Chẳng phải các thầy giáo người Anh đã cải biên bi bịch của Sheakspeare sao cho nhân vật xấu luôn luôn bị đối xử thậm tệ, còn nhân vật tốt thì chưa bao giờ bị đối xử như thế đó hay sao !
Một lời giải thích khả dĩ khác đơn giản là thiếu căn cứ; có khả năng là một số giáo trình có tiếng không muốn phê phán trò bịp của Millikan và những tác giả sau đó cũng xử sự như thế. Nhà sinh vật học Stephen Jay Gould đã viết một bài tiểu luận vạch ra một ví dụ chỉ rõ các tác giả sách giáo khoa sinh học có xu hướng đi theo cách xử lí truyền thống của một chủ đề, sử dụng cái cổ của con hươu cao cổ để bàn về tính không kế thừa của những đặc điểm cần thiết. Lúc ấy, một lời giải thích khác là các nhà khoa học có được địa vị từ hình ảnh trước công chúng của họ là những người tìm kiếm sự thật một cách vô tư, và họ không muốn công chúng nhận ra bản chất con người và không hoàn hảo của họ. (Chính Millikan là một nhà cải cách giáo dục, và ông đã viết một loạt sách giáo khoa có chất lượng cao hơn nhiều so với trước thời kì của ông).
Ghi chú thêm vào tháng 9/2002
Vài năm sau khi tôi viết câu chuyện lịch sử ngoài lề này, tôi đã bắt gặp một sự bênh vực lí thú cho Millikan từ phía David Goodstein (American Scientist, Jan-Feb 2001, trang 54-60). Goodstein biện hộ rằng mặc dù Millikan đã viết một câu dối trá trong bài báo của ông, nhưng Millikan không đáng trách là kẻ lừa dối khi ông đưa câu đó vào trong ngữ cảnh. Millikan phát biểu rằng ông chưa bao giờ vứt đi bất kì số liệu nào, và ông thật sự đã vứt bỏ số liệu, nhưng ông có lí do chính đáng, khách quan cho việc loại bỏ số liệu đó. Vấn đề Millikan có thể vẫn gây tranh cãi trong số các nhà sử học, nhưng ở đây tôi sẽ rút ra hai bài học:
- Tình tiết đó có thể làm giảm sự tín cẩn của chúng ta vào Millikan, nhưng nó làm tăng thêm niềm tin của chúng ta vào khoa học. Kết quả đúng đắn cuối cùng sẽ được công nhận, chứ không thể như trong lĩnh vực giả khoa học giống như y học.
- Trong khoa học, sự tùy tiện cũng tồi tệ như trò lừa bịp cờ gian bạc lận. Nếu khoa học biết đôi điều về sự thật tuyệt đối, thì nó sẽ không cần lí do gì để giải thích cả.
Còn tiếp...
Xem lại Phần 3