Khách sạn Hilbert
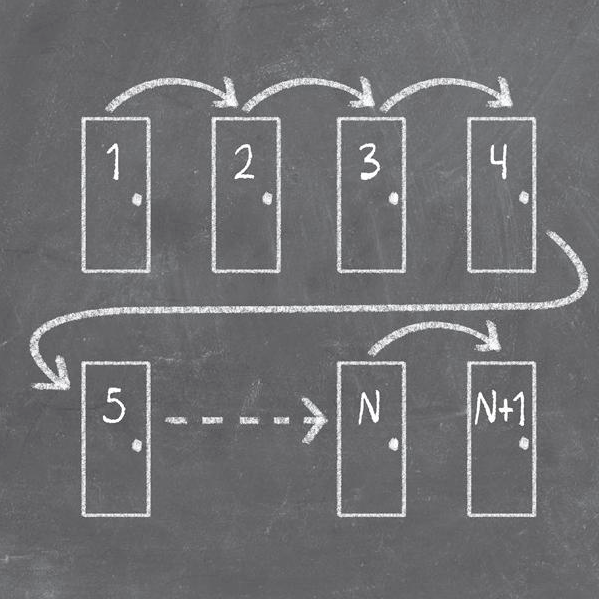
Khách sạn Hilbert là một suy diễn do nhà toán học David Hilbert phát minh ra để hình dung ý tưởng kì lạ về những vô hạn đếm được. Khách sạn tưởng tượng này có một tập hợp phòng vô hạn đếm được mang số thứ tự 1, 2, 3,… và đều đã đầy người, khi một người đến muộn và khẩn khoản xin một phòng.
Sau một lát suy nghĩ, người quản lí sử dụng một hệ thống thông tin nội bộ yêu cầu mỗi người khách di chuyển sang phòng tiếp theo theo trình tự số. Vậy nên người ở phòng 1 chuyển sang phòng 2, phòng 2 chuyển sang phòng 3, và cứ thế. Với mỗi vô hạn khách đếm được ở phòng N, luôn luôn có phòng N + 1 cho họ chuyển sang, thành ra vào lúc mọi người di chuyển, phòng 1 còn trống cho vị khách mới vào ở.
Khách sạn Hilber cho thấy rằng kết quả của việc thêm một phần tử vào một tập hợp vô hạn đếm được vẫn là một tập hợp đếm được, vì thế phải có những vô hạn đếm được khác nhau.
Đếm số hữu tỉ
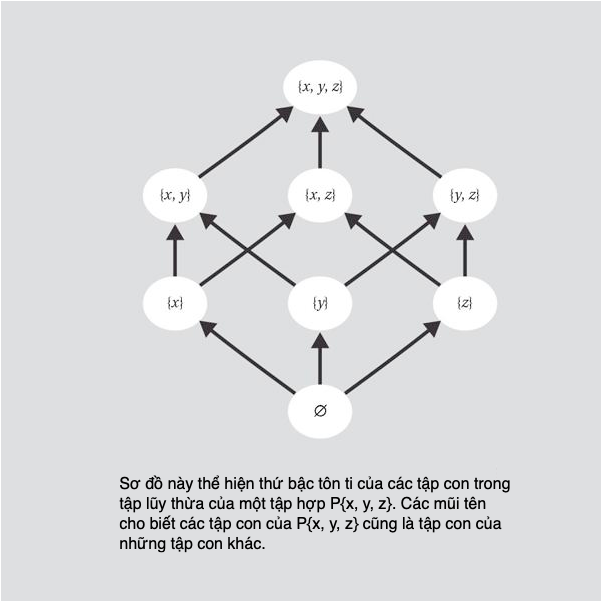
Mặc dù không phải mọi tập hợp hữu hạn đều đếm được, nhưng một số tập hợp (đếm được) thật sự rất lớn. Trong số này bao gồm số hữu tỉ - các số được lập từ tỉ số của hai số nguyên, a/b. Ta có thể chứng minh điều này bằng cách chỉ nhìn vào các số hữu tỉ giữa 0 và 1.
Giả sử các số hữu tỉ giữa 0 và 1 là đếm được, thì chúng ta sẽ có thể đặt chúng vào một trật tự tạo thành một danh sách hoàn chỉnh, dù là vô hạn. Trật tự tăng dần của cỡ độ lớn chẳng ích lợi gì ở đây bởi vì giữa hai số hữu tỉ bất kì người ta luôn có thể tìm thấy một số khác, vì thế thậm chí chúng ta không thể viết ra phần tử đầu tiên và thứ hai của một danh sách như thế. Thế liệu có cách nào khác liệt kê các con số hay không?
Một giải pháp là xếp trật tự các con số theo mẫu số, b, của chúng trước, sau đó đến tử số, a, của chúng, như ở trang sau. Ở phương pháp này có một sự lặp lại, nhưng mỗi số hữu tỉ giữa 0 và 1 sẽ xuất hiện ít nhất một lần trong danh sách.
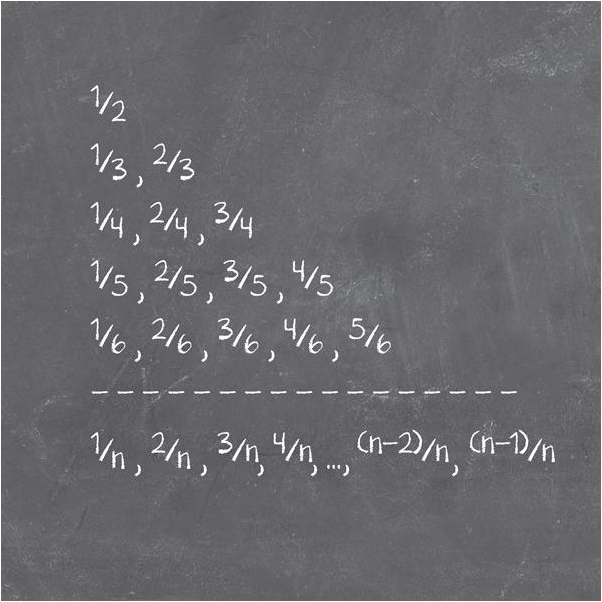
TOÁN HỌC CẤP TỐC
Paul Glendinning | Bản dịch của Thuvienvatly.com