i
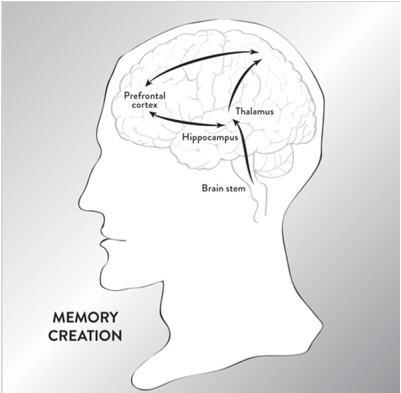
i là một “con số” dùng để biểu diễn căn bậc hai của – 1. Khái niệm này không thật sự là một con số theo nghĩa đếm được, và được gọi là số ảo. Khái niệm i hữu ích khi chúng ta cố giải một phương trình như x2 + 1 = 0, nó có thể được sắp xếp lại là x2 = –1. Vì bình phương một số thực dương hay âm bất kì đều cho kết quả dương, nên phương trình này không có nghiệm thực. Thế nhưng trong một ví dụ kinh điển về nét đẹp và tiện ích của toán học, nếu chúng ta định nghĩa một nghiệm và đặt cho nó một cái tên (i), thì ta có thể đi tới một mở rộng phù hợp hoàn hảo với số thực. Y hệt như các số dương vừa có một căn bậc hai dương và một căn bậc hai âm, –i cũng là căn bậc hai của –1, và phương trình x2 + 1 = 0 có hai nghiệm.
Được trang bị số ảo mới này, một thế giới mới của các số phức, vừa có phần thực vừa có phần ảo, mở ra trước mắt chúng ta.
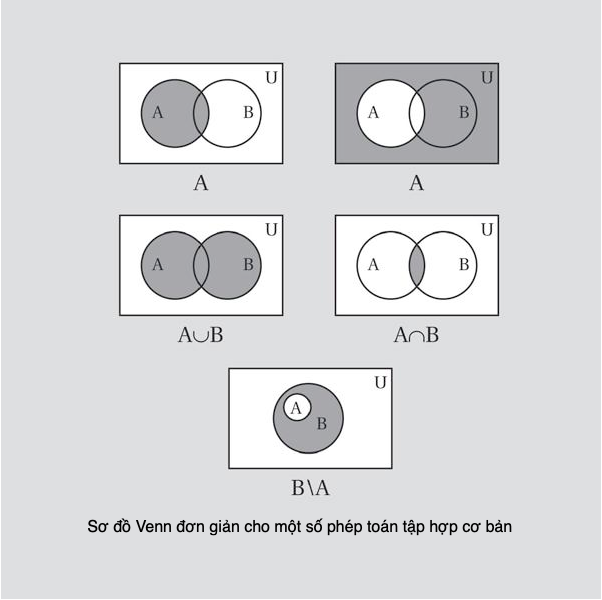
Tập hợp
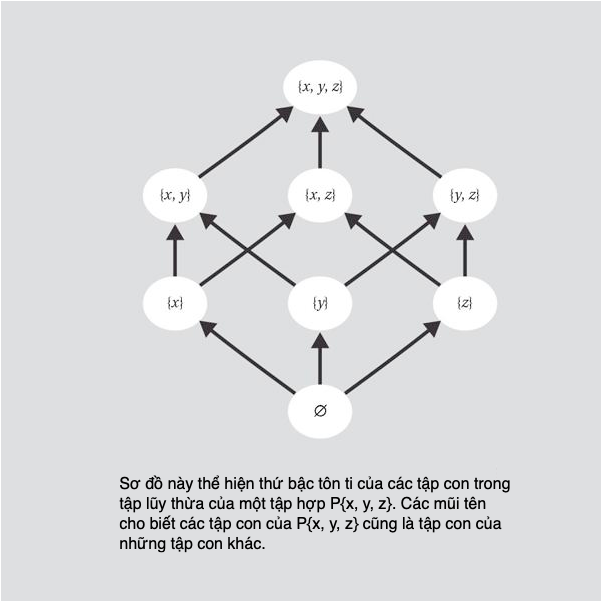
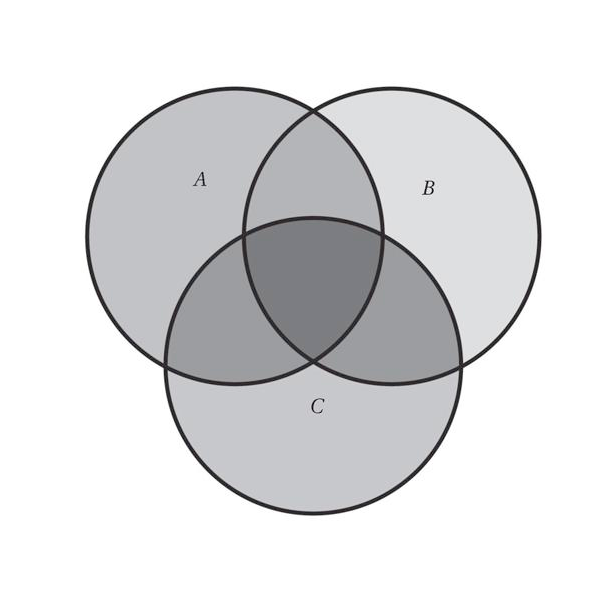
Một tập hợp đơn giản là một bộ sưu tập các đối tượng. Các đối tượng trong một tập hợp được gọi là các phần tử của nó. Ý tưởng về tập hợp có sức mạnh rất lớn, và ở nhiều phương diện các tập hợp chính là các viên gạch cấu trúc tuyệt đối cơ bản của toán học – còn cơ bản hơn các con số.
Một tập hợp có thể có hữu hạn hoặc vô hạn phần tử, và thường được mô tả bằng cách khoanh kín các phần tử trong cặp ngoặc nhọn íý. Trật tự viết các phần tử không quan trọng trong việc định danh tập hợp, nếu một phần tử bị lặp lại cũng chẳng sao. Các tập hợp cũng có thể được lập ra từ những tập hợp khác, tuy nhiên chúng ta phải mô tả chúng cho thật kĩ.
Một lí do khiến các tập hợp hữu dụng như thế là vì chúng cho phép chúng ta giữ được cái chung chung, không phải quan tâm đến cấu trúc của từng đối tượng được nghiên cứu. Các phần tử trong một tập hợp có thể là bất kì thứ gì từ các con số cho đến người ta đến các hành tinh, hoặc lộn xộn cả ba thứ này, mặc dù trong các ứng dụng thì thông thường các phần tử có liên quan với nhau.
TOÁN HỌC CẤP TỐC
Paul Glendinning | Bản dịch của Thuvienvatly.com
