CHƯƠNG 4
KHÔNG-THỜI GIAN
Trong các chương trước, ta đã dõi theo con đường lịch sử đưa đến thuyết tương đối, và thực tế luận giải của chúng tôi không cách biệt lắm với cái Einstein trình bày lúc ban đầu. Ta buộc phải chấp nhận rằng không gian chẳng phải là một vũ đài vĩ đại mà trên đó các sự kiện cuộc sống của chúng ta trình diễn nữa. Tương tự, thời gian chẳng phải là cái gì đó phổ quát và tuyệt đối. Thay vậy, ta đã chuyển sang một bức tranh không gian và thời gian dát mỏng được và mang tính chủ quan hơn nhiều. Chiếc đồng hồ vĩ đại trên bầu trời, và hiểu theo một nghĩa nào đó là bản thân bầu trời, đã bị vứt bỏ. Ta có cảm giác như thế giới là một cái hộp trong đó chúng ta đi lại làm ăn, bởi vì bức tranh đó cho phép chúng ta hình dung thế giới nhanh chóng và hiệu quả. Khả năng lập bản đồ chuyển động của các thứ trên một mạng lưới tưởng tượng là cái ta gọi là nhận thức không gian, và nó rõ ràng quan trọng nếu bạn né tránh thú săn mồi, tìm kiếm thức ăn và sống sót trong một môi trường nguy hiểm và đầy thử thách. Nhưng chẳng có lí do gì tại sao mô hình này, chôn sâu bên trong bộ não của chúng ta và được củng cố trên hàng triệu năm bởi sự chọn lọc tự nhiên, phải là cái gì đó chứ không phải một mô hình. Nếu một cách suy nghĩ về thế giới mang lại một lợi thế sống còn, thì cách suy nghĩ đó sẽ trở nên phổ biến. Tính chính xác khoa học của nó là không có liên quan. Điều quan trọng là, bởi vì chúng ta chọn chấp nhận các kết quả thí nghiệm diễn ra trên bàn làm việc lốm đốm của Faraday và các lí giải mà Maxwell đã hệ thống hóa, nên chúng ta hành động giống như các nhà khoa học và bác bỏ mô hình dễ chịu của không gian và thời gian đã cho phép tổ tiên của chúng ta sống sót và phồn thịnh trên các đồng bằng cổ ở châu Phi. Mô hình này được khắc ghi và gia cố sâu trong tâm khảm của chúng ta bởi kinh nghiệm của chúng ta trong nhiều triệu năm trời, và việc bác bỏ nó có thể gây mất phương hướng. Cảm giác mơ hồ hỗn loạn đó, nếu (hi vọng) sau đó là sự xuất hiện của cái rõ ràng, là niềm vui thú của khoa học. Nếu quý độc giả cảm thấy hoang mang, thì chúng tôi hi vọng sẽ mang lại cho các bạn niềm vui thú vào cuối quyển sách này.
Đây không phải là sách lịch sử. Mục tiêu của chúng tôi là mô tả không gian và thời gian theo cách tường minh nhất mà chúng tôi có thể, và quan điểm của chúng tôi là tiến trình lịch sử đưa đến thuyết tương đối không nhất là lộ trình tốt nhất để khai sáng. Từ bối cảnh hiện đại, hơn một thế kỉ sau cuộc cách mạng của Einstein, ta đã học được rằng có một cách sâu sắc hơn và dễ chịu hơn để nghĩ về không gian và thời gian. Thay vì đào sâu hơn vào quan điểm giáo khoa kiểu cũ, chúng ta sẽ bắt đầu lại từ khoảng vườn trống. Khi làm như vậy ta sẽ hiểu được cái Minkowski muốn nói khi ông phát biểu rằng không gian và thời gian phải hợp nhất thành một thực thể. Một khi phát triển được một bức tranh tươi đẹp hơn, ta sẽ sẵn sàng đạt tới mục tiêu chính của chúng tôi – ta sẽ có thể suy luận ra công thức E = mc2.
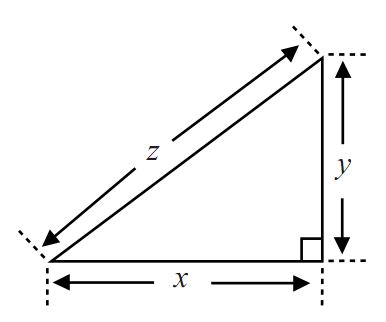
Đây là điểm xuất phát. Các lí thuyết của Einstein có thể được xây dựng gần như hoàn toàn bằng ngôn ngữ hình học. Nghĩa là, bạn không cần biết nhiều đại số, chỉ cần hình ảnh và các khái niệm. Tọa lạc tại trung tâm của lí thuyết chỉ có ba khái niệm: bất biến, nhân quả, và khoảng cách. Trừ khi bạn là nhà vật lí, chứ hai trong ba khái niệm trên có lẽ là những từ ít quen thuộc, từ thứ ba thì quen thuộc nhưng, như ta sẽ thấy, nó tinh tế hơn.
Bất biến là một khái niệm trọng điểm của vật lí hiện đại. Hãy gấp quyển sách này lại và nhìn ra thế giới bên ngoài nào. Bây giờ hãy xoay người và nhìn về hướng ngược lại. Căn phòng của bạn sẽ trông khác nhau từ những góc nhìn khác nhau, tất nhiên rồi, nhưng các định luật của tự nhiên thì giống nhau. Cho dù bạn đang hướng về phía bắc, nam, đông hoặc tây, thì lực hấp dẫn vẫn có cùng độ lớn và vẫn giữ chân của bạn bám trên đất. Ti vi của bạn vẫn hoạt động khi bạn xoay nó vòng vòng, và xe hơi của bạn vẫn khởi động cho dù bạn đỗ nó ở London, Los Angeles hay Tokyo. Đây là các thí dụ của sự bất biến trong tự nhiên. Khi đặt ra như vậy, sự bất biến trông có chút giống với một phát biểu rõ ràng. Nhưng việc áp dụng yêu cầu bất biến cho các lí thuyết khoa học của chúng ta tỏ ra là một việc làm hết sức hữu ích. Ta vừa mô tả hai dạng khác nhau của bất biến. Yêu cầu rằng các định luật của tự nhiên sẽ không thay đổi nếu chúng ta xoay vòng quanh và xác định chúng trong khi nhìn về những hướng khác nhau được gọi là bất biến quay. Yêu cầu rằng các định luật sẽ không thay đổi nếu ta di chuyển từ nơi này sang nơi khác được gọi là bất biến tịnh tiến. Những yêu cầu có vẻ tầm thường này hóa ra lại hết sức quyền năng trong tay của Emmy Noether, người được Albert Einstein mô tả là người phụ nữ quan trọng nhất trong lịch sử toán học. Vào năm 1918, Noether công bố một định lí làm sáng tỏ một liên hệ sâu sắc giữa sự bất biến và sự bảo toàn của những đại lượng vật lí nhất định. Ta sẽ còn nói nhiều hơn về các định luật bảo toàn trong vật lí học ở phần sau, còn lúc này ta chỉ cần phát biểu kết quả sâu sắc mà Noether đã khám phá. Trong thí dụ đặc biệt nhìn vào thế giới theo những hướng khác nhau, nếu các định luật của tự nhiên vẫn không thay đổi bất chấp hướng ta đang nhìn, thì có tồn tại một đại lượng được bảo toàn. Trong trường hợp này, đại lượng được bảo toàn được gọi là moment động lượng. Trong trường hợp bất biến tịnh tiến, đại lượng được bảo toàn là động lượng. Tại sao điều này lại quan trọng? Hãy lấy một thực tế vật lí ra khỏi chiếc mũ ẩn dụ và giải thích nó.
Mặt trăng di chuyển 4 cm ra xa Trái đất mỗi năm. Tại sao ư? Hãy hình dung Mặt trăng trong con mắt trí tuệ của bạn là đang đứng yên phía trên bề mặt Trái đất đang quay tròn. Nước trong các đại dương nằm ngay bên dưới Mặt trăng sẽ nhô lên một chút về phía Mặt trăng bởi vì lực hấp dẫn của Mặt trăng đang hút nó, và Trái đất sẽ quay một vòng mỗi ngày bên dưới chỗ nhô này. Đây là nguyên nhân của thủy triều. Có lực ma sát giữa nước và bề mặt Trái đất, và lực ma sát này làm cho tốc độ quay của Trái đất chậm dần. Hiệu ứng hết sức nhỏ nhưng có thể đo được; ngày trên Trái đất đang từ từ dài ra xấp xỉ hai phần nghìn của một giây trên mỗi thế kỉ. Các nhà vật lí đo tốc độ quay bằng moment động lượng, vì thế ta có thể nói moment động lượng của Trái đất đang giảm theo thời gian. Noether cho chúng ta biết rằng vì thế giới trông giống nhau theo mọi hướng (hay nói chính xác hơn, các định luật của tự nhiên là bất biến dưới chuyển động quay), nên moment động lượng được bảo toàn, nghĩa là tổng lượng chuyển động quay phải không thay đổi. Vậy cái gì xảy ra với moment động lượng mà Trái đất mất mát bởi ma sát thủy triều? Câu trả lời là nó được truyền cho Mặt trăng, làm nó tăng tốc độ trong quỹ đạo quay xung quanh Trái đất để bù cho sự chậm lại của chuyển động quay của Trái đất. Như vậy khiến nó hơi bị lệch ra xa Trái đất. Nói cách khác, để đảm bảo rằng moment động lượng toàn phần của hệ Trái đất và Mặt trăng được bảo toàn, Mặt trăng phải giạt vào một quỹ đạo rộng hơn xung quanh Trái đất để bù cho thực tế tốc độ quay của Trái đất đang chậm lại. Đây là một hiệu ứng rất thực tế và khá kì lạ. Mặt trăng to lớn, và nó đang trôi giạt ra xa Trái đất khi mỗi năm trôi qua để bảo toàn moment động lượng. Tiểu thuyết gia người Ý Italo Calvino cảm thấy điều đó tuyệt vời đến mức ông đã viết một truyện ngắn tiêu đề “Khoảng cách đến Mặt trăng” trong đó ông tưởng tượng một thời đại trong quá khứ xa xăm khi tổ tiên của chúng ta có thể căng buồm hằng đêm trên những con tàu trên đại dương để thấy Mặt trăng lặn và dùng thang leo lên bề mặt của nó. Khi Mặt trăng trôi giạt ra xa theo năm tháng, rồi đến một đêm khi những người yêu trăng phải quyết định chọn lựa giữa việc bị kẹt lại trên Mặt trăng mãi mãi, hoặc quay trở lại Trái đất. Hiện tượng bất ngờ và lãng mạn này, dưới ngòi bút của Calvino, có lời giải thích của nó nằm ở khái niệm trừu tượng bất biến và mối liên hệ sâu sắc giữa sự bất biến và sự bảo toàn các đại lượng vật lí.

<< Phần trước | Phần tiếp theo >>