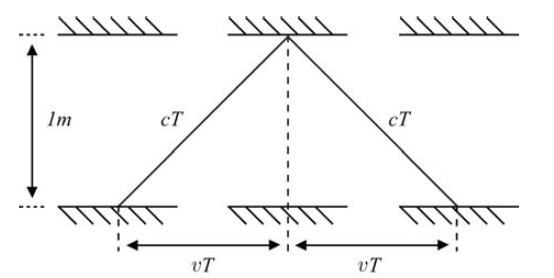
Để thiết kế một thí nghiệm như vậy, trước tiên ta cần tính toán xem một vật phải chuyển động nhanh bao nhiêu thì mới làm lộ ra hiệu ứng đã đề xuất. Cái khá rõ ràng là ngồi vào xe hơi lái 70 dặm/giờ trên đường cao tốc không làm cho thời gian trôi chậm lại nhiều lắm, bởi vì sau chuyến đi trở về nhà ta đâu có thấy con cái của mình đã trưởng thành và già hơn ta trong lúc ta đi xa. Điều này nghe thật ngớ ngẩn, nhưng cái giá trị của Einstein nằm ở chỗ đây là cái thật sự xảy ra, và chúng ta chắc chắn để ý thấy sự khác biệt chỉ nếu chúng ta có thể lái xe đủ nhanh. Vậy thế nào là đủ nhanh? Từ góc nhìn của người trên sân ga, ánh sáng truyền theo hai cạnh của tam giác được vẽ trên hình. Lập luận của Einstein là bởi vì ánh sáng phải truyền đi quãng đường lớn hơn so với nếu đồng hồ đứng yên, nên thời gian phải trôi qua chậm hơn, bởi vì tiếng tíc kéo dài hơn. Toàn bộ những gì ta phải làm bây giờ là tính xem tiếng tíc đó dài hơn bao nhiêu (với tốc độ đoàn tàu đã biết) và ta có câu trả lời. Ta có thể làm yêu cầu này với một chút giúp đỡ từ Pythagoras.
Hình 2
Nếu bạn không muốn theo dõi chi tiết tính toán thì bạn có thể bỏ qua các đoạn tiếp theo, nhưng sau đó bạn phải chấp nhận những kết quả tính toán của nó. Tính toán là chuyện không thể tránh khỏi để câu chuyện của chúng ta tiếp diễn. Tuy nhiên, luôn luôn có sự lựa chọn cho bạn là bỏ qua nó và không cần lo lắng gì cả - toán học giúp người ta nhận thức sâu hơn vật lí học chứ nó không tuyệt đối cần thiết để đọc tiếp quyển sách này. Hi vọng của chúng tôi là bạn sẽ dạo qua phần tính toán, mặc dù bạn chẳng có chút kinh nghiệm gì trước đây cả. Chúng tôi đã cố gắng giữ cho mọi thứ dễ hiểu. Có lẽ cách tốt nhất để sờ tới toán học là đừng lo lắng gì về nó. Những câu đố lôgic xuất hiện trên báo chí hàng ngày còn khó hơn những cái chúng ta sẽ làm trong quyển sách này. Tóm lại, ở đây có một trong những thủ thuật toán học khéo léo của quyển sách, nhưng kết quả đáng để ta nỗ lực.
Hãy nhìn vào Hình 2 một lần nữa và giả sử thời gian cho một nửa tiếng tíc của đồng hồ trên đoàn tàu được người trên sân ga đo bằng T. Đó là thời gian cho ánh sáng đi từ gương dưới lên gương trên. Mục tiêu của chúng ta là tính xem T thật sự bằng bao nhiêu và nhân đôi nó lên để có thời gian cho một tiếng tíc của đồng hồ theo người trên sân ga. Nếu ta đã biết T, thì ta có thể tính ra chiều dài của cạnh dài nhất của tam giác (cạnh huyền) là bằng cT, tức là bằng tốc độ ánh sáng, c, nhân với thời gian cần thiết cho ánh sáng đi từ gương dưới lên gương trên, T. Hãy nhớ rằng quãng đường bằng tốc độ nhân với thời gian đi hết quãng đường đó. Ví dụ, quãng đường mà một xe hơi đi trong một giờ với tốc độ 60 dặm/giờ là 60 × 1 = 60 dặm. Chẳng khó khăn gì để tính ra kết quả cho quãng đường đi trong hai giờ. Cái ta đang làm ở đây là viện dẫn công thức “quãng đường = tốc độ × thời gian”. Biết được T, ta còn tính được đồng hồ đã di chuyển bao xa trong nửa tiếng tíc. Nếu đồng hồ đang chuyển động ở một tốc độ, v, thì đồng hồ dịch chuyển được quãng đường vT trong mỗi nửa tiếng tíc. Một lần nữa ta chẳng làm gì khác ngoài việc sử dụng “quãng đường = tốc độ × thời gian”. Quãng đường này là độ dài cạnh đáy của một tam giác vuông và bởi vì ta biết độ dài của cạnh dài nhất, cho nên ta có thể tiếp tục và tính ra khoảng cách giữa hai gương bằng định lí Pythagoras. Nhưng ta biết khoảng cách đó là đã cho – nó bằng 1 mét. Vì thế, định lí Pythagoras cho ta biết rằng (cT)2 = 12 + (vT)2. Lưu ý công dụng của dấu ngoặc. Trong toán học, chúng được sử dụng để cho biết những toán tử nào được ưu tiên trước. Trong trường hợp này, (vT)2 có nghĩa là “nhân v với T và sau đó bình phương đáp số”. Thế là xong.
Lúc này ta đã gần như xong việc. Ta biết c, tốc độ ánh sáng, và giả sử ta biết tốc độ của đoàn tàu, v. Khi đó ta có thể sử dụng phương trình này để tính T. Cách thô thiển nhất là dự đoán một giá trị của T và xem nó có thỏa mãn phương trình không. Thường thì dự đoán sẽ sai và ta sẽ phải thử đoán lại. Sau một hồi ta có thể rút ra được đáp số đúng. May thay, ta có thể tránh được quá trình chán ngắt đó bởi vì phương trình trên là “giải được”. Đáp số là T2 = 1/(c2 – v2), nghĩa là “trước tiên tính c2 – v2 rồi lấy 1 đem chia cho số đó”. Dấu gạch chéo nghiêng về bên phải là kí tự ta sẽ dùng để kí hiệu “chia cho”. Vậy 1/2 = 0,5 và a/b nghĩa là “a chia cho b”, vân vân. Nếu bạn biết chút ít toán học, thì có lẽ bây giờ bạn cảm thấy hơi chán nhỉ. Nếu không, thì bạn có thể tự hỏi không biết làm sao ta có được T2 = 1/(c2 – v2). Vâng, đây không phải là một quyển sách toán, và bạn chỉ việc tin rằng chúng tôi làm toán đúng – bạn có thể luôn luôn tự thuyết phục mình rằng chúng tôi đúng bằng cách tự thay số vào. Thật vậy, ta đã có kết quả cho T2, nghĩa là “T nhân với T”. Ta rút ra T bằng cách lấy căn bậc hai. Về mặt toán học, căn bậc hai của một số là sao cho khi nhân số đó với chính nó ta thu về số ban đầu; ví dụ, căn bậc hai của 9 là 3, và căn bậc hai của 7 gần bằng 2,646. Có một nút nhấn trên đa số máy tính bỏ túi tính căn bậc hai giùm bạn. Nó thường được kí hiệu bởi kí tự “√” và người ta thường viết như thế này 3 = √9. Như bạn có thể thấy, căn bậc hai là ngược lại với bình phương, 42 = 16 và √16 = 4.
Trở lại với nhiệm vụ trong tay nào, bây giờ ta có thể viết thời gian cần thiết cho một tiếng tíc của đồng hồ được xác định bởi ai đó trên sân ga: Đó là thời gian cho ánh sáng đi lên gương trên và trở lại gương dưới – nghĩa là bằng 2T. Lấy căn bậc hai phương trình trên của chúng ta cho T2, rồi nhân với 2 ta được 2T = 2/√(c2 – v2). Phương trình này cho phép ta tính được thời gian cần thiết cho một tiếng tíc được đo bởi người trên sân ga, cho biết tốc độ của đoàn tàu, tốc độ ánh sáng, và khoảng cách giữa hai gương (1 mét). Còn thời gian cho một tiếng tíc theo người nào đó ngồi trên tàu kề bên đồng hồ đơn giản bằng 2/c, bởi vì đối với họ ánh sáng chỉ đơn giản truyền đi 2 mét với tốc độ c (quãng đường = tốc độ × thời gian nên thời gian = quãng đường / tốc độ). Lập tỉ số của hai khoảng thời gian này cho ta biết đồng hồ trên tàu chạy chậm bao nhiêu, khi đo bởi ai đó trên sân ga; nó chậm đi một hệ số c/√(c2 – v2) mà với một ít sắp xếp toán học, ta có thể viết lại là 1/√(1 – v2/c2). Đây là một đại lượng rất quan trọng trong thuyết tương đối, và nó thường được biểu diễn bởi kí tự Hi Lạp γ, phát âm là “gamma”. Lưu ý rằng γ luôn luôn lớn hơn 1 miễn là đồng hồ đang chuyển động chậm hơn tốc độ ánh sáng, bởi vì v/c sẽ nhỏ hơn 1. Khi v rất nhỏ so với tốc độ ánh sáng (tức là, đối với đa số tốc độ thông thường, vì theo đơn vị quen thuộc hơn của những người lái mô tô chuyên nghiệp thì tốc độ ánh sáng là 671 triệu dặm/giờ), γ thật sự rất gần với 1. Chỉ khi v trở nên lớn đáng kể so với tốc độ ánh sáng thì γ mới bắt đầu lệch nhiều với 1.
Bây giờ ta đã làm toán xong – ta đã thành công trong việc tính chính xác thời gian trôi chậm bao nhiêu trên đoàn tàu khi được xác định bởi ai đó trên sân ga. Bây giờ ta hãy thay số vào để có chút cảm giác về đáp số. Nếu đoàn tàu đang chuyển động 300 km/h, thì bạn có thể kiểm tra rằng v2/c2 là một con số rất nhỏ: 0,000000000000077. Để có hệ số “giãn nở thời gian”, ta cần 1/√0,000000000000077 = 1,000000000000039. Đúng như trông đợi, đó là một hiệu ứng rất nhỏ: Ngồi trên đoàn tàu chuyển động 100 năm sẽ chỉ kéo dài tuổi thọ của bạn thêm 0,000000000000039 năm, theo người bạn của bạn đứng trên sân ga, tức là hơn một phần mười của một mili giây một chút. Tuy nhiên, hiệu ứng sẽ không còn nhỏ như vậy nếu đoàn tàu lao vút đi với vận tốc bằng 90% tốc độ ánh sáng. Hệ số giãn nở thời gian khi đó sẽ lớn hơn 2, nghĩa là đồng hồ đang chuyển động sẽ gõ nhịp chậm hơn một nửa tốc độ của đồng hồ đứng yên theo người ngồi trên sân ga. Đây là tiên đoán của Einstein và, giống như mọi nhà khoa học nghiêm túc khác, ta phải kiểm tra nó trên thực nghiệm nếu ta tin vào nó. Tới đây thì nó trông có chút khó tin.
Phần tiếp theo >>