Chúng tôi trích giới thiệu với các bạn một số bản dịch từ tác phẩm Những câu hỏi và bài tập vật lí phổ thông của hai tác giả người Nga L. Tarasov và A. Tarasova, sách xuất bản ở Nga năm 1968. Bản dịch lại từ bản tiếng Anh xuất bản năm 1973.
Các bài giảng được trình bày dưới dạng thảo luận hỏi đáp giữa giáo viên và học sinh.
§21. Phương pháp giải bài toán các định luật chất khí
HS A: Em muốn khảo sát áp dụng của các định luật chất khí trong việc giải những bài toán khác nhau.
GV: Theo quan điểm của tôi, hầu như mọi bài toán liên quan đến các định luật chất khí yêu cầu thí sinh giải đều khá đơn giản. Đa số chúng thuộc một trong hai nhóm sau đây.
Nhóm thứ nhất: Những bài toán được nghĩ ra trên cơ sở một sự biến thiên trạng thái ở một khối lượng khí nhất định; giá trị của khối lượng không được dùng tới. Do sự giãn nở, nóng lên và những quá trình khác, chất khí chuyển từ một trạng thái nhất định với các thông số p1, V1 và T1 sang một trạng thái với các thông số p2, V2 và T2. Các thông số của trạng thái ban đầu và trạng thái sau cuối liên hệ với nhau theo phương trình của định luật chất khí kết hợp

Bài toán là đi tính một trong sáu thông số trạng thái này.
Nhóm thứ hai: Những bài toán trong đó trạng thái của chất khí không biến đổi nhưng giá trị của khối lượng chất khí có mặt trong bài toán. Nó yêu cầu hoặc tính khối lượng này khi tất cả các thông số là đã biết, hoặc tính một thông số khi khối lượng và những thông số kia là đã biết. Trong những bài toán như thế, trọng lượng phân tử của chất khí là phải biết trước.
HS B: Em nghĩ cách tiện nhất để giải những bài toán thuộc nhóm thứ hai là sử dụng phương trình (104) của định luật chất khí kết hợp.
GV: Tất nhiên em có thể sử dụng phương trình này. Tuy nhiên, để làm vậy, em phải biết giá trị số của hằng số chất khí R. Cứ như một quy tắc, chẳng ai nhớ giá trị đó cả. Vì lí do này, trên thực tế cách tiện hơn là sắp xếp lại theo phương pháp sau đây: chúng ta giả sử chất khí được mang đến điều kiện chuẩn, kí hiệu các thông số chất khí ở điều kiện này là pS, Vs và Ts. Khi đó ta có thể viết phương trình
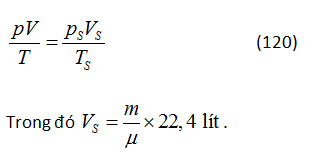
HS B: Theo em, phương pháp giải này chẳng có gì đơn giản hơn sử dụng phương trình (104). Ở đây chúng ta phải nhớ ba giá trị: pS = 76 cmHg, TS = 273 K và VS/(m/µ) = 22,4 lít. Rõ ràng nếu chỉ nhớ một giá trị số của hằng số chất khí thì dễ hơn.
GV: Tuy nhiên, phương pháp của tôi đơn giản hơn bởi vì chẳng ai có chút khó khăn gì trong việc ghi nhớ ba giá trị mà em nói (áp suất, nhiệt độ và thể tích của một phân tử gram chất khí dưới điều kiện chuẩn). Giả sử rằng chúng ta được yêu cầu tính thể tích của 58 g không khí ở áp suất 8 atm và nhiệt độ 91oC. Chúng ta hãy giải bài toán này bằng phương pháp mà tôi đề xuất. Vì khối lượng phân tử gram của không khí bằng 29 g nên chúng ta có 2 phân tử gram. Từ phương trình (120) ta thu được
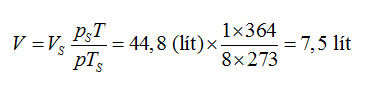
HS B: Em thấy thầy đã giả sử rằng pS = 1 atm. Tuy nhiên, dữ kiện của bài toán có khả năng cho theo đơn vị atmosphere kĩ thuật. Khi đó pS = 1,034 atm.
GV: Em nói đúng. Có một sự khác biệt giữa atmosphere vật lí (tương ứng với áp suất chuẩn) và atmosphere kĩ thuật. Để cho nhanh, tôi đã bỏ qua sự khác biệt này.
HS A: Thầy có thể trình bày cho chúng em biết những khó khăn tiêu biểu trong việc giải những bài toán thuộc nhóm thứ nhất và nhóm thứ hai hay không?
GV: Tôi đã nói theo quan điểm của tôi những bài toán này khá đơn giản.
HS A: Nhưng thường thì các thí sinh phạm phải những lỗi gì?
GV: Ngoài sự bất cẩn, nguyên nhân sai sót chủ yếu là không biết tính áp suất chất khí trong trường hợp này hay trường hợp khác. Xét một bài toán về một ống thủy tinh hàn kín ở một đầu. Cái ống chứa một cột thủy ngân tách li một thể tích khí nhất định với môi trường. Cái ống có thể quay trong một mặt phẳng thẳng đứng. Ở vị trí thứ nhất (Hình 80a), cột không khí trong ống có chiều dài l1 và ở vị trí thứ hai (Hình 80b), l2. Tìm chiều dài l3 của cột không khí ở vị trí thứ ba khi cái ống nghiêng một góc α so với phương thẳng đứng (Hình 80c). Chúng ta sẽ kí hiệu áp suất khí quyển là pA tính theo chiều dài của cột thủy ngân, và chiều dài của cột thủy ngân trong ống là Dl. Ở vị trí thứ nhất, áp suất của không khí trong ống rõ ràng bằng áp suất khí quyển. Ở vị trí thứ hai nó bằng hiệu (pA - Dl), vì áp suất khí quyển cân bằng với tổng áp suất của cột thủy ngân và không khí bên trong ống. Áp dụng định luật Boyle và Mariotte, ta viết
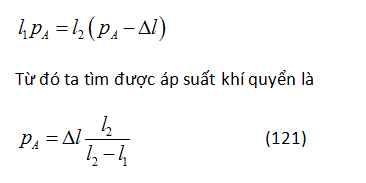
Ở vị trí thứ ba, một phần trọng lượng của cột thủy ngân sẽ cân bằng với phản lực của thành ống. Do đó, áp suất của không khí bên trong ống bằng (pA - Δl.cosα). Sử dụng định luật Boyle và Mariotte cho trạng thái thứ nhất và thứ ba của chất khí, ta có thể viết

Các em có thể dễ dàng thấy rằng nếu cosα = 1 thì l3 = l2, tức là ta có vị trí thứ hai của ống, và nếu cosα = 0 thì l3 = l1, tức tương ứng với vị trí thứ nhất của ống.
HS A: Nhóm bài toán thứ nhất và thứ hai theo phân loại của thầy thì em đã rõ. Nhưng liệu có khả năng thí sinh sẽ gặp những bài toán kết hợp của cả hai nhóm trên không thầy?
GV: Có chứ, không thể loại trừ một khả năng như thế. Ta hãy xét bài toán sau đây. Ở một áp suất 2 atm, 16 g oxygen chiếm một thể tích 5 lít. Hỏi nhiệt độ của chất khí biến thiên như thế nào nếu biết rằng áp suất tăng lên đến 5 atm và thể tích giảm đi 1 lít?
HS A: Khối lượng, áp suất và thể tích của khí oxygen là đã biết, ta có thể tìm nhiệt độ của nó ngay. 16 g oxygen là 0,5 phân tử gram, nó có thể tích 11,2 lít ở điều kiện chuẩn. Tiếp theo, ta tìm được

So sánh kết quả này với phương trình (124), ta thấy nhiệt độ đã tăng thêm 244 độ.
GV: Lời giải của em hoàn toàn đúng. Như các em có thể thấy, nửa phần sau của bài toán giải dưới dạng một dạng tiêu biểu thuộc nhóm thứ nhất.
HS B: Lúc chúng ta mới bắt đầu thảo luận, trong khi nói về những nhóm bài toán có thể gặp, thầy có nói là đa số các bài toán thuộc về những nhóm này. Liệu có những bài toán khác về nguyên lí với những bài thuộc nhóm thứ nhất và nhóm thứ hai không thưa thầy?
GV: À, có chứ. Trong những bài toán thuộc những nhóm này, người ta giả sử khối lượng của chất khí không thay đổi. Tuy nhiên, người ta có thể nghĩ ra những bài toán trong đó khối lượng của chất khí thay đổi (chất khí được bơm vào hoặc bơm ra khỏi bình chứa). Chúng sẽ phân loại tùy ý những bài toán như thế là thuộc nhóm thứ ba. Không có những quy tắc có sẵn nào để giải những bài toán như thế; chúng đòi hỏi một cách tiếp cận riêng trong từng trường hợp. Tuy nhiên, trong mỗi trường hợp riêng, các bài toán thuộc nhóm thứ ba có thể được suy giản thành những bài toán thuộc hai nhóm đầu hoặc sang dạng kết hợp của chúng. Ta có thể minh họa nội dung này bằng hai ví dụ sau đây.
Đây là ví dụ thứ nhất. Chất khí đựng trong một cái bình chịu áp suất 20 atm và nhiệt độ 27oC. Tính áp suất chất khí trong bình sau khi một nửa khối lượng khí đã được lấy ra khỏi bình và nhiệt độ của chất khí còn lại tăng thêm 50 độ.
Bài toán này tương tự với những bài thuộc nhóm thứ nhất, vì nó liên quan đến sự biến thiên trạng thái của một chất khí. Tuy nhiên, với sự biến thiên trạng thái thì khối lượng của chất khí cũng thay đổi. Để sử dụng định luật chất khí kết hợp, chúng ta phải xét sự biến thiên trạng thái của cùng một lượng khí. Chúng ta sẽ chọn khối lượng của chất khí cuối cùng còn lại trong bình. Ta kí hiệu các thông số sau cuối của nó là p2, V2 và T2. Khi đó T2 = (273 + 27 + 50) = 350 K, V2 = V, trong đó V là thể tích của bình chứa, và p2 là áp suất cần tính. Ta có thể biểu diễn các thông số ban đầu của lượng khí này như thế nào?
HS A: Nó sẽ có nhiệt độ của toàn bộ lượng khí T1 = (273 + 27) = 300 K; thể tích của nó sẽ bằng một nửa thể tích của bình, tức là V/2; và áp suất của nó bằng áp suất của toàn bộ lượng khí: p1 = 20 atm.
HS B: Em xử lí các thông số ban đầu của khối lượng khí đã nói ở trên hơi khác: T1 = 300 K, thể tích bằng thể tích của toàn bộ chất khí (V1 = V), nhưng áp suất bằng một một nửa áp suất của toàn bộ lượng khí, tức là p1 = 10 atm.
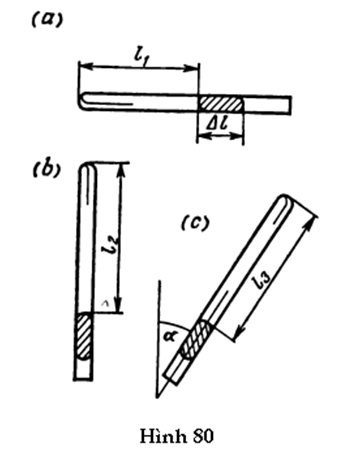
GV: Vì áp suất và thể tích có mặt trong phương trình ở dạng tích của chúng, cho nên mặc dù đề xuất của hai em có khác nhau nhưng chúng dẫn tới cùng một kết quả. Vì lí do này, chúng ta có thể tránh né những khác biệt này nếu chúng không đáng quan tâm từ quan điểm vật lí. Chúng ta sẽ tùy ý gọi những phân tử thuộc phần sau cùng còn ở lại trong bình là những phân tử “trắng”, còn những phân tử thuộc phần được lấy ra khỏi bình là những phân tử “đen”. Như vậy, chúng ta đồng ý rằng các phân tử trắng vẫn ở lại trong bình, và các phân tử đen được lấy ra khỏi bình. Trạng thái ban đầu của chất khí có thể được xét theo hai cách: (1) các phân tử đen và trắng tách riêng sao cho thể tích vĩ mô có thể tách riêng trong bình chỉ chứa phân tử trắng hoặc chỉ chứa phân tử đen (Hình 81a); (2) các phân tử đen và trắng trộn đều với nhau sao cho mỗi thể tích vĩ mô có chứa số phân tử thuộc mỗi loại là như nhau (Hình 81b). Trong trường hợp thứ nhất, các phân tử thuộc mỗi loại tạo ra “khối” khí riêng của chúng với thể tích V/2 tác dụng một áp suất 20 atm lên thành bình và lên ranh giới tưởng tượng với khối kia. Trong trường hợp thứ hai, các phân tử thuộc cả hai loại phân bố đều khắp thể tích V của bình, và các phân tử thuộc mỗi loại chỉ tác dụng một nửa áp suất lên thành bình (tại bất kì chỗ nào trên thành bình, một nửa áp suất là do các phân tử trắng tác dụng, một nửa còn lại là do các phân tử đen). Trong trường hợp này, V1 = V và p1 = 10 atm. Liên hệ với nhận xét vừa nói, chúng ta hãy nhắc lại định luật áp suất riêng phần: áp suất của một hỗn hợp khí bằng tổng áp suất của các chất khí thành phần. Tôi muốn nhấn mạnh ở đây là chúng ta đang xét một hỗn hợp khí, trong đó các phân tử thuộc cả hai loại ban đầu trộn lẫn với nhau.
HS B: Em nghĩ phương án thứ hai là chính xác hơn bởi vì các phân tử thuộc cả hai loại thật sự hòa lẫn với nhau.
GV: Trong bài toán đang xét, cả hai phương án đều có giá trị ngang nhau. Đừng quên rằng chuyện chúng ta phân chia thành các phân tử trắng và đen là hoàn toàn tùy tiện.
Nhưng ta hãy trở lại với việc giải bài toán. Chúng ta viết phương trình của định luật chất khí kết hợp cho khối khí vẫn còn lại trong bình
10V / 300 = p2V / 350
Từ đó ta tính được p2 = 11,7 atm.
Bây giờ xét bài toán sau. Một chất khí đựng trong một cái bình thể tích V ở áp suất p0. Nó được lấy ra khỏi bình bằng một bơm piston mỗi lần bơm được thể tích v (Hình 82). Tìm số lần bơm, n, cần thiết để hạ áp suất của chất khí trong bình xuống còn pn.

HS A: Bài toán này có vẻ khá đơn giản: số lượt bơm n của piston làm thể tích chất khí tăng thêm một lượng nv. Do đó, ta có thể viết định luật Boyle và Mariotte ở dạng
p0V = pn(V + nv)
từ đó ta tính được số lần bơm n.
GV: Khối lượng chất khí trong phương trình của em là chỉ cái gì?
HS A: Chỉ khối lượng ban đầu có trong bình.
GV: Nhưng ngay sau lần bơm thứ nhất, một phần của khối lượng này đã rời khỏi hệ hoàn toàn: khi piston chuyển động sang trái nó đóng van A và mở van B cho chất khí rời khỏi hệ (xem Hình 82). Độ tăng thể tích chất khí nv không chỉ cùng khối lượng khí đó. Như vậy, phương trình của em là không đúng.
Chúng ta hãy xét riêng từng lần bơm của piston. Ta sẽ bắt đầu với lần bơm thứ nhất. Đối với khối lượng khí ban đầu có trong bình ta có thể viết
p0V = p1 (V + v)
Trong đó p1 là áp suất của chất khí sau khi piston hoàn thành lần bơm thứ nhất và ở vị trí biên phía bên phải. Sau đó piston trở lại vị trí ban đầu phía bên trái của nó. Tại đây, như tôi đã nói ở phần trước, van A đóng và khối lượng khí trong bình nhỏ hơn khối lượng khí ban đầu. Áp suất của nó là p1. Đối với khối lượng khí này chúng ta có thể viết phương trình
p1V = p2 (V + v)
Trong đó p2 là áp suất của chất khí sau khi piston hoàn thành lần bơm thứ hai. Tiếp tục tương tự với lần bơm thứ ba, thứ tư, và những lần bơm tiếp sau đó của piston, ta thu được một hệ phương trình của định luật Boyle và Mariotte

Mỗi phương trình này ứng với một khối lượng khí nhất định. Giải hệ phương trình (125) ta được

Bài tập
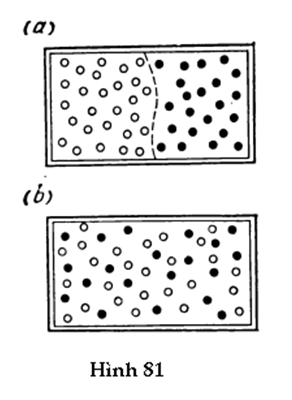
39. Một ống thủy tinh có một đầu hàn kín và được dìm hoàn toàn trong một bình chứa thủy ngân (Hình 83). Cột không khí bên trong ống có chiều cao 10 cm. Hỏi đầu trên của ống phải nâng lên đến độ cao nào so với mức thủy ngân trong bình để cho mức thủy ngân bên trong ống trùng với mức thủy ngân trong bình? Giả sử áp suất khí quyển chuẩn. Tính khối lượng của không khí bên trong ống nếu tiết diện của nó bằng 1 cm2. Cho biết nhiệt độ là 27oC.
40. Một ống thủy tinh, một đầu hàn kín, đầu hở được nhúng vào một bình chứa thủy ngân (Hình 84). Hỏi mức thủy ngân trong ống sẽ thay đổi như thế nào nếu nhiệt độ tăng từ 27oC lên 77oC? Bỏ qua sự giãn nở vì nhiệt của ống. Giả sử áp suất khí quyển chuẩn. Tính khối lượng không khí bên trong ống nếu tiết diện của nó là 0,5 cm2.
41. Không khí trong một cái bình thể tích 5 lít có nhiệt độ 27oC và chịu áp suất 20 atm. Khối lượng không khí phải lấy ra khỏi bình là bao nhiêu để cho áp suất của nó giảm còn 10 atm?
42. Tính công thực hiện bởi một chất khí đang được nung nóng đẳng áp từ 20oC lên 100oC nếu nó được đựng trong một cái bình đậy kín bởi một piston di động có tiết diện 20 cm2 và trọng lượng 5 kgf. Xét hai trường hợp: (1) cái bình đặt nằm ngang (Hình 85a); (2) cái bình đặt thẳng đứng (Hình 85b). Thể tích ban đầu của chất khí là 5 lít. Giả sử áp suất khí quyển chuẩn.
43. Một cột không khí dài 40 cm trong một ống thủy tinh có tiết diện 0,4 cm2 và được đặt thẳng đứng với đầu kín hướng lên trên, và được tách riêng bởi một cột thủy ngân dài 8 cm. Nhiệt độ là 27oC. Hỏi chiều dài của cột không khí sẽ biến thiên như thế nào nếu cái ống nghiêng 60o so với phương thẳng đứng đồng thời nhiệt độ tăng thêm 30 độ? Giả sử áp suất khí quyển chuẩn. Tính khối lượng của không khí bị nhốt kín trong ống.
44. Khối lượng của hơi nước trong một căn phòng kích cỡ 6 m x 5 m x 3,5 m bằng bao nhiêu nếu, ở nhiệt độ 15oC, độ ẩm tương đối là 55%. Sương có hình thành không nếu nhiệt độ giảm xuống còn 10oC? Khối lượng của hơi nước bằng bao nhiêu phần khối lượng không khí trong phòng nếu áp suất không khí bằng 75 cm Hg?
Những câu hỏi và bài tập vật lí phổ thông
L. Tarasov và A. Tarasova
Trần Nghiêm dịch
Phần tiếp theo >>

![Sách [Phiên chợ sách cũ] Siêu Tư Duy Vật Lý Luyện Đề THPT Quốc Gia 2016 2017](https://thuvienvatly.com/images/deals/thumb/sach-phien-cho-sach-cu-sieu-tu-duy-vat-ly-luyen-de-thpt-quoc-gia-2016-2017.jpg)