Chúng tôi trích giới thiệu với các bạn một số bản dịch từ tác phẩm Những câu hỏi và bài tập vật lí phổ thông của hai tác giả người Nga L. Tarasov và A. Tarasova, sách xuất bản ở Nga năm 1968. Bản dịch lại từ bản tiếng Anh xuất bản năm 1973.
Các bài giảng được trình bày dưới dạng thảo luận hỏi đáp giữa giáo viên và học sinh.
§7. Các bài toán động lực học khó giải hơn khi xét có ma sát
GV: Các bài toán có lẽ trở nên khó hơn nhiều khi xét đến lực ma sát.
HS: Nhưng chúng ta đã có nói về lực ma sát (§3). Nếu một vật đang chuyển động thì lực ma sát được xác định từ phản lực pháp tuyến (Ffr = kN); nếu vật đang đứng yên thì lực ma sát bằng lực có xu hướng làm vật rời khỏi trạng thái đứng yên này. Toàn bộ nội dung này chúng em đã hiểu và nhớ rồi.
GV: Đúng rồi. Tuy nhiên, em đã bỏ quên một thực tế quan trọng. Em giả sử em đã biết câu trả lời cho những câu hỏi sau đây: (1) Vật đang chuyển động hay nó đang đứng yên? (2) Vật đang chuyển động theo hướng nào? (nếu có chuyển động) Nếu những cái này đã được biết trước thì bài toán tương đối đơn giản. Nếu không, nó có thể rất phức tạp ngay từ lúc bắt đầu và có thể còn đòi hỏi sự khảo sát đặc biệt.
HS: Vâng, giờ thì em nhớ chúng ta có nói tới vấn đề này trong §2 liên quan đến phần thảo luận của chúng ta về việc chọn hướng của lực ma sát.
GV: Bây giờ tôi muốn thảo luận câu hỏi này chi tiết hơn. Theo quan điểm dứt khoát của tôi thì những khó khăn trong khi giải những bài toán có xét đến lực ma sát rõ ràng đã bị đánh giá thấp bởi học sinh và các tác giả nhất định khi soạn bài tập cho các sách giáo khoa vật lí.
Ta hãy xét ví dụ minh họa ở Hình 10. Góc nghiêng a của mặt phẳng nghiêng, trọng lượng P của vật, lực F và hệ số ma sát k là đã biết. Để cho đơn giản, ta sẽ giả sử rằng k0 = k (trong đó k0 là hệ số xác định lực ma sát nghỉ cực đại). Yêu cầu là xác định loại chuyển động của vật và tìm gia tốc.
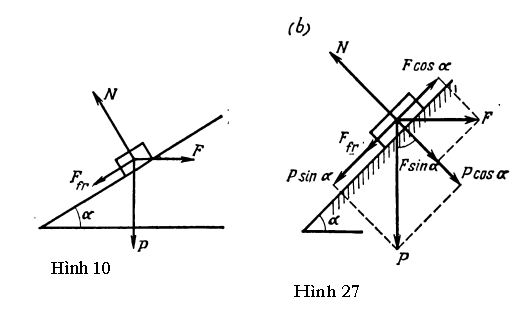
Ta hãy giả sử rằng vật trượt lên theo mặt phẳng nghiêng. Ta có thể phân tích các lực như trên Hình 27b và sử dụng kết quả thu được cho gia tốc trong §6. Như vậy
a = g/P [Fcosα – Psinα – (Pcosα + Fsinα)k] (24)
Theo phương trình (24) cho vật trượt lên mặt phẳng nghiêng, điều kiện sau đây phải được thỏa mãn
Fcosα – Psinα – (Pcosα + Fsinα)k >= 0
Điều kiện này có thể viết lại ở dạng
F >= P (kcosα + sinα)/(cosα – ksinα)
hay
F >= P (k + tanα )/(1 – ktanα) (25)
Chúng ta cũng sẽ giả sử rằng góc nghiêng của mặt phẳng nghiêng là không lớn lắm, sao cho (1 – ktanα) > 0, hay
tanα < 1/k (26)
Tiếp theo ta sẽ giả sử rằng vật trượt xuống mặt phẳng nghiêng. Một lần nữa ta phân tích tất cả các lực như ở Hình 27b nhưng đảo chiều lực ma sát. Kết quả là ta thu được biểu thức sau đây cho gia tốc của vật
a = g/P [Psinα – Fcosα – (Pcosα + Fsinα)k] (27)
Từ phương trình (27) suy ra để vật trượt xuống mặt phẳng nghiêng, điều kiện sau đây phải được thỏa mãn
Psinα – Fcosα – (Pcosα + Fsinα)k >= 0
Điều kiện này ta viết ở dạng
F <= P (sinα – kcosα)/(cosα + ksinα)
hay
F <= P (tanα – k)/(1 + ktanα) (28)
Trong trường hợp này ta sẽ giả sử góc nghiêng của mặt phẳng nghiêng là không nhỏ lắm, sao cho (tanα – k) > 0, hay
tanα > k (29)
Kết hợp các điều kiện (25), (26), (28) và (29), ta có thể đi tới những kết luận sau:
1. Giả sử điều kiện nghiệm đúng đối với một mặt phẳng nghiêng thì
(a) Nếu F > P (k + tanα)/(1 – k tanα) thì vật trượt lên trên với gia tốc có thể xác định theo phương trình (24);
(b) Nếu F = P (k + tanα)/(1 – k tanα) thì vật trượt lên với vận tốc không đổi hoặc nằm yên;
(c) Nếu F < P (tanα – k)/(1 + k tanα) thì vật trượt xuống với gia tốc có thể xác định theo phương trình (27);
(d) Nếu F = P (tanα – k)/(1 + k tanα) thì vật trượt xuống với vận tốc không đổi hoặc nằm yên;
(e) Nếu P (tanα – k)/(1 + k tanα) < F < P (k + tanα)/(1 – k tanα) thì vật nằm yên.
Lưu ý rằng khi tăng lực F từ P (tanα – k)/(1 + k tanα) đến P (k + tanα)/(1 – k tanα), lực ma sát nghỉ giảm dần từ k(Pcosα + Fsinα) về không; rồi sau khi hướng của nó đảo lại, nó tăng đến giá trị k(Pcosα + Fsinα). Trong khi điều này xảy ra, vật vẫn nằm yên.
2. Bây giờ giả sử mặt phẳng nghiêng thỏa mãn điều kiện
0 < tanα <= k
thì
(a) Nếu F > P (k + tanα)/(1 – k tanα) thì vật trượt lên với gia tốc có thể xác định theo phương trình (24);
(b) Nếu F = P (k + tanα)/(1 – k tanα) thì vật trượt lên với vận tốc không đổi hoặc nằm yên;
(c) Nếu F < P (k + tanα)/(1 – k tanα) thì vật nằm yên; mọi chuyển động hướng xuống của vật trên mặt phẳng nghiêng là không thể (cho dù lực F có triệt tiêu).
3. Cuối cùng, ta hãy giả sử mặt phẳng nghiêng thỏa mãn điều kiện
tanα >= 1/k
thì
(a) Nếu F < P (tanα – k)/(1 + k tanα) thì vật trượt xuống với gia tốc có thể xác định theo phương trình (27);
(b) Nếu F = P (tanα – k)/(1 + k tanα) thì vật trượt xuống với vận tốc không đổi hoặc nằm yên;
(c) Nếu F > P (tanα – k)/(1 + k tanα) thì vật nằm yên; mọi chuyển động hướng lên của vật trên mặt phẳng nghiêng là không thể. Thoạt nhìn, kết luận này trông như không hoàn chỉnh vì lực F có thể tăng lên đến vô hạn! Tuy nhiên, vì góc nghiêng của mặt phẳng nghiêng khá lớn, nên với sự tăng lực F thì áp lực của vật nặng tác dụng lên mặt phẳng nghiêng sẽ tăng với tốc độ còn nhanh hơn.
HS: Chưa có loại nào như vậy được chứng minh với chúng em ở trường học cả.
GV: Đây chính là lí do tôi muốn hướng sự chú ý của các em tới vấn đề này. Tất nhiên, trong bài thi đầu vào của các em, rõ ràng các em sẽ phải giải những trường hợp đơn giản hơn nhiều: sẽ không có lực ma sát, hoặc sẽ có lực ma sát nhưng bản chất của chuyển động sẽ được biết trước (chẳng hạn, cho biết vật đang chuyển động hay nằm yên). Tuy nhiên, cho dù ta không phải bơi trong những bể bơi sâu, nhưng tốt hơn ta nên biết chỗ sâu đó nằm ở đâu.
HS: Điều gì sẽ xảy ra nếu như ta giả sử k = 0?
GV: Khi không có ma sát, mọi thứ trở nên đơn giản hơn ngay. Với mọi góc nghiêng của mặt phẳng nghiêng, kết quả sẽ là:
Khi F > Ptanα, vật trượt lên với gia tốc
a = g/P (Fcosα – Psinα) (30)
Khi F = Ptanα, vật trượt với vận tốc không đổi (hướng lên hoặc hướng xuống), hoặc nằm yên;
Khi F < Ptanα, vật trượt xuống với gia tốc
a = g/P (Psinα – Fcosα) (31)
Lưu ý rằng kết quả của các phương trình (30) và (31) chỉ khác nhau dấu cộng trừ. Do đó, khi giải bài tập, em có thể giả sử một cách an toàn chiều chuyển động bất kì, tìm a và chú ý dấu của gia tốc. Nếu a > 0 thì vật chuyển động theo hướng mà em đã giả sử; nếu a < 0 thì vật sẽ chuyển động theo chiều ngược lại (gia tốc sẽ bằng |a|).
Ta hãy xét thêm một bài tập nữa. Hai vật P1 và P2 nối với nhau bằng một sợi dây vắt qua một cái ròng rọc. Vật P1 nằm trên một mặt phẳng nghiêng có góc nghiêng a và hệ số ma sát k; vật P2 treo dưới sợi dây (Hình 32). Tìm gia tốc của hệ.
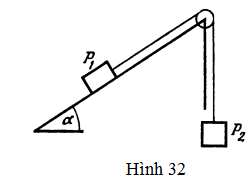
Giả sử hệ đang chuyển động từ trái sang phải. Xét chuyển động của hệ như một tổng thể, ta có thể viết phương trình sau đây cho gia tốc
a = g(P2 – P1sinα – P1kcosα)/(P1 + P2) (32)
Bây giờ giả sử hệ chuyển động từ phải sang trái, ta thu được
a = g(P1sinα – P2 –P1kcosα)/(P1 + P2) (33)
Ta sẽ tiến hành khảo sát cho các giá trị α và k đã biết, cho tỉ số p = P2/P1 biến thiên. Từ phương trình (32), ta suy ra đối với chuyển động từ trái sang phải thì điều kiện
p <= 1/(sinα + kcosα)
phải được thỏa mãn. Phương trình (33) gợi ý rằng đối với chuyển động từ phải sang trái thì điều kiện cần là
p >= 1/(sinα – kcosα)
Ở đây cần thêm một điều kiện nữa: góc nghiêng không nên quá nhỏ, tức là tanα > k. Nếu tanα <= k thì hệ sẽ không chuyển động từ phải sang trái, tuy rằng tỉ số p có thể lớn.
Nếu tanα > k thì vật nằm yên mang lại bất đẳng thức sau đây là đúng
1/(sinα + kcosα) < p < 1/(sinα – kcosα)
Nếu, thay vậy, tanα <= k thì vật nằm yên với
p > 1/(sinα + kcosα)
HS: Và điều gì sẽ xảy ra nếu ta thay đổi góc a hay hệ số k?
GV: Tôi để vấn đề này lại làm bài tập về nhà cho các em (xem bài tập 13 và 14).
Bài tập
13. Khảo sát bài toán minh họa trong Hình 32, giả sử rằng góc a của mặt phẳng nghiêng và tỉ số p = P2/P1 là đã biết, và gán những giá trị khác nhau cho hệ số k.
14. Khảo sát bài toán minh họa trong Hình 32, giả sử hệ số ma sát k và tỉ số p = P2/P1 là đã biết, và gán những giá trị khác nhau cho góc a của mặt phẳng nghiêng. Để cho đơn giản, hãy chỉ sử dụng hai giá trị: p = 1 (hai trọng lượng bằng nhau) và p = ½ (vật ở trên mặt phẳng nghiêng nặng gấp đôi vật treo dưới sợi dây).
Những câu hỏi và bài tập vật lí phổ thông
L. Tarasov và A. Tarasova
Trần Nghiêm dịch
Phần tiếp theo >>
