Chúng tôi trích giới thiệu với các bạn một số bản dịch từ tác phẩm Những câu hỏi và bài tập vật lí phổ thông của hai tác giả người Nga L. Tarasov và A. Tarasova, sách xuất bản ở Nga năm 1968. Bản dịch lại từ bản tiếng Anh xuất bản năm 1973.
Các bài giảng được trình bày dưới dạng thảo luận hỏi đáp giữa giáo viên và học sinh.
§11. Giải bài toán dao động điều hòa
GV: Một số thí sinh không hiểu rõ cho lắm các dao động điều hòa. Trước tiên ta hãy nói về định nghĩa của chúng.
HS A: Các dao động được gọi là điều hòa nếu chúng tuân theo định luật sin: li độ x của một vật tính từ vị trí cân bằng của nó biến thiên theo thời gian theo hàm
x = A sin(ωt + α) (65)
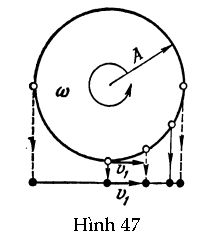
trong đó A là biên độ dao động (li độ cực đại của vật tính từ vị trí cân bằng), ω là tần số góc (ω = 2π/T, trong đó T là chu kì của dao động), và α là pha ban đầu (nó cho biết li độ của vật tính từ vị trí cân bằng tại thời điểm t = 0). Có thể xem dao động điều hòa là chuyển động của hình chiếu của một điểm quay với vận tốc góc không đổi ω trong một vòng tròn bán kính A (Hình 47).
HS B: Em thích một định nghĩa khác của dao động điều hòa. Như ta biết, các dao động xảy ra là do tác dụng của lực hồi phục, tức là một lực hướng về vị trí cân bằng và tăng lên khi vật tiến ra xa vị trí cân bằng. Dao động điều hòa là những dao động trong đó lực hồi phục F tỉ lệ với li độ x của vật tính từ vị trí cân bằng. Tức là
F = kx (66)
Một lực như vậy được gọi là “có tính đàn hồi”.
GV: Tôi hoàn toàn hài lòng với cả hai định nghĩa vừa nêu. Trong trường hợp thứ nhất, dao động điều hòa được định nghĩa theo cách chúng xảy ra; trong trường hợp thứ hai là theo nguyên nhân của chúng. Nói cách khác, định nghĩa thứ nhất sử dụng mô tả không gian-thời gian (động học) của dao động, còn định nghĩa thứ hai sử dụng mô tả nguyên nhân (động lực học).
HS B: Nhưng trong hai định nghĩa, cái nào được ưa thích hơn? Hoặc, có lẽ, chúng là tương đương nhau?
GV: Không, chúng không tương đương nhau, và định nghĩa thứ nhất (động học) được ưa chuộng hơn. Nó hoàn chỉnh hơn.
HS B: Nhưng cho dù bản chất của lực hồi phục là gì, rõ ràng nó sẽ xác định bản chất của dao động. Như vậy, em không hiểu tại sao định nghĩa của em lại kém hoàn chỉnh hơn.
GV: Câu này em nói không đúng lắm. Bản chất của lực hồi phục không hoàn toàn xác định bản chất của dao động.
HS A: Rõ ràng bây giờ là lúc nên nhắc lại rằng bản chất của chuyển động của một vật tại một thời điểm cho trước được xác định không chỉ bởi những lực tác dụng lên vật tại thời điểm đã cho, mà còn bởi các điều kiện ban đầu nữa, tức là vị trí và vận tốc của vật tại thời điểm ban đầu. Chúng ta đã nói vấn đề này ở §4.
GV: Rất đúng. Đối chiếu với trường hợp đang xét thì phát biểu này có nghĩa là bản chất của các dao động được xác định không chỉ bởi lực hồi phục, mà còn bởi những điều kiện mà những dao động này được bắt đầu. Rõ ràng các dao động có thể bị ảnh hưởng bởi những cách khác nhau. Chẳng hạn, một vật có thể bị kéo lệch một khoảng nhất định khỏi vị trí cân bằng và sau đó thả ra nhẹ nhàng. Nó sẽ bắt đầu dao động. Nếu dao động bắt đầu tại thời điểm zero thì phương trình (65) ta thu được α = π/2, và khoảng lệch của vật là biên độ dao động. Vật có thể bị kéo lệch những khoảng khác nhau tính từ vị trí cân bằng, do đó mang lại những biên độ dao động khác nhau.
Một phương pháp khác kích hoạt dao động là truyền một vận tốc ban đầu nhất định (bằng cách đẩy) cho một vật ở trường hợp cân bằng. Vật sẽ bắt đầu dao động. Chọn lúc bắt đầu dao động là thời điểm zero, ta thu được từ phương trình (65) α = 0. Rõ ràng còn có thể đề xuất vô số phương pháp trung gian khác để kích thích dao động. Chẳng hạn, một vật bị kéo lệch khỏi vị trí cân bằng của nó, và đồng thời bị đẩy hoặc bị kéo... Mỗi phương pháp này sẽ mang lại một giá trị rõ ràng của biên độ A và pha ban đầu α của dao động.
HS B: Ý thầy nói là các đại lượng A và α không phụ thuộc vào bản chất của lực hồi phục phải không?
GV: Đúng vậy. Em xử lí hai đại lượng này tùy ý khi em kích thích dao động bằng phương pháp này hoặc phương pháp kia. Lực hồi phục, tức là hệ số k trong phương trình (66), chỉ xác định tần số góc ω hay, nói cách khác, chu kì dao động của vật. Có thể nói rằng chu kì dao động là một đặc trưng riêng của hệ dao động, còn biên độ A và pha ban đầu α tùy thuộc vào các điều kiện bên ngoài kích thích dao động đã cho.
Trở lại với định nghĩa dao động điều hòa, chúng ta thấy rằng định nghĩa động lực học không chứa thông tin gì hoặc về biên độ hoặc về pha ban đầu. Trái lại, định nghĩa động học có chứa thông tin về những đại lượng này.
HS B: Nhưng nếu chúng ta có quyền tự do xử lí biên độ, thì có lẽ nó không phải là một đặc trưng quan trọng của một vật dao động?
GV: Em sai rồi. Biên độ là một đặc trưng rất quan trọng của một vật dao động. Để chứng minh điều này, ta hãy xét một ví dụ. Một quả cầu khối lượng m được gắn với hai lò xo đàn hồi và thực hiện dao động điều hòa với biên độ A theo phương ngang (Hình 48). Lực hồi phục được xác định bởi hệ số đàn hồi k đặc trưng cho tính đàn hồi của hai lò xo. Hãy tìm năng lượng của quả cầu đang dao động.
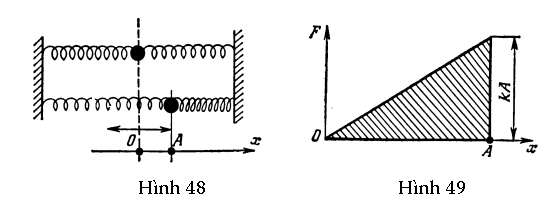
HS A: Để tìm năng lượng của quả cầu, ta có thể xét vị trí của nó lúc bị lệch nhiều nhất (x = A). Ở vị trí này, vận tốc của quả cầu bằng không và do đó năng lượng toàn phần của nó là thế năng của nó. Thế năng đó có thể xem là công thực hiện chống lại lực đàn hồi làm dịch chuyển quả cầu một khoảng A tính từ vị trí cân bằng của nó. Như vậy
W = FA (67)
Sau đó, tính đến F = kA, theo phương trình (66), ta thu được
W = kA2
GV: Em suy luận theo hướng đúng, nhưng đã phạm một sai sót. Phương trình (67) chỉ có thể áp dụng trong điều kiện lực không đổi. Trong trường hợp đã cho, lực F biến thiên theo li độ, như thể hiện trên Hình 49. Công thực hiện bởi lực này trên quãng đường x = A bằng diện tích gạch chéo nằm dưới đường cong lực. Đây là diện tích của một tam giác và bằng kA2/2. Như vậy
W = kA2/2 (68)
Lưu ý rằng năng lượng toàn phần của một vật dao động tỉ lệ với bình phương của biên độ dao động. Điều này chứng minh biên độ là một đặc trưng quan trọng như thế nào của một vật dao động.
Nếu 0 < x < A thì năng lượng toàn phần W bằng tổng hai thành phần – động năng và thế năng
W = kA2/2 = mv2/2 + kx2/2 (69)
Phương trình (69) cho phép tính vận tốc v của một vật dao động tại li độ x bất kì tính từ vị trí cân bằng. Câu hỏi tiếp theo của tôi là: chu kì dao động của quả cầu ở Hình 48 là bao nhiêu?
HS B: Để tìm công thức chu kì dao động sẽ cần sử dụng giải tích.
GV: Nói đại khái thì em đúng. Tuy nhiên, nếu chúng ta đồng thời sử dụng định nghĩa động học và động lực học của dao động điều hòa, ta có thể không cần sử dụng giải tích. Trước tiên, ta có thể kết luận từ Hình 47, đó là một biểu diễn hình học của định nghĩa động học, rằng vận tốc của vật tại thời điểm khi nó đi qua vị trí cân bằng là
v1 = ωA = 2πA/T (70)
Sử dụng kết quả của phương trình (68), theo định nghĩa động lực học, ta có thể kết luận rằng vận tốc v1 có thể tìm được từ hệ thức năng lượng
mv12/2 = kA2/2 (71)
(tại thời điểm quả cầu đi qua vị trí cân bằng, toàn bộ năng lượng của quả cầu là động năng). Kết hợp phương trình (70) và (71), ta thu được 4π2A2m/T2 = kA2, suy ra
T = 2π√(m/k) (72)
Như đã nói ở phần trước, chu kì dao động được xác định hoàn toàn bởi tính chất của bản thân hệ dao động, và độc lập với cách kích thích dao động.
HS A: Khi nói tới các dao động, ta thường xử lí không phải một quả cầu gắn với lò xo, mà là một con lắc. Những kết quả vừa thu được có thể khái quát hóa để bao hàm cả con lắc hay không?
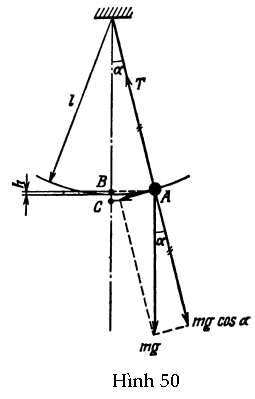
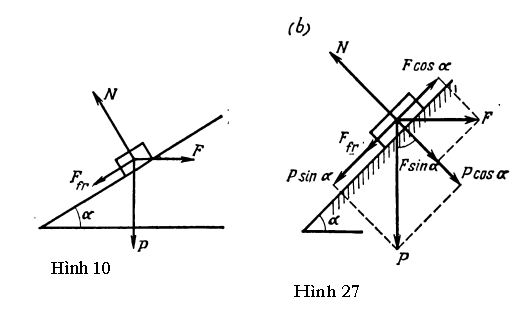
GV: Để khái quát hóa như vậy, trước tiên ta phải làm rõ xem, trong trường hợp con lắc, cái gì giữ vai trò của hệ số đàn hồi k. Rõ ràng con lắc dao động không phải do lực đàn hồi, mà là do trọng lực. Ta hãy xét một quả cẩu (trong con lắc gọi là quả lắc) treo dưới một sợi dây chiều dài l. Ta kéo quả cầu về một phía của vị trí cân bằng sao cho sợi dây hợp một góc α (Hình 50) với phương thẳng đứng. Có hai lực tác dụng lên quả lắc: trọng lực mg và lực căng T của sợi dây. Hợp lực của chúng là lực hồi phục. Từ hình vẽ ta thấy nó bằng mg sina.
HS A: Chiều dài nào, AB hay AC, được xem là độ lệch của con lắc khỏi vị trí cân bằng (xem Hình 50)?
GV: Chúng ta đang phân tích dao động điều hòa của một con lắc. Như vậy, cái cần thiết là góc lệch tối đa của sợi dây khỏi vị trí cân bằng phải rất nhỏ
α << 1 (73)
(lưu ý rằng góc a ở đây được tính theo radian; tính theo độ, thì góc α, trong mọi trường hợp, phải nhỏ hơn 10o). Nếu điều kiện (73) được thỏa mãn, thì sự chênh lệch giữa chiều dài AB và AC là có thể bỏ qua.
AB = l sinα ≈ AC = l tanα
Vì thế, câu hỏi của em trở nên không đáng để tâm. Để cho rõ ràng, ta có thể giả sử rằng x = AB = l sinα. Khi đó phương trình (66) sẽ có dạng sau đây cho một con lắc
mg sinα = kl sinα (66a)
từ đó
k = mg/l (74)
Thay phương trình này vào phương trình (72), ta thu được công thức cho chu kì dao động của một con lắc
T = 2π√(l/g) (75)
Chúng ta cũng trả lời cho câu hỏi năng lượng của con lắc. Năng lượng toàn phần của nó rõ ràng bằng mgh, trong đó h là độ cao quả lắc nâng lên ở vị trí lệch nhiều nhất (xem Hình 50). Như vậy
W = mgh = mgl(1 - cosα) = 2mgl sin2 α/2 (76)
Công thức (76) rõ ràng thích hợp cho mọi giá trị của góc a. Để chuyển kết quả này thành hệ thức (68), cần thỏa mõa điều kiện điều hòa của dao động của con lắc, tức là bất đẳng thức (73). Khi đó sina có thể lấy gần đúng bằng góc a tính theo radian, và phương trình (76) sẽ chuyển thành
nghĩa là, về thực chất, giống như phương trình (68).
HS B: Nếu em nhớ chính xác thì trong phần khảo sát trước đây về dao động của con lắc, ta không cần điều kiện góc lệch nhỏ.
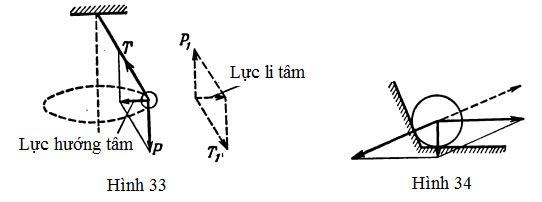
GV: Yêu cầu này là không cần thiết nếu chúng ta chỉ xét năng lượng của quả lắc hay lực căng của sợi dây. Trong trường hợp đã cho, thật ra chúng ta đang xét không phải con lắc, mà là chuyển động của một quả cầu trong một vòng tròn trong mặt phẳng thẳng đứng. Tuy nhiên, nếu bài toán cần dùng công thức (75) cho chu kì dao động, thì dao động của con lắc đòi hỏi phải điều hòa và do đó góc lệch phải là nhỏ. Ví dụ, trong bài tập 33, điều kiện góc lệch nhỏ của con lắc là không cần thiết, còn trong bài tập 34 điều kiện đó có tầm quan trọng thiết yếu.
Bài tập
32. Một quả cầu thực hiện một dao động điều hòa như biểu diễn ở Hình 48. Tìm tỉ số vận tốc của quả cầu tại điểm có li độ bằng một nửa và một phần ba biên độ.
33. Một quả lắc treo dưới một sợi dây bị lệch khỏi vị trí cân bằng một góc 60o và sau đó được thả ra. Tìm tỉ số lực căng của sợi dây tại vị trí cân bằng và tại vị trí góc lệch lớn nhất.
34. Một con lắc ở dạng một quả cầu (quả lắc) treo dưới một sợi dây bị kéo lệch một góc 5o. Tìm vận tốc của quả lắc tại thời điểm nó đi qua vị trí cân bằng nếu tần số góc của dao động của con lắc là 2 s-1.
Trần Nghiêm dịch
![[Mã BMLT35 giảm đến 35K] Sách Combo Vật Lý Đại Cương Tập 2 + Bài Tập Vật Lí Đại Cương Tập 2: (Điện - Dao Động - Sóng)](https://thuvienvatly.com/images/deals/thumb/ma-bmlt35-giam-den-35k-sach-combo-vat-ly-dai-cuong-tap-2-bai-tap-vat-li-dai-cuong-tap-2-dien-dao-dong-song.jpg)
