Thuvienvatly.com giới thiệu bản dịch tập sách Vật lí - Các khái niệm và quan hệ, một bộ sách giáo khoa vật lí trình bày sinh động, dễ hiểu. Bộ sách gồm nhiều tác giả biên soạn. Chúng tôi sẽ đăng nhiều kì bản dịch này. Mời các bạn đón xem.


Với ba định luật đơn giản, Newton đã giải thích mọi chuyển động xung quanh chúng ta. Nhưng, những định luật này mất đến hàng nghìn năm trời để thiết lập. Mặc dù người Hi Lạp cổ đại đã có nhiều đóng góp có giá trị cho toán học, triết học, văn học, và các khoa học, nhưng họ không làm thí nghiệm để kiểm tra toàn bộ những quan điểm khoa học của họ, cho nên dẫn tới một số kết luận sai lầm.
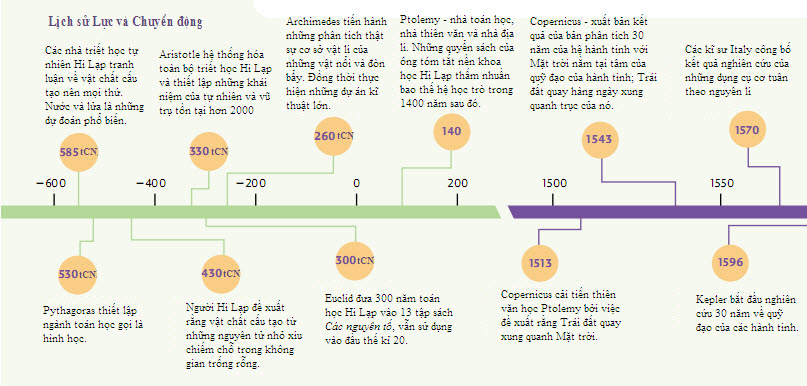
Phương pháp khoa học chính thức được phát triển và áp dụng trong Thời đại Ánh sáng (thế kỉ 17 và 18). Hệ quả là nhiều tiến bộ quan trọng đã được thực hiện trong nhiều lĩnh vực khoa học. Nicolas Copernicus (1473–1543), một nhà toán học người Ba Lan, đã giải thích chuyển động hàng ngày của Mặt trời và các ngôi sao với việc đề xuất rằng Trái đất quay quanh trục của nó. Galileo Galilei (1564–1642), một nhà toán học người Italy, đã làm thí nghiệm rộng rãi để kiểm tra những lí thuyết cổ đại của sự chuyển động. Thí nghiệm nổi tiếng của ông thả rơi hai hòn đá, một lớn và một nhỏ, từ Tháp nghiêng Pisa đã bác bỏ quan niệm cổ đại cho rằng khối lượng quyết định tính chất của chuyển động. Sự tìm hiểu cơ học thiên thể đã phát triển nhanh chóng với Johannes Kepler (1571–1630), người giải thích chuyển động thiên thể bằng cách sử dụng dữ liệu của Tycho Brahe (1546–1601). Ngài Isaac Newton (1642–1727) đã phát triển khái niệm lực hấp dẫn và thiết lập cơ sở của những quan niệm hiện nay của chúng ta về sự chuyển động trong tập sách đã xuất bản của ông tựa đề là Principia Mathematica. Với ba định luật của ông và sự phát triển những phương pháp toán học ngày nay gọi là giải tích, Newton đã xây dựng nên kiến thức của chúng ta về động học và động lực học. Newton và Galileo đã sáng tạo ra một phương pháp mới cho phân tích khoa học – kiểm tra và làm thí nghiệm – phương pháp chúng ta vẫn sử dụng ngày nay.
Trong phần này, chúng ta sẽ học những phương pháp khác nhau dùng để nghiên cứu các loại lực đa dạng từ sự chuyển động đơn giản, đến chuyển động có ma sát, và chuyển động quỹ đạo. Chúng ta cũng sẽ giải thích sự vận động của con người, và nguyên nhân ẩn sau thiết kế của những loại thiết bị khác nhau, như ván trượt tuyết và lốp ô tô, theo những định luật cổ điển của vật lí học. Phần này xây dựng nền tảng cho những phần sau nói về động lượng, năng lượng, trường, và vật lí hiện đại.



1.1 Giới thiệu
Mỗi ngày, chúng ta thấy hàng trăm vật đang chuyển động. Xe hơi chạy trên đường, bạn dẫn chó đi dạo trong công viên, lá rơi xuống đất. Những sự kiện này là bộ phận cấu thành nên kinh nghiệm hàng ngày của chúng ta. Vì thế, chẳng có gì bất ngờ khi mà một trong những chủ đề đầu tiên mà các nhà vật lí tìm cách tìm hiểu lại là sự chuyển động.
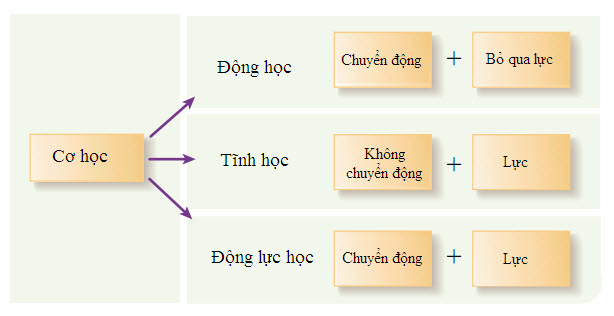
Nghiên cứu sự chuyển động được gọi là cơ học. Nó được chia thành hai phần, động học và động lực học. Động học là “cách thức” chuyển động, nghĩa là nghiên cứu các vật chuyển động như thế nào mà không bàn tới nguyên do vì sao chúng chuyển động như vậy. Động lực học là “vì sao” chuyển động. Trong động lực học, chúng ta quan tâm tới các nguyên nhân của sự chuyển động, đó là nghiên cứu lực. Trong hai chương tiếp theo, chúng ta sẽ xét các khía cạnh của động học và động lực học trong mối liên hệ với sự chuyển động xung quanh chúng ta.

1.2 Quãng đường và Độ dời
Trong bất kì lĩnh vực nào, việc sử dụng ngôn ngữ chính xác là quan trọng để người này có thể hiểu công việc của người khác. Mỗi lĩnh vực có những khái niệm nhất định được xem là những viên gạch cấu trúc cơ bản của ngành học đó. Khi bắt đầu tìm hiểu vật lí học, nhiệm vụ đầu tiên của chúng ta là định nghĩa một số khái niệm cơ bản mà chúng ta sẽ sử dụng trong suốt tập sách này.
Giả sử một người bạn ở dưới quê hỏi bạn, “Làm thế nào anh đi từ đây tới Vịnh Bắc?” Bạn trả lời, “Vịnh Bắc ở cách đây 400km”. Câu trả lời như thế này là đủ hay chưa? Chưa, vì bạn chỉ mới nói với bạn mình quãng đường đi tới Vịnh Bắc, bạn chưa cho cô ấy biết nên đi hướng nào. Câu trả lời của bạn là một vô hướng. Một vô hướng là một đại lượng chỉ có độ lớn, trong trường hợp này là 400 km. Một câu đáp như “Vịnh Bắc cách đây 400 km về hướng đông” sẽ trả lời câu hỏi trên rõ ràng hơn nhiều. Câu trả lời này là một câu trả lời vector. Một vector là một đại lượng có cả độ lớn và hướng. “400 km về hướng đông” là một thí dụ của một vector độ dời, trong đó độ lớn của độ dời là 400 km và hướng là hướng đông. Độ dời là sự thay đổi vị trí của một vật. Đơn vị chuẩn SI hay đơn vị hệ mét là mét (m), và kí hiệu của độ dời là . Những thí dụ của vô hướng là: 10 phút, 30oC, 4,0 lít, 10 m. Những thí dụ của vector là: 100 km [đông], 2,0 m [lên], 3,5 m [xuống]. Độ dời thường bị nhầm với quãng đường. Quãng đường là chiều dài đường đi và không có hướng, vì thế nó là một vô hướng.
Vị trí là một đại lượng vector cho biết vị trí của một vật so với người quan sát.
Ví dụ 1. Quãng đường và độ dời
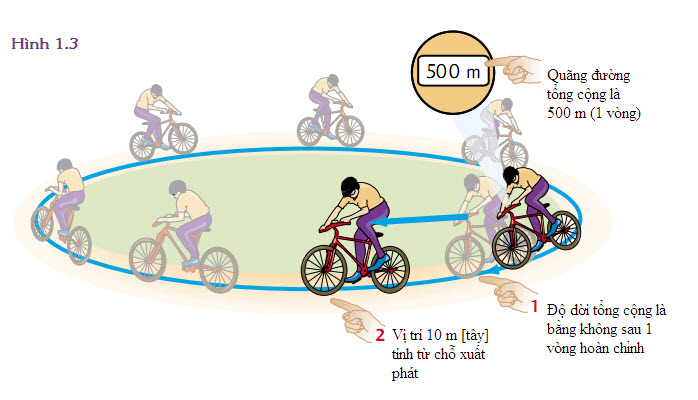
Một người đi xe đạp chạy 10 vòng quanh một vòng tròn 500 m (Hình 1.3). Quãng đường đã đi là bao nhiêu, và độ dời cuối cùng của người đi xe đạp đó là bao nhiêu?
Bài giải và liên hệ lí thuyết
Mỗi lần chạy đủ một vòng, người đi xe đạp đã đi được một quãng đường 500 m. Vì cô ta chạy 10 vòng, nên quãng đường tổng cộng là 5000 m. Để tìm độ dời của người đi xe đạp, chúng ta vẽ một đoạn thẳng từ điểm xuất phát đến điểm cuối của chuyển động. Vì cô ta bắt đầu và kết thúc tại cùng một điểm, nên độ dời của cô ta có độ lớn bằng không.
Trong thí dụ này, chúng ta thu được câu trả lời rất khác nhau cho quãng đường và độ dời. Nó là một thí dụ cho thấy rõ tầm quan trọng của việc phân biệt giữa đại lượng vector và đại lượng vô hướng.
Định nghĩa chiều
Trong những bài toán vector hai chiều, các chiều thường được cho theo bốn hướng chính: bắc, nam, đông, và tây. Với những bài toán một chiều hay tuyến tính, chúng ta sử dụng các chiều của hệ tọa độ Descartes chuẩn: những vector hướng sang phải và hướng lên trên là dương, và những vector hướng sang trái hoặc xuống dưới là âm.
1.3 Phân tích và Đổi đơn vị
Ngày xưa, khi hệ thống đo lường Anh được sử dụng phổ biến, thường xuyên xuất hiện nhu cầu chuyển đổi từ một hệ đơn vị này sang một hệ đơn vị khác. Ngày nay, với việc sử dụng hệ SI hay hệ mét, sự chuyển đổi giữa các đơn vị thỉnh thoảng mới phải làm. Để đổi tốc độ của một chiếc xe hơi đang chạy 100 km/h sang m/s, chúng ta nhân giá trị ban đầu với một dãy tỉ số, mỗi tỉ số bằng một. Chúng ta lập những tỉ số này theo những đơn vị mà chúng ta không muốn triệt tiêu, để lại những đơn vị của đáp số đúng. Thí dụ,

3,6 là một thừa số chuyển đổi cần nhớ. Để đổi m/s sang km/h, ta nhân với 3,6. Để đổi km/h sang m/s, ta chia cho 3,6.

Ví dụ 2. Đổi đơn vị
Có bao nhiêu giây trong 18 năm?
Bài giải và liên hệ lí thuyết
Giả sử một năm có 365 ngày.
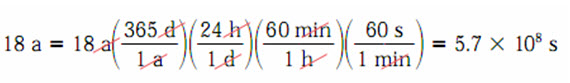
Có 5,7 x 108 s trong 18 năm.
Phân tích khái niệm
- Có bao nhiêu giây trong một tháng gồm 30 ngày?
- Một đường đua ngựa dài 7 furlong. Hỏi những con ngựa đua phải chạy bao nhiêu km? (Gợi ý: 8 furlong = 1 dặm, 1 km = 0,63 dặm)
- Sữa thường được bán theo quart. Một quart Anh gồm 20 ounce chất lỏng (1 oz = 27,5 ml). Hỏi có bao nhiêu ml sữa trong một quart?
Vật lí - Các khái niệm và quan hệ























![[ebook] Lỗ đen, lỗ sâu và cỗ máy thời gian](/bai-viet/images/2020/06/loden2.png)