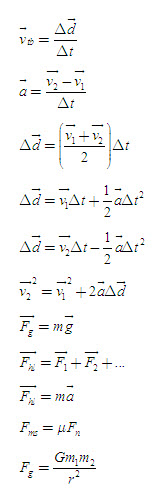1.8 Phân tích đồ thị của chuyển động thẳng
Cho đến đây, những ví dụ ta đã nghiên cứu là những bài toán đại số. Vì thế, ta đã sử dụng những lời giải đại số. Thông thường trong vật lí học, đặc biệt khi tiến hành các thí nghiệm, số liệu được biểu diễn ở dạng đồ thị. Vì vậy, các nhà vật lí cần biết phân tích số liệu trên đồ thị.
Có ba loại đồ thị chính được dùng trong động học: đồ thị vị trí – thời gian, đồ thị vận tốc – thời gian, và đồ thị gia tốc – thời gian. Mối quan hệ giữa những đồ thị này mang lại cho chúng ta một số công cụ phân tích mạnh nhất của mình.
Vận tốc
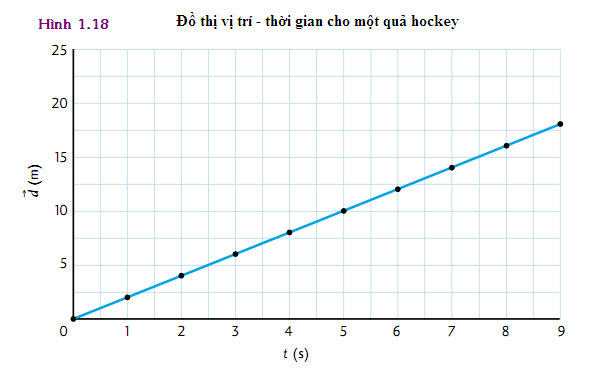
Hình 1.18 thể hiện đồ thị vị trí – thời gian cho cho một quả hockey lăn trên bàn băng. Ví dụ đơn giản này cho chúng ta một lượng thông tin đáng kể về chuyển động của vật. Nhắc lại rằng

Bằng cách tính độ dốc của đồ thị thẳng, ta có thể xác định vận tốc của quả hockey theo đơn vị m/s. Từ kết quả này, ta có thể kết luận rằng:
Độ dốc của đồ thị vị trí – thời gian cho biết vận tốc của vật.
Nếu như độ dốc của đồ thị vị trí – thời gian cho biết vận tốc, và chuyển động thẳng đều là vận tốc không đổi, thì đồ thị phải có độ dốc không đổi (tức là là một đường thẳng). Nói cách khác,
Nếu một vật đang chuyển động thẳng đều, thì đồ thị vị trí – thời gian của nó phải là một đường thẳng.
Không phải mọi đồ thị vị trí – thời gian đều là đường thẳng. Một số đồ thị là đường cong, và một số là sự kết hợp phức tạp của đường cong và đường thẳng. Không kể đến hình dạng của đồ thị, thì độ dốc của đồ thị vị trí – thời gian cho biết vận tốc của vật.
Hình 1.19 tóm tắt những thông tin ta có thể thu được từ đồ thị vị trí – thời gian.


Hình 1.20 thể hiện độ dốc của đường tiếp tuyến tại các điểm A và B trên một đồ thị vị trí – thời gian tăng dần. Tại điểm B, vận tốc của vật (tức là độ dốc của đường tiếp tuyến) lớn hơn tại điểm A. Đồ thị trên còn thể hiện một đường nối giữa A và B. Độ dốc của đường cát tuyến này cho chúng ta biết vận tốc trung bình giữa điểm A và B.
vtb = Δd/Δt
Vận tốc trung bình là độ dốc của đường nối hai điểm trên đồ thị vị trí – thời gian. Đối với những đồ thị vị trí – thời gian biểu diễn gia tốc không đổi, vận tốc tức thời của vật có thể xác định bằng cách tìm độ dốc của đường tiếp tuyến với đường cong đó.
Ví dụ 13. Độ dốc của đường tiếp tuyến trên đồ thị vận tốc – thời gian
Đồ thị trên Hình 1.21 biểu diễn chuyển động của một chiếc xe đồ chơi đang lao xuống dốc sau khi bộ phanh của nó đã hỏng. Sử dụng số liệu này, hãy xác định độ dốc của đường tiếp tuyến với đồ thị vị trí – thời gian tại bốn điểm. Sau đó, vẽ đồ thị vận tốc – thời gian tương ứng, và tìm độ dốc của nó. Xem chiều dương là hướng xuống dốc.

Bài giải và liên hệ lí thuyết
Khi ta tính độ dốc (tức là vận tốc) tại bốn điểm dọc theo đường cong trên Hình 1.22a, ta tìm thấy những giá trị này đang tăng lên. Một độ dốc đang tăng cho biết có sự gia tốc. Vì đồ thị vận tốc – thời gian là một đường thẳng (Hình 1.22c), nên ta biết gia tốc là không đổi.
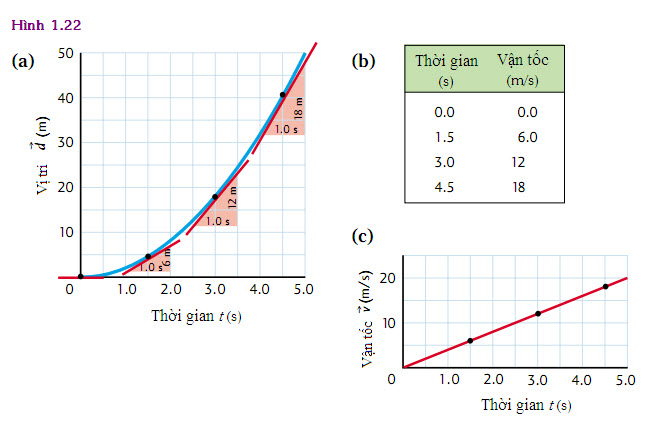
Giờ thì ta có thể tính độ dốc của đồ thị vận tốc – thời gian (Hình 1.22c):
độ dốc = độ tăng trên trục tung/độ tăng trên trục hoành
độ dốc = Δv/Δt
độ dốc = (18 m/s)/(4,5 s)
độ dốc = 4,0 m/s2 = gia tốc
Từ ví dụ này, ta xác định được rằng:
Độ dốc của một đồ thị vận tốc – thời gian thẳng là gia tốc không đổi của vật.
Tương tự như vậy,
Nếu đồ thị vận tốc – thời gian là một đường cong (Hình 1.22d), thì độ dốc của đường tiếp tuyến của nó tại bất kì điểm nào cho trước là gia tốc tức thời của vật.

Ta có thể học được những gì bằng cách tính diện tích nằm dưới một đồ thị vận tốc – thời gian? Hãy xét ví dụ sau đây:
Ví dụ 14. Diện tích nằm dưới đồ thị vận tốc – thời gian
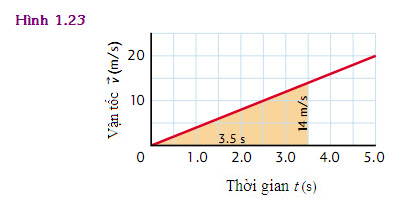
Diện tích nằm dưới đồ thị trên Hình 1.23 trong 3,5 s đầu tiên là bao nhiêu? (Hãy đảm bảo sử dụng đúng đơn vị)
Bài giải và liên hệ lí thuyết
Hình 1.23 là một đồ thị vận tốc – thời gian thẳng, tăng dần. Diện tích nằm dưới đồ thị này là một tam giác, nó bằng nửa cạnh đáy nhân với chiều cao:
A = ½ bh
A = ½ (3,5 s)(14 m/s)
A = 24 m
Đơn vị tạo ra trong ví dụ này là mét; vì vậy, ta có thể kết luận rằng
Diện tích nằm dưới đồ thị vận tốc – thời gian là độ dời của vật.
Tương tự,
Diện tích nằm dưới đồ thị gia tốc – thời gian là độ biến thiên vận tốc của vật.
Giả sử một vật bắt đầu chuyển động từ trạng thái nghỉ tại gốc tọa độ, ta có thể tóm tắt sự phân tích đồ thị của chuyển động thẳng trong một sơ đồ đơn giản:

Ví dụ 15. Đồ thị vận tốc – thời gian
1. Từ Hình 1.25, hỏi vận tốc tức thời của vật tại mỗi thời điểm sau đây bằng bao nhiêu?
t = 4,0 s
t = 8,0 s
t = 12 s
2. a) Gia tốc trung bình từ thời điểm t = 0 đến t = 4,0 s là bao nhiêu?
b) Gia tốc trung bình từ thời điểm t = 10 đến t = 15 s là bao nhiêu?
3. Gia tốc tức thời tại thời điểm t = 9,0 s là bao nhiêu?
4. Vật đã đi được bao xa trong 7,0 s đầu tiên?

Bài giải và liên hệ lí thuyết
- Ta có thể xác định vận tốc tức thời đơn giản bằng cách đọc ra nó từ đồ thị vận tốc – thời gian. Tại thời điểm t = 4,0 s, vận tốc là 2,0 m/s. Lúc t = 8,0 s, vận tốc là 5,0 m/s. Lúc t = 12 s, vận tốc là 1,0 m/s.
- Vì gia tốc được xác định bằng cách tính độ dốc của đồ thị vận tốc – thời gian, nên ta cần tìm độ dốc của đồ thị tại mỗi khoảng thời gian. Đối với
a. t = 0 đến t = 4,0 s
độ dốc = gia tốc = Δv/Δt
độ dốc = (2,0 m/s)/(4,0 s)
độ dốc = 0,50 m/s2
b. Từ t = 10 s đến t = 15 s, đồ thị là một đường dốc xuống. Do đó, ta sẽ có gia tốc âm:
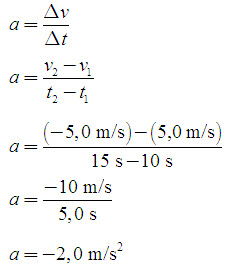
Gia tốc âm là cái đáng quan tâm vì hai nguyên do. Phía trên trục thời gian nằm ngang, gia tốc âm cho biết vật đang giảm tốc độ (tức là nó chuyển động chậm dần). Tại trục thời gian, vật có vận tốc bằng không và đứng yên trong khoảnh khắc. Cuối cùng, phía dưới trục thời gian, vật vẫn gia tốc theo chiều âm, nhưng tốc độ của nó đang tăng lên theo hướng ngược lại của chuyển động ban đầu (tức là vật tăng tốc ngược). Một ví dụ của loại chuyển động này, hãy xét một nhà du hành vũ trụ đang ở bên ngoài phi thuyền con thoi và đang đi tới nó với vận tốc 10 m/s [đông]. Để ngăn không để bản thân va chạm với phi thuyền con thoi, nhà du hành bật một động cơ tên lửa đẩy lùi từ kiện tên lửa của mình, bắn ra một lượng nhỏ chất khí nóng theo hướng đông. Nếu kiện tên lửa gây ra một gia tốc 1,0 m/s2 [tây], nhà du hành sẽ tiếp tục chuyển động chậm dần cho đến khi tạm dừng lại 10 s sau đó. Nếu lúc này, nhà du hành tắt kiện tên lửa, thì bà sẽ vẫn đứng yên. Nếu bà vô tình để tên lửa tiếp tục cháy, thì bà sẽ tiếp tục gia tốc theo hướng tây ngay sau khi tạm đứng yên. Vận tốc của nhà du hành sẽ tăng 1,0 m/s [tây] trong mỗi giây mà tên lửa đẩy lùi vẫn còn cháy.
3. Gia tốc tức thời tại thời điểm t = 9,0 s có thể tìm bằng cách xét đoán. Độ dốc của đồ thị vận tốc – thời gian cho biết gia tốc. Từ t = 7,0 s đến t = 9,0 s, độ dốc là nằm ngang, nghĩa là bằng không. Độ dốc bằng không có nghĩa là vật đang chuyển động thẳng đều.
4. Để xác định độ dời của vật, ta cần tìm diện tích nằm dưới đồ thị. Trong trường hợp này, ta có thể đơn giản hóa phép tính bằng cách chia diện tích đó thành nhiều tam giác và hình chữ nhật.

Vậy độ dời của vật trong 7,0 s đầu tiên là 14,5 m.
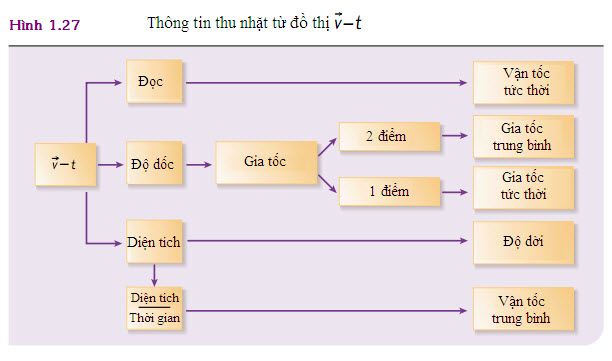
Hình 1.27 tóm tắt cách thu nhặt thông tin từ một đồ thị vận tốc – thời gian.

Vật lí - Các khái niệm và quan hệ
Nhiều tác giả
<< Phần trước | Phần tiếp theo >>