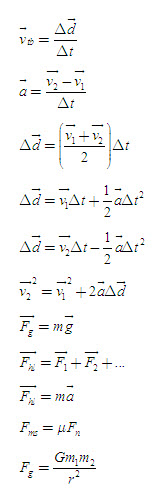2.1 Vector trong không gian hai chiều
Chúng ta chương 1, chúng ta đã biết vector là một đại lượng có cả độ lớn và chiều. Các vector có thể biểu diễn là những đoạn thẳng có chiều. Trong chương này, chúng ta sẽ sử dụng phép cộng vector và phép trừ vector để giải các bài toán.
Trong không gian hai chiều, chúng ta sẽ sử dụng các thành phần vô hướng trong các phương x và y. Như ở phần động học trong không gian một chiều, chúng ta sẽ kí hiệu chiều bằng dấu + và dấu –. Mũi tên vector sẽ không được sử dụng trừ khi nhắc tới một sơ đồ vector hay một đại lượng có cả độ lớn và chiều (thí dụ, d = 12 km [bắc30o đông]).
Cộng vector
Nếu hai vector vuông góc, ta có thể cộng chúng bằng định lí Pythagoras.
Ví dụ 1. Hai vector vuông góc
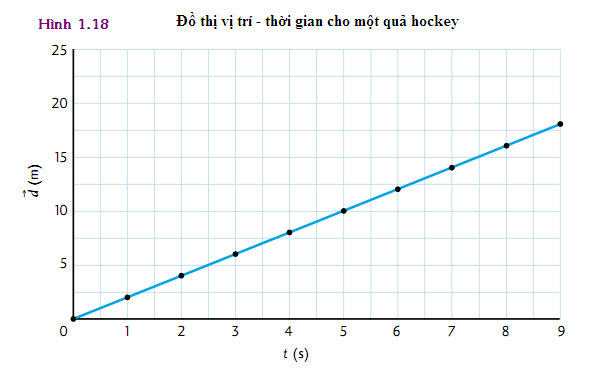
Một con kiến bò 10 cm [đông] trên một cái bàn picnic, sau đó rẽ hướng và bò thêm 15 cm [bắc]. Tính độ dời toàn phần của con kiến.
Bài giải và liên hệ lí thuyết
Cho biết

Đối với chiều của kết quả,

Từ định lí Pythagoras,

Chiều của vector này có thể biểu diễn là [đông30o nam] hoặc [nam60o đông], đọc là “hướng nam và quay 60o về phía đông”.
Ví dụ 2. Cộng hai vector khái quát trong không gian hai chiều
Một con thuyền đi 20 km [đông25o bắc], sau đó đi 45 km [bắc40o tây]. Tính độ dời toàn phần của con thuyền.
Bài giải và liên hệ lí thuyết
Cho biết
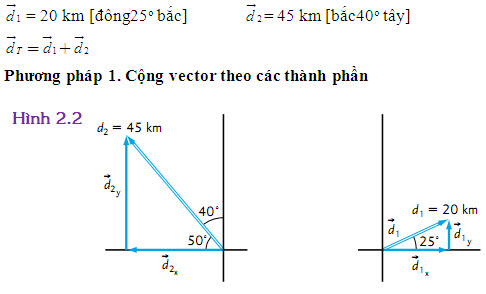
Sử dụng, hàm số cos, ta có thể mô tả d1x như sau:

Lưu ý chúng ta sử dụng bốn chữ số có nghĩa trong đáp số này để giảm sai số do làm tròn. Đáp số cuối cùng sẽ làm tròn đến hai chữ số có nghĩa giống như những số liệu đã cho.
Tổng vector của các thành phần y là

Để tìm độ lớn của độ dời, ta sử dụng định lí Pythagoras (Hình 2.3).
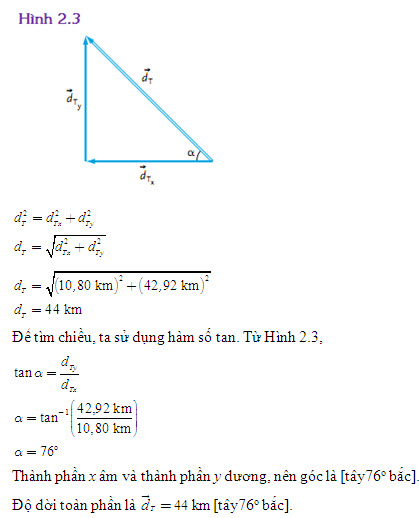
Phương pháp 2. Cộng vector bằng định lí hàm sin và cos


Đáp số này bằng đáp số ta thu được với phương pháp cộng các thành phần.
Các phương trình lượng giác
Trong Hình 2.4b, các góc của tam giác được kí hiệu bằng những kí tự in hoa, và những cạnh đối diện với chúng được kí hiệu bằng những kí tự in thường. Hễ khi nào chiều dài của hai cạnh và góc chứa (góc giữa chúng) đã biết, thì định lí cos được sử dụng,
c2 = a2 + b2 – 2ab cos C
Tương tự, nếu chúng ta biết giá trị của một góc, cạnh đối diện với nó, cùng với một góc hay một cạnh khác, ta có thể sử dụng định lí sin,

Hình 2.5 tóm tắt các bước giải bài toán cộng vector bằng phương pháp cộng các thành phần.

Vật lí - Các khái niệm và quan hệ
SGK của Canada - Nhiều tác giả
Bản dịch của Thuvienvatly.com
<< Phần trước | Phần tiếp theo >>