Vì sao E = mc2? - Phần 4

Để tìm chỗ hỏng trong câu trả lời của Aristotle, chúng ta hãy tạm chấp nhận bức tranh của ông và xem nó dẫn tới đâu. Theo Aristotle, chúng ta sẽ lấp đầy không gian với các đường lưới tưởng tượng có tâm trên Trái đất và vạch rõ cái gì tọa lạc ở đâu, và ai đang thực hiện chuyển động. Nếu chúng ta chấp nhận bức tranh này của không gian là một cái hộp chứa đầy các vật thể, với Trái đất tại tâm của nó, thì rõ ràng rằng bạn, người hành khách trên chiếc máy bay, đã thay đổi vị trí của bạn bên trong cái hộp đó, còn người quan sát bạn bay lướt qua thì đang đứng yên trên mặt đất, không thực hiện chuyển động trong không gian. Nói cách khác, có một cái đại loại là chuyển động tuyệt đối, và do đó có không gian tuyệt đối. Một vật là chuyển động tuyệt đối nếu nó thay đổi vị trí của nó trong không gian, khi đo trên mạng lưới tưởng tượng gắn với tâm Trái đất, khi thời gian tích tắc trôi qua.

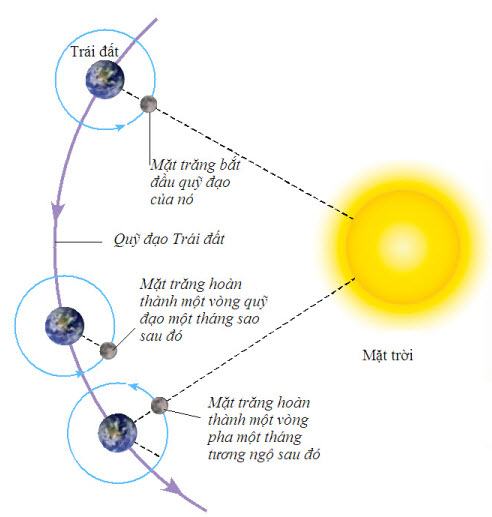
Một trở ngại với bức tranh này, tất nhiên, là Trái đất không hề đứng yên tại trung tâm của vũ trụ; nó là một quả cầu đang xoay tròn và quay xung quanh Mặt trời. Thật vậy, Trái đất đang chuyển động ở tốc độ khoảng 67.000 dặm trên giờ so với Mặt trời. Nếu đêm nay bạn lên giường và ngủ trong tám giờ, thì lúc thức dậy bạn đã đi được quãng đường hơn nửa triệu dặm. Bạn thậm chí có thể khẳng định rằng, trong khoảng 365 ngày, giường ngủ của bạn sẽ trở lại đúng ngay chỗ cũ trong không gian vì Trái đất vừa hoàn tất một vòng quỹ đạo xung quanh Mặt trời. Vì thế, bạn có thể quyết định thay đổi bức tranh của mình một chút, trong khi vẫn giữ nguyên vẹn tinh thần Aristotle. Tại sao không chọn tâm mạng lưới ở trên Mặt trời? Đó là một suy nghĩ đủ mức đơn giản, nhưng nó quá sai lầm vì bản thân Mặt trời đang quay xung quanh tâm của thiên hà Ngân hà. Dải Ngân hà là vũ trụ địa phương của chúng ta gồm hơn 200.000 triệu mặt trời, và như bạn có thể tưởng tượng nó rất lớn và mất khá nhiều thời gian để quay trọn một vòng. Mặt trời, cùng với Trái đất lai dắt theo, đang chuyển động xung quanh Ngân hà ở tốc độ 486.000 dặm trên giờ, ở cự li cách tâm quay 156.000 nghìn tỉ dặm. Ở tốc độ này, Mặt trời cần 226 triệu năm để quay trọn một vòng. Và như vậy, có lẽ cần tiến thêm một bước nữa là đủ để cứu lấy quan điểm Aristotle. Lấy tâm của mạng lưới là tâm của thiên hà Ngân hà của chúng ta, và bạn có thể đi tới một suy nghĩ liên tưởng khác: Khi bạn nằm trên giường, hãy tưởng tượng thế giới trông như thế nào lúc gần đây nhất Trái đất tọa lạc “tại đây”, tại chính xác điểm này trong không gian. Một con khủng long đang ngắm nhìn bóng bình minh, ăn những chiếc lá thời tiền sử tại chỗ chiếc giường của bạn bây giờ. Lại sai nữa rồi. Thật vậy, bản thân các thiên hà đang chạy ra xa nhau, và các thiên hà ở càng xa thì chúng lùi ra xa chúng ta càng nhanh. Chuyển động của chúng ta giữa vô số thiên hà cấu tạo nên vũ trụ có vẻ thật sự cực kì khó xác định được.

Vì thế Aristotle gặp vướng mắc, bởi vì dường như không thể nào định nghĩa chính xác ý nghĩa của từ “đứng yên” là gì. Nói cách khác, có vẻ như chẳng thể nào xác định chỗ nào là tâm của mạng lưới tưởng tượng mà chúng ta có thể xác định chỗ của các vật ở trên đó, và do đó xác định cái gì đang đứng yên và cái gì đang chuyển động. Bản thân Aristotle chưa từng phải đối mặt với vấn đề này bởi vì bức tranh của ông về một Trái đất tĩnh tại được vây quanh bởi những quả cầu quay tròn đã không bị thách thức gì nhiều trong gần như 2000 năm trời. Có lẽ, như chúng ta đã nói, những cái này là quá hiển nhiên, ngay cả với những trí tuệ lỗi lạc nhất. Claudius Ptolemaeus, ngày nay gọi là Ptolemy, đã làm việc trong đại thư viện Alexandria ở Ai Cập hồi thế kỉ thứ hai. Ông là một nhà quan sát tỉ mỉ của bầu trời đêm, và ông lo ngại về chuyển động biểu kiến lạ lùng trên bầu trời của năm hành tinh đã biết khi ấy, hay các “tinh cầu lang thang”, từ đó mới có tên gọi “hành tinh”. Khi quan sát từ Trái đất trong nhiều tháng, các hành tinh không đi theo quỹ đạo trơn trên nền trời sao, mà có vẻ tiến hành thắt nút trên bầu trời. Chuyển động kì lạ này được gọi là chuyển động thụt lùi, và đã được biết tới từ hàng nghìn năm trước thời Ptolemy. Người Ai Cập xưa mô tả sao Hỏa là hành tinh “đi ngược”. Ptolemy đồng ý với Aristotle rằng các hành tinh đang quay xung quanh Trái đất đứng yên, nhưng để giải thích chuyển động thụt lùi ông buộc phải gắn chúng với những bánh xe quay lệch tâm nhỏ hơn nữa, rồi mới gắn chúng với những quả cầu đang chuyển động. Mô hình khá phức tạp này có thể giải thích chuyển động của các hành tinh trên bầu trời đêm, mặc dù nó không đẹp cho lắm. Lời giải thích đúng cho chuyển động thụt lùi của các hành tinh phải chờ đến tận giữa thế kỉ 17 và Nicholas Copernicus, người đề xuất lời giải thích đẹp hơn (và chính xác hơn) rằng Trái đất không phải đứng yên tại trung tâm của vũ trụ, mà thật ra đang quay xung quanh Mặt trời cùng với các hành tinh còn lại. Công trình của Copernicus không phải không bị gièm pha bêu xấu và nó chỉ được đưa ra khỏi danh sách cấm của Giáo hội Thiên chúa vào năm 1835. Những phép đo chính xác được thực hiện bởi Tycho Brahe, cùng với công trình của Johannes Kepler, Galileo, và Newton, cuối cùng đã chứng minh không những Copernicus là đúng, mà còn đưa đến một lí thuyết của chuyển động hành tinh ở dạng các định luật Newton của chuyển động và lực hấp dẫn. Những định luật đó vẫn trụ vững là bức tranh tốt nhất của chúng ta của chuyển động của các hành tinh và thật ra là chuyển động của tất cả mọi vật thể dưới tác dụng của lực hấp dẫn, từ các thiên hà đang quay tròn cho đến đạn pháo, cho đến khi thuyết tương đối rộng của Einstein ra đời vào năm 1915.

Phần tiếp theo >>

Bài trước | Bài kế tiếp