Cơ sở vật lí - Phần 1

C H Ư Ơ N G 1  

Đo lường

1 – 1 ĐO LƯỜNG, ĐO ĐỘ DÀI

Mục tiêu

Nội dung chính

• Vật lí học được xây dựng trên đo lường các đại lượng vật chất. Những đại lượng vật lí nhất định được chọn làm đại lượng cơ bản (ví dụ độ dài, thời gian, và khối lượng); mỗi đại lượng được định nghĩa theo một chuẩn nào đó và được gán một đơn vị đo (ví dụ mét, giây, và kilogram). Những đại lượng vật lí khác được định nghĩa theo các đại lượng cơ bản và các chuẩn của chúng cùng các đơn vị.
• Hệ đơn vị được nhấn mạnh trong quyển sách này là Hệ Đơn vị Quốc tế (SI). Ba đại lượng vật lí trình bày trong Bảng 1.1 được sử dụng trong các chương đầu. Các tiêu chuẩn thiết lập cho các đại lượng này, chúng phải vừa truy xuất được vừa bất biến, đã được quốc tế thống nhất. Các tiêu chuẩn này được sử dụng cho mọi phép đo vật lí, cho các đại lượng cơ bản lẫn các đại lượng dẫn xuất từ chúng. Kí hiệu khoa học và các tiếp ngữ của Bảng 1.2 được sử dụng để đơn giản hóa kí hiệu đo lường.
• Việc đổi đơn vị có thể được thực hiện bằng cách sử dụng các xích-liên kết trong đó số liệu ban đầu được nhân liên tiếp với các hệ số chuyển đổi được viết dưới dạng đơn vị và các đơn vị được thao tác giống như các đại lượng vật lí, chỉ giữ lại các đơn vị như mong muốn.
• Mét được định nghĩa là quãng đường mà ánh sáng đi được trong một khoảng thời gian chính xác nhất định.

Vật lí là gì?

Khoa học và kĩ thuật được xây dựng trên đo lường và so sánh. Vì thế, ta cần các quy tắc cho biết các thứ được đo và so sánh như thế nào, và ta cần các thí nghiệm để xác lập đơn vị cho các phép đo và so sánh đó. Một mục tiêu của vật lí học (và kĩ thuật) là thiết kế và xây dựng những thí nghiệm đó.

Chẳng hạn, các nhà vật lí phấn đấu phát triển các đồng hồ cực kì chuẩn xác để mọi thời điểm hay khoảng thời gian có thể được xác định và so sánh thật chính xác. Bạn có thể tự hỏi sự chuẩn xác như thế thật sự có cần thiết và đáng để ta nỗ lực hay không. Đây là thí dụ cho thấy sự đáng giá ấy: Không có các đồng hồ cực kì chuẩn xác, Hệ thống Định vị Toàn cầu (GPS) thiết yếu cho việc đi lại trong thế giới ngày nay sẽ không hoạt động được.

Đo lường

Ta khám phá thế giới vật lí bằng cách học cách đo các đại lượng có liên quan trong vật lí học. Trong số những đại lượng này là độ dài, thời gian, khối lượng, nhiệt độ, áp suất, và cường độ dòng điện.

Ta đo mỗi đại lượng vật lí theo đơn vị riêng của nó, bằng cách so sánh với một chuẩn đo. Đơn vị là tên gọi độc nhất mà ta gán cho số đo của đại lượng đó, ví dụ, mét (m) cho đại lượng độ dài. Chuẩn đo ứng với đúng 1,0 đơn vị của đại lượng đó. Như bạn sẽ thấy, chuẩn đo cho độ dài, ứng với đúng 1,0 m, là quãng đường mà ánh sáng đi được trong chân không trong một phần nhỏ xác định của một giây. Ta có thể định nghĩa một đơn vị và chuẩn của nó theo bất cứ cách nào mà ta quan tâm. Tuy nhiên, điều quan trọng là định nghĩa theo kiểu sao cho các nhà khoa học trên toàn thế giới sẽ tán thành định nghĩa của ta là vừa có tính nhận thức vừa có tính thực tiễn.

Một khi ta đã thiết lập một chuẩn đo – nói thí dụ, cho độ dài – ta phải chỉ rõ các thủ tục mà theo đó bất kì độ dài nào, dù nó là bán kính của một nguyên tử hydrogen, độ dài trục của xe trượt tuyết, hay khoảng cách đến một ngôi sao, có thể được biểu diễn theo chuẩn đó. Các thước đo, lấy gần đúng chuẩn độ dài của ta, cho ta một thủ tục như thế để đo độ dài. Tuy nhiên, nhiều so sánh của ta phải là gián tiếp. Bạn không thể sử dụng một cái thước, chẳng hạn, để đo bán kính của một nguyên tử hay khoảng cách đến một ngôi sao.

Các đại lượng cơ bản. Có quá nhiều đại lượng vật lí nên việc tổ chức chúng là cả một vấn đề. May thay, chúng không hoàn toàn độc lập nhau; thí dụ, tốc độ là tỉ số của độ dài với thời gian. Như vậy, cái ta phải làm là chỉ ra – theo thỏa thuận quốc tế – một số lượng nhỏ những đại lượng vật lí, ví dụ độ dài và thời gian, và gán riêng chuẩn cho chúng. Khi đó, ta định nghĩa tất cả những đại lượng vật lí khác theo những đại lượng cơ bản này và chuẩn của chúng (gọi là chuẩn cơ bản). Thí dụ, tốc độ được định nghĩa theo các đại lượng cơ bản độ dài và thời gian và các chuẩn cơ bản của chúng.

Các chuẩn cơ bản phải vừa truy xuất được vừa bất biến. Nếu ta định nghĩa chuẩn độ dài là khoảng cách giữa mũi và ngón trỏ trên cánh tay giang thẳng của một người, thì chắc chắn ta có một chuẩn có thể truy xuất – nhưng tất nhiên nó sẽ biến thiên tùy theo người. Nhu cầu chính xác trong khoa học và kĩ thuật thúc đẩy ta ưu tiên hướng tới tính bất biến. Sau đó, ta có thể nỗ lực tạo ra bản sao của các chuẩn cơ bản truy xuất được cho những ai cần đến chúng.

Hệ Đơn vị Quốc tế

Vào năm 1971, Hội nghị Toàn thể về Cân nặng và Đo lường lần thứ 14 đã chọn bảy đại lượng làm đại lượng cơ bản, từ đó tạo nên cơ sở của Hệ Đơn vị Quốc tế, viết tắt SI từ tên gọi tiếng Pháp của nó và thường được gọi là hệ mét. Bảng 1-1 giới thiệu đơn vị cho ba đại lượng cơ bản – độ dài, khối lượng, và thời gian – mà ta sử dụng ở các chương đầu của quyển sách này. Các đơn vị này được định nghĩa trên một “thang bậc con người”.

Nhiều đơn vị dẫn xuất SI được định nghĩa theo các đơn vị cơ bản này. Thí dụ, đơn vị SI cho công suất, gọi là watt (W), được định nghĩa theo ba đơn vị cơ bản cho khối lượng, độ dài, và thời gian. Vì thế, như bạn sẽ thấy trong Chương 7,

1 watt = 1 W = 1 kg . m²/s³,                            (1-1)

trong đó tập hợp các kí hiệu đơn vị sau cùng đọc là kilogram-mét bình phương trên giây lũy thừa ba.

Để biểu diễn những đại lượng rất lớn và rất nhỏ mà ta thường gặp trong vật lí học, ta sử dụng kí hiệu khoa học, được viết theo lũy thừa của 10. Trong kí hiệu này,

3 560 000 000 m = 3,56 × 10⁹ m                    (1-2)

và                    0,000 000 492 s = 4,92 × 10 ^{– 7} s.                    (1-3)

Kí hiệu khoa học trên máy tính đôi khi trông còn ngắn gọn hơn, như 3,56 E9 và 4,92 E –7, trong đó E là viết tắt cho “lũy thừa của 10”. Một số máy tính bỏ túi còn hiển thị ngắn gọn hơn nữa, trong đó E được thay bằng một khoảng trống.

            Một tiện lợi nữa khi xử lí các số đo rất lớn hay rất nhỏ, ta sử dụng các tiếp ngữ được liệt kê trong Bảng 1-2. Như bạn có thể thấy, mỗi tiếp ngữ biểu diễn một lũy thừa nhất định của 10, được dùng như một hệ số nhân. Việc gắn một tiếp ngữ với một đơn vị SI có tác dụng nhân với thừa số đi kèm. Như vậy, ta có thể biểu diễn một công suất điện nhất định là

1,27 × 10⁹ watt = 1,27 gigawatt = 1,27 GW              (1-4)

hay một khoảng thời gian nhất định là

2,35 × 10 ^{– 9} s = 2,35 nano giây = 2,35 ns                   (1-5)

Một số tiếp ngữ, như dùng trong milli-mét, centi-mét, kilogram, và megabyte, có lẽ là quen thuộc với bạn.

Đổi đơn vị

Chúng ta thường cần chuyển đổi đơn vị trong đó một đại lượng vật lí được biểu diễn. Ta đổi bằng một phương pháp gọi là biến đổi xích-liên kết. Trong phương pháp này, ta nhân số đo ban đầu với một hệ số chuyển đổi (một tỉ số của các đơn vị bằng đơn vị). Thí dụ, vì 1 min và 60 s là những khoảng thời gian y hệt nhau, nên ta có

Như vậy, các tỉ số (1 min)/(60 s) và (60 s)/(1 min) có thể được dùng làm hệ số chuyển đổi. Trình bày như vậy không giống với viết 1/60 = 1 hay 60 = 1; mỗi con số và đơn vị của nó phải được xử lí chung với nhau.

            Vì nhân một đại lượng bất kì với đơn vị cho đại lượng đó không đổi, nên ta có thể đưa hệ số chuyển đổi vào bất cứ chỗ nào ta thấy có ích. Trong phép biến đổi xích-liên kết, ta sử dụng các hệ số để triệt tiêu các đơn vị không mong muốn. Thí dụ, để đổi 2 min sang giây, ta có

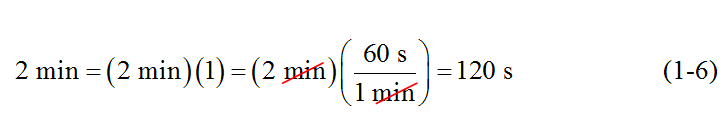
Phụ lục D cung cấp hệ số chuyển đổi giữa hệ SI và các hệ đo lường khác, trong đó có các đơn vị phi SI vẫn được sử dụng ở nước Mĩ. Tuy nhiên, các hệ số chuyển đổi được viết theo kiểu “1 min = 60 s” thay cho cách viết tỉ số. Do đó, bạn cần xác định rõ tử số và mẫu số trong bất kì tỉ số cần thiết nào.

độ dài

Vào năm 1792, nước Cộng hòa Pháp mới ra đời đã cho thiết lập một hệ thống cân đo mới. Nền tảng của nó là mét, được định nghĩa là một phần mười triệu của khoảng cách từ cực Bắc đến xích đạo. Sau đó, vì các lí do thực tế, chuẩn Trái đất này bị vứt bỏ và mét được định nghĩa là khoảng cách giữa hai vạch mảnh khắc gần hai đầu của một thanh platinum-iridium, thanh mét chuẩn, được lưu giữ tại Cục Cân Đo Quốc tế ở gần Paris. Các bản sao chính xác của thanh mét được gửi đến các phòng thí nghiệm chuẩn hóa trên khắp thế giới. Các chuẩn thứ cấp này được sử dụng để tạo ra các chuẩn khác nữa, vẫn là các chuẩn truy xuất được, sao cho cuối cùng thì mỗi dụng cụ đo có hiệu lực của nó từ thanh mét chuẩn qua một chuỗi so sánh phức tạp.

Cuối cùng, một chuẩn chính xác hơn khoảng cách giữa hai vạch khắc mảnh trên một thanh kim loại là cần thiết. Vào năm 1960, một chuẩn mới cho mét, dựa trên bước sóng ánh sáng, đã được phê chuẩn. Đặc biệt, chuẩn cho mét được định nghĩa là bằng 1 650 763,73 bước sóng của một ánh sáng màu cam-đỏ xác định được phát ra bởi các nguyên tử krypton-86 (một đồng vị, hay một loại, krypton đặc biệt) trong một ống phóng điện khí có thể được triển khai ở bất cứ nơi nào trên thế giới. Con số bước sóng bất tiện này được chọn sao cho chuẩn mới sẽ gần với chuẩn thanh-mét cũ.

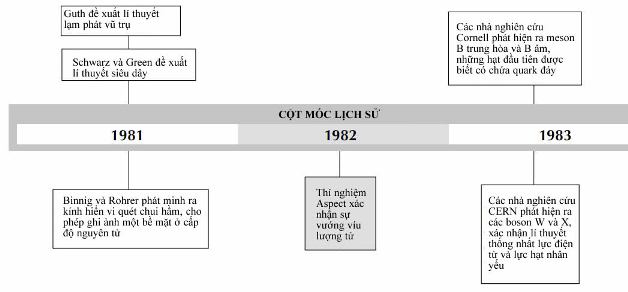
Tuy nhiên, vào năm 1983, yêu cầu độ chính xác cao đã đạt tới mức mà ngay cả chuẩn krypton-86 cũng không đáp ứng nỗi, và vào năm ấy đã diễn ra một bước tiến quan trọng. Mét được định nghĩa lại là quãng đường mà ánh sáng đi được trong một khoảng thời gian xác định. Theo ngôn từ của Hội nghị Toàn thể về Cân nặng và Đo lường lần thứ 17 thì

Khoảng thời gian này được chọn sao cho tốc độ ánh sáng c chính xác bằng

c = 299 792 458 m/s.

            Các phép đo tốc độ ánh sáng đã trở nên cực kì chính xác, cho nên người ta phê chuẩn tốc độ ánh sáng là một đại lượng đã được định nghĩa và sử dụng nó để định nghĩa lại mét.

            Bảng 1-3 trình bày một ngưỡng rộng của các độ dài, từ kích cỡ của vũ trụ (hàng trên cùng) đến kích cỡ của một số vật rất nhỏ.

Số chữ số có nghĩa và Vị trí dấu phẩy

Giả sử bạn giải một bài toán trong đó mỗi giá trị bao gồm hai chữ số. Các chữ số đó được gọi là chữ số có nghĩa và chúng đặt ra số chữ số mà bạn có thể sử dụng lúc đưa ra đáp số cuối cùng của bạn. Với số liệu đã cho bằng hai chữ số có nghĩa, đáp số cuối cùng của bạn nên chỉ có hai chữ số có nghĩa. Tuy nhiên, tùy thuộc vào thiết lập mode trên máy tính bỏ túi của bạn, nhiều chữ số có nghĩa hơn có thể được hiển thị. Các chữ số hiển thị thêm đó là vô nghĩa.

Trong quyển sách này, kết quả cuối cùng của các phép tính thường được làm tròn cho khớp với số chữ số có nghĩa tối thiểu trong số liệu đã cho. (Tuy nhiên, thỉnh thoảng thêm một chữ số có nghĩa nữa được giữ lại.) Khi tận cùng bên trái của các chữ số bị bỏ đi là 5 hoặc lớn hơn, thì chữ số cuối cùng còn lại được làm tròn lên; ngược lại thì nó được giữ nguyên. Thí dụ 11,3516 được làm tròn đến ba chữ số có nghĩa là 11,4 và 11,3279 được làm tròn đến ba chữ số có nghĩa là 11,3. (Đáp số cho các bài toán mẫu trong quyển sách này thường được trình bày với kí hiệu = thay vì » cho dù nó có được làm tròn hay không.)

Khi một con số như 3,15 hoặc 3,15 × 10³ được cho trong một bài toán, thì số chữ số có nghĩa là rõ ràng, nhưng còn con số 3000 thì sao? Phải chăng nó chỉ được biết với một chữ số có nghĩa (3 × 10³)? Hay là nó được biết đến bốn chữ số có nghĩa (3,000 × 10³)? Trong quyển sách này, ta giả sử rằng toàn bộ các số không trong các số đã cho như 3000 là có nghĩa, nhưng tốt hơn bạn không nên sử dụng giả định đó ở chỗ khác.

Đừng nhầm số chữ số có nghĩa với số chữ số phần thập phân. Xét các độ dài 35,6 mm; 3,56 m; và 0,00356 m. Chúng đều có ba chữ số có nghĩa, nhưng chúng lần lượt có một, hai, và năm chữ số thập phân.

Ví dụ mẫu 1.01 Ước tính bậc độ lớn, quả bóng dây

Quả bóng dây lớn nhất thế giới có bán kính khoảng 2 m. Lấy đến bậc độ lớn gần nhất, thì tổng độ dài L của sợi dây trong quả bóng bằng bao nhiêu?

Ý TƯỞNG GIẢI

Tất nhiên, ta có thể tách quả bóng ra và đo tổng độ dài L, nhưng như thế sẽ tốn nhiều công sức và khiến người chế tạo quả bóng rất không hài lòng. Thay vậy, bởi vì ta chỉ cần bậc độ lớn gần nhất, nên ta có thể ước tính bất cứ đại lượng nào cần thiết trong tính toán.

Tính toán: Ta giả sử quả bóng có dạng hình cầu với bán kính R = 2 m. Sợi dây trong quả bóng không bị ép chặt (có vô số khoảng trống giữa các đoạn liền kề của sợi dây). Để cho phép những khoảng trống này, ta hãy ước tính cao hơn chút ít diện tích mặt cắt của sợi dây bằng cách giả sử tiết diện đó là hình vuông, với độ dài một cạnh là d = 4 mm. Khi đó, với tiết diện d² và độ dài L thì sợi dây chiếm một thể tích toàn phần là

V = (tiết diện)(độ dài) = d²L

Thể tích này xấp xỉ bằng thể tích của quả bóng, được cho bởi 4/3πR³, tức là khoảng 4R³, vì p xấp xỉ bằng 3. Như vậy, ta có như sau

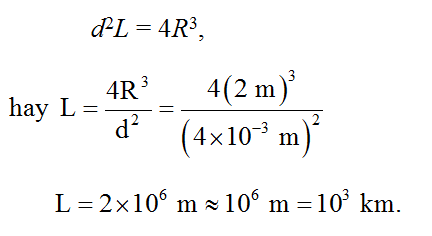
(Đáp số)

(Lưu ý rằng bạn không cần dùng đến máy tính bỏ túi cho một phép tính đơn giản như thế này.) Tính đến bậc độ lớn gần nhất, quả bóng chứa khoảng 1000 km dây!

CƠ SỞ VẬT LÍ
Halliday & Resnick – Jearl Walker
Bản in lần thứ 10
Bản dịch của Thuvienvatly.com
Phần tiếp theo >>