Alfred B. Bortz
Các hạt cơ bản và các lực cơ bản
Có lẽ xu hướng nổi trội nhất của ngành vật lí thập niên 1960 là việc định nghĩa lại các hạt nào và lực nào được xem là cơ bản. Kể từ thời Newton, các nhà vật lí đã hiểu rằng những vật thể lớn bị hút lại với nhau bởi sự hấp dẫn, một lực tác dụng lên khối lượng của các vật. Việc tìm hiểu sự hấp dẫn cho phép họ tìm hiểu động lực học của hệ mặt trời. Vào thế kỉ thứ 19, họ bắt đầu tìm hiểu các lực điện từ. Vào đầu thế kỉ 20, họ hiểu được rằng các nguyên tử cùng những hạt thành phần của chúng mang điện tích và từ tính, và rằng lực điện tác dụng lên điện tích của các electron và hạt nhân để giữ chúng lại với nhau bên trong các nguyên tử. Nó cũng liên kết các nguyên tử lại với nhau thành các phân tử và, với lực từ đồng hành của nó, là cơ sở của năng lượng ánh sáng. Khi các nhà vật lí bắt đầu tìm hiểu sự phóng xạ, họ nhận ra hai lực tác dụng bên trong hạt nhân, nhưng họ không thể nhận ra ngay những tính chất vật lí tương ứng với khối lượng và điện tích mà những lực đó tác dụng lên. Họ cũng nêu ra câu hỏi sau đây: Có phải bốn lực đó – lực hấp dẫn, lực điện từ, tương tác hạt nhân mạnh và yếu – là tất cả những gì tự nhiên phải có, và có nên xem chúng là cơ bản hay không? Nghiên cứu trong thập niên 1960 sẽ đưa các nhà vật lí đi đến những câu trả lời bất ngờ cho câu hỏi đó, chúng được mô tả ở cuối phần này và trong chương 8.
Những câu hỏi đại loại như vậy cũng đang xuất hiện trong thế giới hạ nguyên tử. Trong thế kỉ 19, các nhà vật lí và hóa học nghĩ tới các nguyên tử là những viên gạch cấu trúc cơ bản của vật chất. Sau đó, vào những năm cuối của thế kỉ 19, các khám phá về sự phóng xạ và electron, hạt hạ nguyên tử đầu tiên được biết tới, đã nêu lên vấn đề phải định nghĩa lại sự cơ bản. Nghiên cứu trong ba thập niên đầu của thế kỉ 20 sớm loại đi mọi nghi ngờ: Với việc khám phá ra hạt nhân nguyên tử và các hạt thành phần của nó, proton và neutron, các nhà vật lí đã chứng minh được rằng có những thực thể còn cơ bản hơn cả các nguyên tử. Ngoài proton, neutron và electron, vào giữa thập niên 1930, các nhà vật lí còn tin rằng neutrino cũng là một bộ phận của bảng kê các hạt hạ nguyên tử, mặc dù nó không được phát hiện ra về mặt thực nghiệm mãi cho đến năm 1956.
Vào thập niên 1960, do danh sách mở rộng dần của các hạt hạ nguyên tử, nhiều hạt trong số đó dường như không thuộc về các nguyên tử, nên lại nổi lên một câu hỏi mới. Những hạt nào trong số đó nên xem là cơ bản, và những hạt nào còn cấu tạo gồm những hạt nhỏ hơn nữa? Lí thuyết lực mạnh của Yukawa cho các pion một chỗ đứng bên trong hạt nhân. Nhưng còn muon, kaon và các hạt lạ mới phát hiện trong những năm 1950 thì phù hợp với những chỗ nào trong khuôn khổ nguyên tử? Một trong nhiều nhà vật lí bắt đầu nhận ra rằng “hạ nguyên tử” không đồng nghĩa với “cơ bản” là Murray Gell-Mann ở Caltech. Giống như Mendeleyev đã làm khi phát triển bảng tuần hoàn các nguyên tố hóa học, Gell-Mann và những người khác bắt đầu tìm kiếm những khuôn mẫu trong tính chất của các hạt trong “vườn bách thú” hạ nguyên tử. Nếu họ có thể tìm ra một khuôn mẫu, thì họ có thể luận ra cơ sở cho nó, giống như các tính chất của proton, neutron và electron trong các nguyên tử cuối cùng đã giải thích cho những khuôn mẫu mà Mendeleev đã tìm thấy trong số các tính chất của các nguyên tố hóa học.
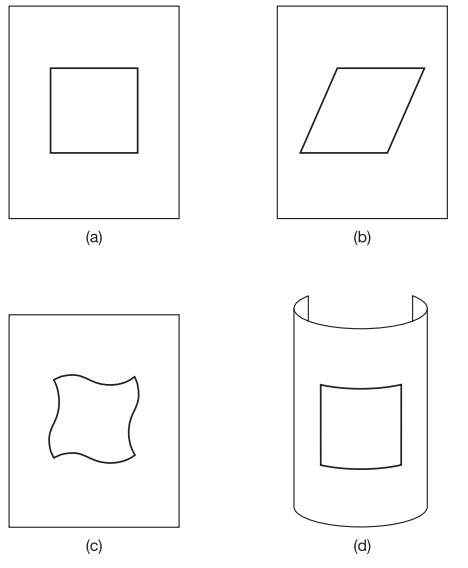
Một phương pháp yêu thích đối với các nhà vật lí là đi tìm các đối xứng toán học. Những đối xứng này liên quan đến những toán tử toán học thực hiện trên một hệ tạo ra một trạng thái trông y hệt sau khi tác dụng giống như nó đã thực hiện trước đó. Thí dụ, trong mô tả các tính chất lượng tử của chất kết tinh, các nhà vật lí đã viện đến sự đối xứng tịnh tiến, hay sự đối xứng của chuyển động theo một hướng đặc biệt. Họ mô tả tinh thể là một sự lặp lại vô hạn của các ô đơn vị trong không gian ba chiều. Khi họ áp dụng các phương trình của vật lí lượng tử, thì hàm sóng thu được tại một điểm bất kì trong một ô đơn vị phải giống như tại điểm tương đương trong bất kì ô nào khác. Đó là đối xứng tịnh tiến, và áp dụng của nó trong cơ học lượng tử của các chất rắn dẫn đến những ý tưởng hữu ích như các dải hóa trị và dải dẫn cho các electron và các khe năng lượng giữa chúng.
Một đối xứng quen thuộc nữa là đối xứng quay. Một lần nữa, các tinh thể cung cấp một phương pháp hữu dụng để tìm hiểu hiện tượng này. Đối xứng quay đòi hỏi một trục đối xứng, xung quanh đó tinh thể quay tròn. Nếu các ô đơn vị là những hộp lập phương, thì việc quay tinh thể đi một phần tư vòng tròn xung quanh một trục đi qua cạnh của một ô mang lại một cấu hình giống hệt như điểm xuất phát. Sự đối xứng đó được gọi là đối xứng quay bậc bốn. Nếu các ô đơn vị là những khối rắn tam giác chứ không phải lập phương, thì kiểu mẩu lặp lại sau một chuyển động quay nửa vòng tròn – đối xứng bậc hai.
Một loại đối xứng nữa là đối xứng phản xạ - giống như một ảnh qua gương. Đối xứng đó không đơn giản như trông nó thế, vì các chuyển động quay không phản xạ theo kiểu giống nhau như chuyển động thẳng. Người ta định nghĩa bốn điểm định vị chính trên Trái đất sao cho hướng đông là hướng mặt trời mọc, và các hướng theo chiều kim đồng hồ là bắc-đông-nam-tây. Đó được xem là cấu hình thuận, vì nếu các ngón tay của bàn tay phải uốn cong theo chiều quay của hành tinh, thì lòng bàn tay chỉ hướng bắc. Một cách hình dung khác là hãy tưởng tượng đang từ vũ trụ nhìn xuống địa cực của hành tinh đang quay ngược chiều kim đồng hồ. Địa cực đang nhìn đó phải là cực bắc. Hành tinh ảnh qua gương sẽ quay theo chiều kim đồng hồ, nghĩa là hoặc địa cực đang nhìn là cực nam, hoặc là thứ tự hướng bắc-đông-nam-tây là ngược chiều kim đồng hồ, một thế giới nghịch. Hình vẽ ở trang sau hướng nghịch của hành tinh Trái đất và ảnh qua gương của nó.
Ở cấp độ lượng tử, spin của một hạt không phải là chuyển động quay thật sự, mà là nó hành xử về mặt toán học giống như thế. Khi số lượng tử spin được đưa vào các phương trình lượng tử mô tả các electron trong nguyên tử, thì kết quả là nguyên lí loại trừ Pauli nổi tiếng! Điều đó chứng minh sự đối xứng quan trọng như thế nào trong vật lí học.
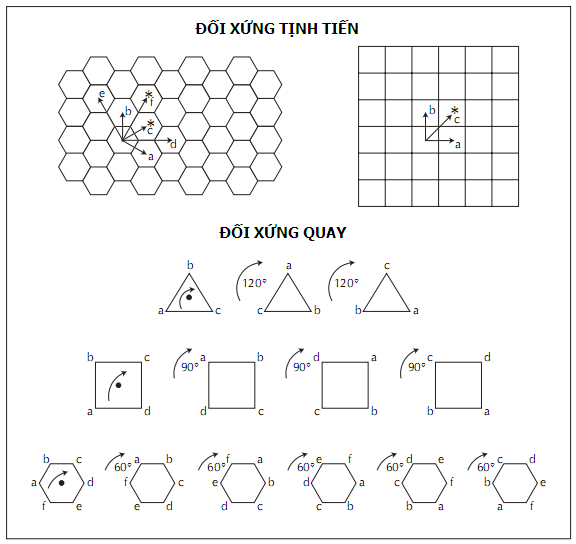
Các nhà vật lí đi tìm sự đối xứng trong tự nhiên, thí dụ như đối xứng (chuyển động) tịnh tiến và đối xứng quay của các cấu trúc tinh thể, và sử dụng nó trong mô tả toán học của họ cho các hiện tượng tự nhiên.
Sự đối xứng toán học không chỉ áp dụng cho hình học, mà còn cho bất kì đại lượng vật lí nào có thể biểu diễn trên đồ thị. Gell-Mann là một trong những nhà vật lí đầu tiên áp dụng các ý tưởng đối xứng cho các hạt hạ nguyên tử. Ông đặt proton, neutron và các baryon khác lên trên một đồ thị với số lượng tử lạ trên trục đứng và một số lượng tử khác gọi là isospin trên trục ngang. Tên gọi isospin phản ánh tính chất hành xử khi đặt trước sự phản xạ toán học; đó là, theo kiểu giống như chuyển động quay hoặc một cặp cực từ. Đối với lực hạt nhân mạnh (không tác dụng lên khối lượng hay điện tích), các proton và neutron là những hạt giống nhau với số lượng tử isospin ngược dấu (- ½ cho neutron, + ½ cho proton). Kết quả, như minh họa trong giản đồ ở trên, là một biểu đồ với một loại đối xứng gọi là SU(2). SU là viết tắt của cụm từ “nhất thể đặc biệt”, kết hợp đối xứng quay và đối xứng phản xạ. Số 2 có nghĩa là đối xứng quay là bậc hai. Nếu các hạt trên biểu đồ quay đi nửa vòng tròn thì isospin được thay thế bởi ảnh qua gương của nó (thí dụ, proton trở thành neutron, và ngược lại), kết quả giống y hệt như hình ban đầu.
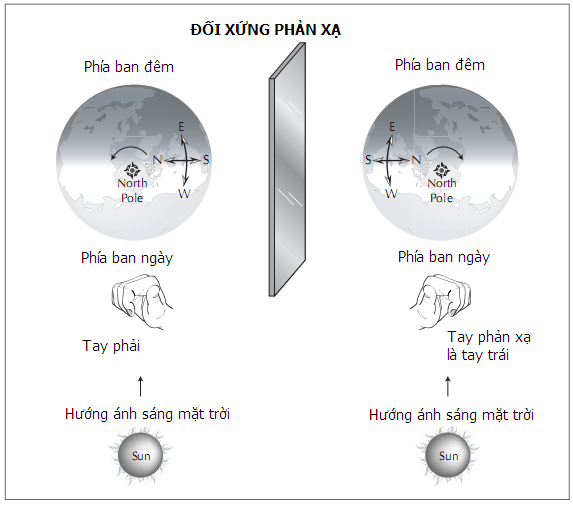
Sự phản xạ tạo ra một loại đối xứng khác đảo lộn bên trái với bên phải trong các hiện tượng giống như chuyển động quay.
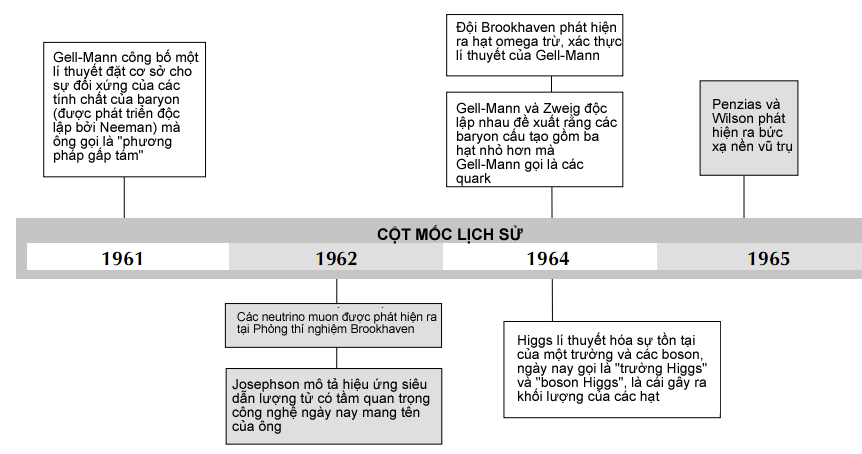
Nói cách khác, đối xứng SU(2) đã cho phép Gell-Mann tổ chức các hạt hạ nguyên tử thành những nhóm tám – hay octet – thí dụ như trong biểu đồ bên dưới: Proton và neutron có số lạ 0 và isospin ½ (trạng thái lượng tử được phép cho proton là + ½, và cho neutron là – ½); hạt lambda trung hòa số lạ 1 và isospin 0; hạt sigma có số lạ - 1 và isospin 1 (cho phép ba trạng thái lượng tử, - 1, 0, + 1, tương ứng với hạt sigma âm, trung hòa, và sigma dương); và hạt xi có số lạ -2 và isospin ½ (cho phép trạng thái lượng tử ± ½ , tương ứng với xi âm và xi trung hòa). Khi ông công bố lí thuyết của mình vào năm 1961, ông gọi nó là phương pháp bát đạo, vay mượn một thuật ngữ của Phật giáo. (Lưu ý: Dấu âm của số lạ là do một sự chọn lựa tùy tiện mà Gell-Mann đã thực hiện khi lần đầu tiên ông đưa ra thuật ngữ trên. Giá trị nêu ra ở đây chính xác, mặc dù nó có thể khiến một số độc giả cảm thấy bối rối).
Gell-Mann quả quyết rằng đối xứng SU(2) của bát đạo chỉ là sự bắt đầu của câu chuyện. Thật ra, nó là một phần của một đối xứng bậc cao hơn là SU(3), giống như lớp chính giữa của một cái bánh ba lớp. Những lớp ngoài cùng sẽ cho phép isospin lớn cỡ 3/2 và do đó có thể dung dưỡng cho một nhóm 10 hạt – decuplet – như thể hiện trong biểu đồ dưới đây. Một viên chức quân sự người Israel tên là Yuval Ne’eman (1925–2006), đã rời nước sang nghiên cứu vật lí ở London, cũng đề xuất sự đối xứng SU(3) trong khoảng thời gian trên.
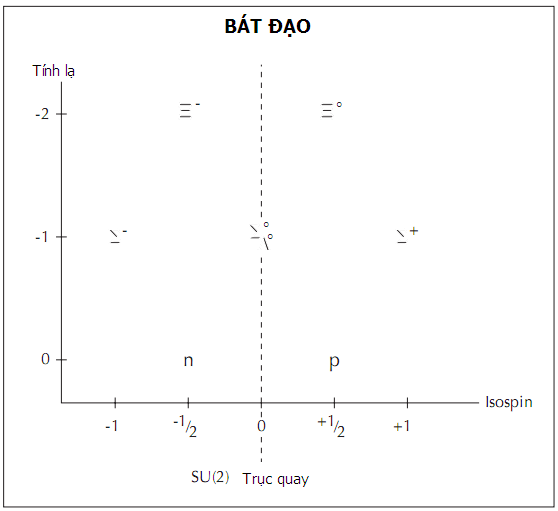
Murray Gell-Mann nhận ra một tính chất được bảo toàn mà ông gọi là tính lạ trong số những tính chất của “vườn bách thú” của các hạt hạ nguyên tử đã được khám phá. Với tính lạ trên một trục của đồ thị và isospin (một tính chất liên quan đến tương tác yếu) trên trục kia, ông đã nhận ra một đối xứng toán học gọi là SU(2) giữa những tập hợp gồm 8 hạt.
Các nhà vật lí đã thoáng trông thấy bốn hạt delta trong biểu đồ đó và xem chúng là “sự cộng hưởng” hay những trạng thái kích thích của proton và neutron. Sự tồn tại của chúng là cái khiến Gell-Mann và Ne’eman đi khảo sát SU(3) thay vì SU(2). Lí thuyết trên cung cấp cho các nhà vật lí máy gia tốc hạt một ý tưởng về nơi tìm kiếm những sự cộng hưởng khác, cái họ đã nhanh chóng tìm ra và đặt cho chúng những tên gọi mới bằng cách thêm dấu hoa thị cho các hạt sigma và xi trong biểu đồ SU(2). Chỉ có hạt omega trừ là vẫn hay lảng tránh vì khối lượng được cho là lớn của nó (lí thuyết của Gell-Mann tiên đoán nó nặng gấp 1800 lần proton), đòi hỏi những va chạm có năng lượng rất cao mới tạo ra được. Khi một đội nghiên cứu tại Phòng thí nghiệm quốc gia Brookhaven công bố đã khám phá ra nó vào năm 1964, với khối lượng của nó gần chính xác như giá trị Gell-Mann tiên đoán, thì rõ ràng đối xứng SU(3) là một phương thức hữu hiệu để mang trật tự đến với vườn bách thú hạt.
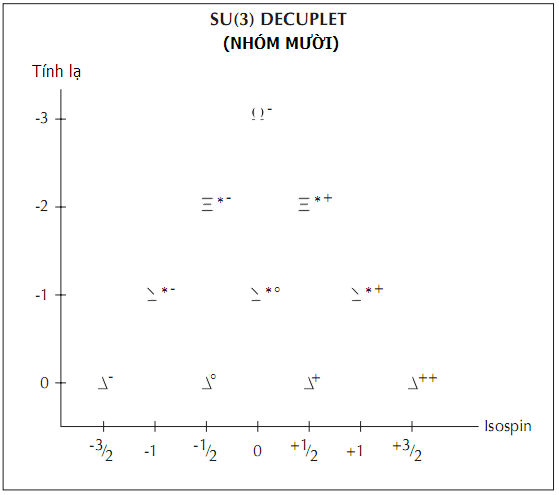
Gell-Mann và Yuval Ne’eman sớm nhận ra rằng đối xứng SU(2) đã thấy thật sự là một bộ phận của một mức độ đối xứng cao hơn gọi là SU(3). Tám hạt ấy giống như lớp chính giữa của một miếng bánh ba lớp, với các nhóm 10 hạt (decuplet) tạo nên những lớp bên ngoài.
Còn tiếp...
Xem lại Phần 38