Số hữu tỉ
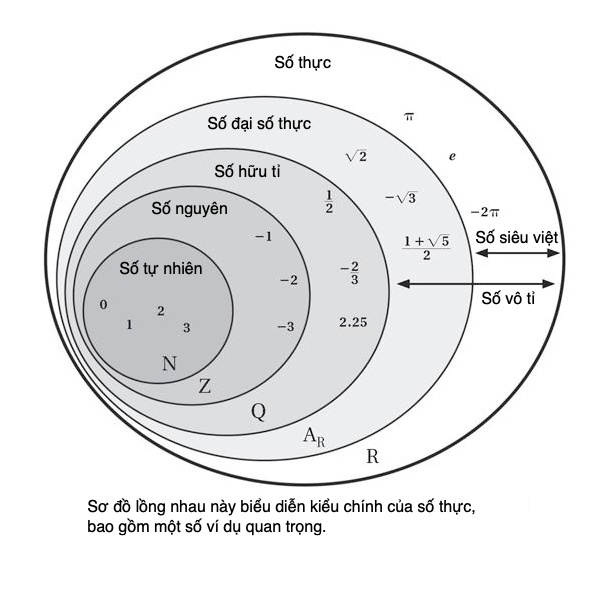
Số hữu tỉ là các số có thể biểu diễn bằng cách chia một số nguyên cho một số nguyên khác khác không. Như vậy, mọi số hữu tỉ đều có dạng phân số. Các số này được viết dưới dạng một con số, gọi là tử số, chia cho một số khác, gọi là mẫu số.
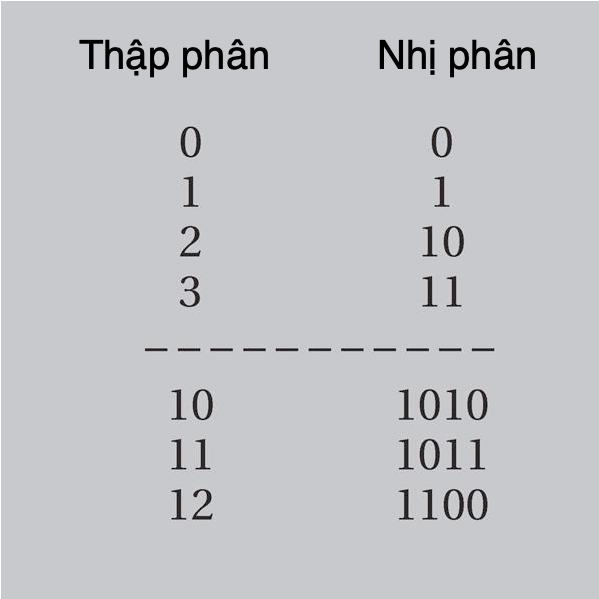
Khi biểu diễn ở dạng thập phân, số hữu tỉ hoặc là kết thúc sau một số lượng hữu hạn chữ số, hoặc là một hoặc một số chữ số lặp lại tuần hoàn. Chẳng hạn, 0,3333333… là một số hữu tỉ được biểu diễn ở dạng thập phân. Ở dạng phân số, con số bằng với nó là 1/3. Cũng đúng khi nói rằng mọi số thập phân có kết thúc hoặc tuần hoàn phải là số hữu tỉ, có thể biểu diễn được ở dạng phân số.
Vì có vô hạn số nguyên, nên chẳng có gì bất ngờ khi mà có vô số cách chia số này cho số kia, nhưng điều này không có nghĩa là số hữu tỉ có một “vô cực lớn hơn” của số nguyên.
Bình phương, căn bậc hai và lũy thừa
Bình phương của một con số x bất kì là tích của con số đó với chính nó, kí hiệu là x2. Tên gọi có xuất xứ từ thực tế diện tích của một hình vuông (với các cạnh bằng nhau) bằng độ dài một cạnh nhân với chính nó. Bình phương của một con số khác zero bất kì là dương, vì tích của hai số âm là dương và bình phương của zero là zero. Tương tự, một con số dương bất kì phải bằng bình phương của hai con số, x và –x. Đây là các căn bậc hai của nó.
Tổng quát hơn, nhân một con số x với chính nó n lần cho x lũy thừa n, viết là xn. Các số mũ có các quy tắc kết hợp riêng của chúng, phát sinh từ ý nghĩa của chúng\
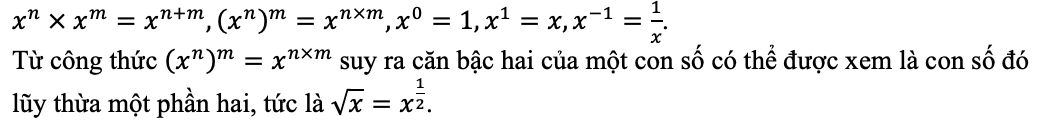
TOÁN HỌC CẤP TỐC
Paul Glendinning | Bản dịch của Thuvienvatly.com
Phần tiếp theo >>
