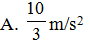📅 Ngày tải lên: 20/10/2024
📥 Tên file: 150 cau trac nghiem dao dong co nang cao-55468-thuvienvatly.doc (425KB)
🔑 Chủ đề: 150 cau trac nghiem dao dong co nang cao
150 câu trắc nghiệm Dao động cơ nâng cao
Cho các nhận định về quá trình dao động điều hòa của con lắc đơn.
1. Khi quả nặng ở vị trí biên, lực căng dây treo có độ lớn nhỏ hơn trọng lượng của vật.
2. Độ lớn của lực căng dây treo con lắc luôn lớn hơn trọng lượng vật.
3. Chu kỳ dao động của con lắc không phụ thuộc vào biên độ dao động của nó.
4. Khi góc hợp bởi phương dây treo con lắc và phương thẳng đứng giảm, tốc độ của quả nặng sẽ giảm.
Các nhận định sai là:
- (A) 2, 3.
- (B) 1, 2.
- (C) 2, 4.
- (D) 1, 4.
Tốc độ và li độ của một chất điểm dao động điều hoà có hệ thức, trong đó x tính bằng cm, v tính bằng cm/s. Tốc độ trung bình của chất điểm trong nửa chu kì là:
- (A) 8 cm/s.
- (B) 16 cm/s .
- (C) 32 cm/s .
- (D) 0 cm/s.
Một con lắc lò xo nhẹ có độ cứng k = 10N/m vật nhỏ có khối lượng m = 300g đặt trên sàn nằm ngang. Đặt lên vật m một vật nhỏ có khối lượng Dm = 100g, hệ số ma sát trượt giữa hai vật µ = 0,1. Cho hệ dao động điều hòa với biên độ 3cm, lấy g =10 m/s2. Khi hệ cách vị trí cân bằng 2cm, thì độ lớn lực ma sát tác dụng lên Dm bằng:
- (A) 0,4N
- (B) 0,15N
- (C) 0,05N
- (D) 0,03N
Một con lắc lò xo treo thẳng đứng, khi vật ở vị trí cân bằng lò xo giãn 6 cm. Kích thích cho vật dao động điều hòa thì thấy thời gian lò xo giãn trong một chu kì là 2T/3 (T là chu kì dao động của vật). Độ giãn lớn nhất của lò xo trong quá trình vật dao động là:
- (A) 24cm
- (B) 9cm.
- (C) 18cm
- (D) 12cm.
Cho 1 vật dao động điều hòa với biên độ A = 10cm, tần số f = 2Hz. Tốc độ trung bình mà vật có thể đi được trong thời gian 1/6 s là:
- (A) 60m/s
- (B) cm/s
- (C) cm/s
- (D) 30cm/s
Một vật dao động điều hòa với phương trình:
Quãng đường vật đi được từ thời điểm t1 = 1/10 (s) đến t2 = 6(s) là:
- (A) 337,5cm
- (B) 331,4cm
- (C) 333,8cm
- (D) 84,4cm
Hai con lắc đơn có chiều dài lần lượt là 81cm và 64cm được treo ở trần một căn phòng. Khi các vật nhỏ của hai con lắc đang ở vị trí cân bằng, đồng thời truyền cho chúng các vận tốc cùng hướng sao cho hai con lắc dao động điều hòa với cùng biên độ góc, trong hai mặt phẳng song song với nhau. Gọi Dt là khoảng thời gian ngắn nhất kể từ lúc truyền vận tốc đến lúc hai dây treo song song nhau. Giá trị Dt gần giá trị nào nhất sau đây?
- (A) 0,45s.
- (B) 7,20s.
- (C) 2,36s.
- (D) 8,12s.
Hai con lắc lò xo giống hệt nhau được treo vào hai điểm ở cùng độ cao, cách nhau 3cm. Kích thích cho hai con lắc dao động điều hòa theo phương thẳng đứng với phương trình lần lượt x1 = 3cosωt (cm) và x2 = 6cos(ωt+π/3) (cm). Trong quá trình dao động, khoảng cách lớn nhất giữa hai vật nhỏ của các con lắc bằng:
- (A) 8,5cm.
- (B) 5,2cm.
- (C) 6cm.
- (D) 9cm.
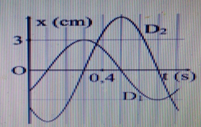
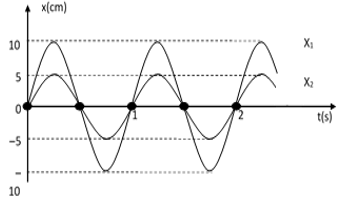
Dao động của một vật có khối lượng 200g là tổng hợp của hai dao động điều hòa cùng phương D1 và D2. Hình bên là đồ thị biểu diễn sự phụ thuộc của li độ của D1 và D2 theo thời gian. Mốc thế năng tại vị trí cân bằng của vật. Biết cơ năng của vật là 22,2mJ. Biên độ dao động của D2 có giá trị gần nhất với giá trị nào sau đây?
- (A) 5,7cm.
- (B) 4,8cm.
- (C) 5,4cm.
- (D) 5,1cm.
Con lắc lò xo treo thẳng đứng tại một nơi có gia tốc trọng trường là g. Tại vị trí cân bằng lò dãn Dl. Kéo quả nặng xuống theo phương thẳng đến vị trí cách vị trí cân bằng 2Dl rồi thả nhẹ để cho vật dao động điều hoà. Thời gian từ lúc thả đến lúc lò xo không bị biến dạng lần đầu tiên bằng:
- (A)
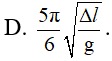
- (B)
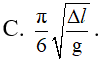
- (C)
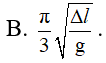
- (D)
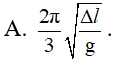
Hai vật dao động điều hòa dọc theo các trục song song với nhau. Phương trình dao động của các vật lần lượt là x1 = A1coswt (cm) và x2 = A2sinwt (cm). Biết . Tại thời điểm t, vật thứ nhất đi qua vị trí có li độ x1 = 3cm với vận tốc v1 = -18cm/s. Khi đó vật thứ hai có tốc độ bằng:
- (A) 8√3 cm/s.
- (B) 8cm/s.
- (C) 24cm/s.
- (D) 24 √3 cm/s.
Một lò xo nhẹ có độ cứng k, một đầu treo vào một điểm cố định, đầu dưới treo vật nặng 100g. Kéo vật nặng xuống dưới theo phương thẳng đứng rồi buông nhẹ. Vật dao động điều hòa theo phương trình x = 5cos4πt (cm), lấy g =10m/s2.và π2 = 10. Lực dùng để kéo vật trước khi dao động có độ lớn:
- (A) 3,2N
- (B) 6,4N
- (C) 1,6N.
- (D) 0,8N.
Con lắc lò xo gồm vật nặng m = 100g và lò xo nhẹ có độ cứng k = 100N/m. Tác dụng một ngoại lực cưỡng bức biến thiên điều hòa biên độ F0 và tần số f1 = 6Hz thì biên độ dao động A1. Nếu giữ nguyên biên độ F0 mà tăng tần số ngoại lực đến f2 = 7Hz thì biên độ dao động ổn định là A2. Lấy π2 = 10. So sánh A1 và A2:
- (A) Ch ưa đủ điều kiện để kết luận
- (B) A2>A1
- (C) A1>A2
- (D) A1=A2
Hai dao động điều hoà cùng phương, cùng tần số có phương trình và x2 = A2cos(t - π)cm. Dao động tổng hợp có phương trình x = 9cos(t+j) cm. Để biên độ A2 có giá trị cực đại thì A1 có giá trị:
- (A) 18 √3 cm
- (B) 15 √3 cm
- (C) 7cm
- (D) 9 √3 cm
Một con lắc lò xo treo thẳng đứng: lò xo nhẹ có độ cứng k, hai vật nặng M và m được nối với nhau bằng sợi dây khối lượng không đáng kể; gọi g là gia tốc trọng trường. Khi cắt nhanh sợi dây giữa m và M thì biên độ dao động của con lắc gồm lò xo và vật M sẽ là:
- (A)
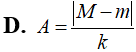
- (B)
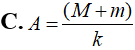
- (C)
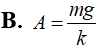
- (D)
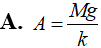
Một vật dao động điều hoà trên quỹ đạo dài 10cm với tần số f = 2Hz. Ở thời điểm ban đầu t = 0, vật chuyển động ngược chiều dương. Ở thời điểm t = 2s, vật có gia tốc a = 4√3m/s2. Lấy π2 ≈ 10. Phương trình dao động của vật là:
- (A) x = 10cos(4 π t + π /3)(cm).
- (B) x = 5cos(4 π t +5 π /6)(cm).
- (C) x = 2,5cos(4 π t +2 π /3)(cm).
- (D) x = 5cos(4 π t - π /3)(cm).
Một vật dao động điều hoà với tần số góc ω = 5rad/s. Lúc t = 0, vật đi qua vị trí có li độ là x = -2cm và có vận tốc 10(cm/s) hướng về phía vị trí biên gần nhất. Phương trình dao động của vật là:
- (A)
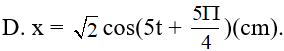
- (B)

- (C)
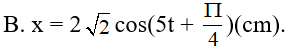
- (D)

Một con lắc lò xo nằm ngang dao động điều hoà xung quanh vị trí cân bằng với chu kỳ T = π/10 s. Đặt trục tọa độ Ox nằm ngang, gốc O tại vị trí cân bằng. Cho rằng lúc t = 0, vật ở vị trí có li độ x = -1 cm và được truyền vận tốc 20√3 cm/s theo chiều dương. Khi đó phương trình dao động của vật có dạng:
- (A) x = 2 sin (20t - π /3) cm.
- (B) x = 2 sin (20t - π /6) cm.
- (C) x = 2 cos (20t - π /6) cm.
- (D) x = 2 sin (20t + π /6) cm.
Một vật dao động điều hoà khi đi qua vị trí cân bằng theo chiều dương ở thời điểm ban đầu. Khi vật có li độ 3cm thì vận tốc của vật bằng 8π cm/s và khi vật có li độ bằng 4cm thì vận tốc của vật bằng 6π cm/s. Phương trình dao động của vật có dạng:
- (A) x = 5cos(2 π t + π ) (cm).
- (B) x = 10cos(2 π t- π /2 )(cm).
- (C) x = 5cos(2 π t + π /2 )(cm).
- (D) x = 5cos(2 π t- π /2 )(cm).
Một vật dao động có hệ thức giữa vận tốc và li độ là (x:cm; v:cm/s). Biết rằng lúc t = 0 vật đi qua vị trí x = A/2 theo chiều hướng về vị trí cân bằng. Lấy π2 = 10. Phương trình dao động của vật là:
- (A) x = 4cos(2 πt - π/3) (cm)
- (B) x = 8cos(2 πt + π/3) (cm)
- (C) x = 4cos(2 πt + π/3) (cm)
- (D) x = 4cos(4 πt + π/3) (cm)
Một con lắc dao động điều hòa theo phương trình (cm). Thời gian ngắn nhất kể từ lúc bắt đầu chuyển động đến thời điểm vật có vận tốc v = 20 cm/s là:
- (A) 1/12 (s)
- (B) 1/8 (s)
- (C) 5/12 (s)
- (D) 5/8 (s)
Một vật dao động điều hòa x = 10cos(10πt)(cm). Thời điểm vật đi qua vị trí li độ x = 5cm lần thứ 2009 theo chiều dương là:
- (A) 4018s.
- (B) 401,76s.
- (C) 410,8s.
- (D) 408,1s.
Một vật dao động điều hòa x = 10cos(10πt)(cm). Thời điểm vật đi qua vị trí N có li độ xN = 5cm lần thứ 2008 là:
- (A) 100,38s.
- (B) 2007,7s.
- (C) 200,8s.
- (D) 20,08s.
Một vật dao động điều hoà với . Thời điểm thứ 2012 vật qua vị trí có vận tốc v = - 8π cm/s là:
- (A) 2010 s.
- (B) 1004s .
- (C) 1005s .
- (D) 1005,5s .
Một vật dao động điều hòa với phương trình . Tốc độ trung bình của vật trong khoảng thời gian kể từ khi bắt đầu dao động là:
- (A) 79,33m/s.
- (B) 71,37m/s.
- (C) 77,37m/s.
- (D) 75,37m/s.
Vật dao động điều hòa với chu kì T. Thời gian ngắn nhất khi đi từ vị trí biên có li độ x = A đến vị trí x = -A/2, tốc độ trung bình là:
- (A) 4A/T
- (B) 9A/2T
- (C) 6A/T
- (D) 3A/2T
Một chất điểm dao động điều hòa theo phương trình (x tính bằng cm và t tính bằng giây). Trong một giây đầu tiên từ thời điểm t = 0, chất điểm đi qua vị trí có li độ x = +1cm:
- (A) 3 lần
- (B) 4 lần
- (C) 6 lần
- (D) 5 lần
Một vật dao động với phương trình , xác định quãng đường nhỏ nhất vật đi được trong 1/6(s):
- (A) 1,6cm .
- (B) 2 cm.
- (C) 2,1 cm.
- (D) 1,1 cm.
Một vật dao động với phương trình , xác định quãng đường lớn nhất vật đi được trong 1/4(s)?
- (A) 9,2cm
- (B) 7,5cm.
- (C) 8,4cm.
- (D) 6,7cm.
Một con lắc lò xo có vật nặng khối lượng m = 200g treo thẳng đứng dao động điều hoà. Chiều dài tự nhiên của lò xo là l0 = 30cm. Lấy g = 10m/s2. Khi lò xo có chiều dài l = 28cm thì vận tốc bằng không và lúc đó lực đàn hồi có độ lớn F = 2N. Năng lượng dao động của vật là:
- (A) 1,5J.
- (B) 0,08J.
- (C) 0,02J.
- (D) 0,1J.
Một con lắc lò xo dao động điều hòa theo phương thẳng đứng với chu kì và biên độ lần lượt là 0,4s và 8cm. Chọn trục x’x thẳng đứng, chiều dương hướng xuống, gốc tọa độ tại vị trí cân bằng, gốc thời gian (t = 0) khi vật qua vị trí cân bằng theo chiều dương. Lấy gia tốc rơi tự do g = 10 m/s2 và π2 = 10. Thời gian ngắn nhất kể từ khi t = 0 đến khi lực đàn hồi của lò xo có độ lớn cực tiểu là:
- (A) 4/15s
- (B) B . 7/30s
- (C) 3/10s
- (D) 1/30s
Một vật dao động điều hoà, khi vật có li độ x1 = 4cm thì vận tốc v = -40π√3 cm/s; khi vật có li độ x2 = 4√2 thì vận tốc v = 40π√2 cm/s. Động năng và thế năng biến thiên với chu kỳ:
- (A) 0,1s.
- (B) 0,8s.
- (C) 0,4s.
- (D) 0,2s.
Một vật dao động điều hoà quanh vị trí cân bằng theo phương trình x = 4cos(πt+π/2) (cm); t tính bằng giây. Biết rằng cứ sau những khoảng thời gian π/40 (s) thì động năng lại bằng nửa cơ năng. Tại những thời điểm nào thì vật có vận tốc bằng không?
- (A)
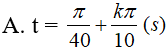
- (B)
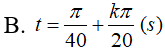
- (C)
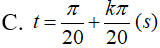
- (D)
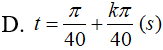
Một chất điểm dao động điều hòa trên trục Ox với biên độ 10cm, chu kì 2s. Mốc thế năng ở vị trí cân bằng. Tốc độ trung bình của chất điểm trong khoảng thời gian ngắn nhất khi chất điểm đi từ vị trí có động năng bằng 3 lần thế năng đến vị trí có động năng bằng 1/4 thế năng là:
- (A) 21,96 cm/s.
- (B) 14,64 cm/s.
- (C) 7,32 cm/s.
- (D) 26,12 cm/s.
Cho con lắc của đồng hồ quả lắc có α = 2.10-5K-1. Khi ở mặt đất có nhiệt độ 300C, đưa con lắc lên độ cao h = 640m so với mặt đất, ở đó nhiệt độ là 50C.Trong một ngày đêm đồng hồ chạy nhanh hay chậm bao nhiêu?
- (A) chậm 12,96s.
- (B) nhanh 3.10-4s.
- (C) chậm 3.10-4s.
- (D) nhanh 12,96s.
Con lắc của một đồng hồ coi như con lắc đơn có hệ số nở dài 2.10-4K-1. Đồng hồ chạy đúng khi ở mặt đất nhiệt độ 200C. Ở độ cao 1,6km đồng hồ vẫn chạy đúng. Cho bán kính Trái Đất là 6400km. Nhiệt độ trên cao là bao nhiêu?
- (A) 17,50C
- (B) 2,50C
- (C) 50C
- (D) 22,50C
Một con lắc đơn chu kỳ dao động 1,5s được treo vào trần một thang máy. Khi thang máy chuyển động thẳng đứng đi lên nhanh dần đều với gia tốc có độ lớn 2m/s2 thì chu kì dao động điều hòa của con lắc là:
- (A) 1,5s.
- (B) 1,68s.
- (C) 1,37s.
- (D) 1,42s.
Một con lắc đơn được treo vào trần một thang máy. Khi thang máy chuyển động thẳng đứng đi lên nhanh dần đều với gia tốc có độ lớn a thì chu kì dao động điều hòa của con lắc là 2,52s. Khi thang máy chuyển động thẳng đứng đi lên chậm dần đều với gia tốc cũng có độ lớn a thì chu kì dao động điều hòa của con lắc là 3,15s. Khi thang máy đứng yên thì chu kì dao động điều hòa của con lắc là:
- (A) 2,84s.
- (B) 2,61s.
- (C) 2,78s.
- (D) 2,96s.
Hai con lắc đơn có chiều dài lần lượt là 81cm và 64cm được treo ở trần một căn phòng, tại nơi có g = 10 m/s2. Khi các vật nhỏ của hai con lắc đang ở vị trí cân bằng, đồng thời truyền cho chúng các vận tốc cùng hướng sao cho hai con lắc dao động điều hòa với cùng biên độ góc, trong hai mặt phẳng song song với nhau. Gọi ∆t là khoảng thời gian ngắn nhất kể từ lúc truyền vận tốc đến lúc hai dây treo song song nhau. Giá trị ∆t gần giá trị nào nhất sau đây?
- (A) 8,12s.
- (B) B . 2,36s.
- (C) 7,20s.
- (D) 0,45s.
Gắn một vật có khối lượng m = 200g vào một lò xo có độ cứng k = 80N/m. Một đầu lò xo được giữ cố định. Kéo vật m khỏi vị trí cân bằng một đoạn 10cm dọc theo trục của lò xo rồi thả nhẹ cho vật dao động. Biết hệ số ma sát giữa vật m và mặt phẳng ngang là μ = 0,1. Lấy g = 10m/s2. Thời gian dao động của vật là:
- (A) 0,314s.
- (B) 3,14s.
- (C) 6,28s.
- (D) 2,00s.
Một con lắc đơn có chiều dài l = 64cm và khối lượng m = 100g. Kéo con lắc lệch khỏi vị trí cân bằng một góc 60 rồi thả nhẹ cho dao động. Sau 20 chu kì thì biên độ góc chỉ còn là 30. Lấy g = π2 = 10m/s2. Để con lắc dao động duy trì với biên độ góc 60 thì phải dùng bộ máy đồng hồ để bổ sung năng lượng có công suất trung bình là:
- (A) 0,77mW.
- (B) 0,082mW.
- (C) 17mW.
- (D) 0,077mW.
Cho một con lắc lò xo có độ cứng là k, khối lượng vật m = 1kg. Treo con lắc trên trần toa tầu ở ngay phía trên trục bánh xe. Chiều dài thanh ray là L = 12,5m. Tàu chạy với vận tốc 54km/h thì con lắc dao động mạnh nhất. Độ cứng của lò xo là:
- (A) 56,8N/m.
- (B) 100N/m.
- (C) 736N/m.
- (D) 73,6N/m.
Hai lò xo có độ cứng k1, k2 mắc nối tiếp, đầu trên mắc vào trần một toa xe lửa, đầu dưới mang vật m = 1kg. Khi xe lửa chuyển động với vận tốc 90km/h thì vật nặng dao động mạnh nhất. Biết chiều dài mỗi thanh ray là 12,5m, k1 = 200N/m, π2 = 10. Coi chuyển động của xe lửa là thẳng đều. Độ cứng k2 bằng:
- (A) 160N/m.
- (B) 40N/m.
- (C) 800N/m.
- (D) 80N/m.
Một con lắc lò xo gồm vật nhỏ khối lượng 0,02kg và lò xo có độ cứng 1N/m. Vật nhỏ được đặt trên giá đỡ cố định nằm ngang dọc theo trục lò xo. Hệ số ma sát trượt giữa giá đỡ và vật nhỏ là 0,1. Ban đầu giữ vật ở vị trí lò xo bị nén 10 cm rồi buông nhẹ để con lắc dao động tắt dần. Lấy g = 10m/s2. Tốc độ lớn nhất vật nhỏ đạt được trong quá trình dao động là:
- (A) 40 √3 c m/ s
- (B) 20 √6 c m/ s.
- (C) 10 √30 c m/ s.
- (D) 40 √2 c m/ s.
Một con lắc lò xo dao động điều hòa theo phương thẳng đứng. Trong quá trình dao động chiều dài của lò xo biến thiên từ 20cm đến 30cm. Trong một chu kì dao động thời gian lò xo nén bằng ½ thời gian lò xo giãn.Tính chiều dài tự nhiên của lò xo?
- (A) 22cm
- (B) 22,5cm
- (C) 25cm
- (D) 20cm
Cho đồ thị gia tốc có dạng hàm cos như hình vẽ. Biểu thức li độ vật dao động điều hòa là:
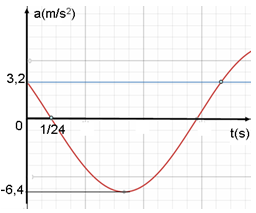
- (A)
cm
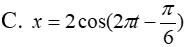
- (B)
cm
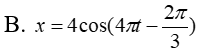
- (C)
cm
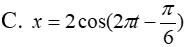
- (D)
cm
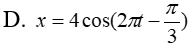
Một vật dao động điều hòa có T = 1(s). Biết tại thời điểm t vật có vận tốc là v = 4π cm/s thì sau đó nửa chu kỳ nữa vật có gia tốc a = 80√3 cm/s2. Tính tốc độ lớn nhất của vật (lấy p2 = 10).
- (A) 4 π cm/s
- (B) 12 π √3 cm/s
- (C) 8 π cm/s
- (D) 8 π √3 cm/s
Một vật dao động điều hòa có chu kì T. Biết tại thời điểm t vật có vận tốc là v = 4π cm/s thì sau đó 3/4 chu kỳ nữa vật có gia tốc a = 80cm/s2. Tính tốc độ lớn nhất của vật khi A = 4cm (lấy p2 = 10).
- (A) 4π cm/s
- (B) 12π √3 cm/s
- (C) 8π cm/s
- (D) 16π cm/s
Con lắc lò xo dao động điều hòa tại thời điểm t vật có a = 80 cm/s2 thì tốc độ vật là 4π√3 cm/s. Biết trong một chu kì vật có |a| ≥ 80 cm/s2 là 2T/3. Tìm A.
- (A) 6cm
- (B) 4cm
- (C) 2√3 cm
- (D) 2cm
Một dao động điều hòa mà 3 thời điểm liên tiếp gần nhau nhất t1, t2, t3 với t3 – t1 = 3(t3 – t2) = 0,1π (s), vật có cùng độ lớn gia tốc 1 m/s2 cụ thể là a1 = - a2 = -a3 = 1m/s2). Gia tốc cực đại vật gần giá trị nào sau đây nhất?
- (A) 1,16 m/s2
- (B) 2,1 m/s2
- (C) 2 √2 m/s2
- (D) 3,8 m/s2.
Một vật dao động điều hòa có phương trình . Lần thứ 2 vật thỏa mãn hệ thức kể từ thời điểm ban đầu ứng với thời điểm nào sau đây?
- (A) T/24
- (B) 7T/12
- (C) 7T/24
- (D) 11T/12
Hai điểm sáng dao động điều hòa trên cùng 1 trục, cùng vị trí cân bằng và dao động cùng ω nhưng biên độ lần lượt A1; A2. Biết A1 + A2 = 8cm và tại mọi thời điểm chúng có li độ và vận tốc thỏa mãn x1v2 + x2v1 = 8 cm2/s. Giá trị nhỏ nhất của ω là:
- (A) 0,5(rad/s)
- (B) 2(rad/s)
- (C) 1(rad/s)
- (D) 4(rad/s)
Con lắc của một đồng hồ coi như con lắc đơn. Đồng hồ chạy đúng khi ở mặt đất. Ở độ cao 3,2km nếu muốn đồng hồ vẫn chạy đúng thì phải thay đổi chiều dài con lắc như thế nào? Cho bán kính Trái Đất là 6400km.
- (A) Tăng 0,1%.
- (B) Tăng 0,2%.
- (C) Giảm 0,2%.
- (D) Giảm 0,1%.
Một con lắc lò xo gồm lò xo độ cứng k = 50N/m, vật nặng có khối lượng m = 200g được treo thẳng đứng, dao động giữa hai điểm cao nhất và thấp nhất cách nhau 6cm. Tính tỉ số lực đàn hồi cực đại và cực tiểu của lò xo.
- (A) 5
- (B) 6
- (C) 7
- (D) 10
Một con lắc đơn có khối lượng vật nặng là m, chiều dài dây treo là 1m, dao động điều hoà dưới tác dụng của ngoại lực N. Lấy g = π2 = 10m/s2. Nếu tần số f của ngoại lực thay đổi từ 1Hz đến 2Hz thì biên độ dao động của con lắc sẽ:
- (A) không thay đổi.
- (B) giảm.
- (C) tăng.
- (D) tăng rồi giảm.
Khi gắn vật có khối lượng m1 vào một lò xo có khối lượng không đáng kể, nó dao động với chu kì T1 = 2s. Khi gắn vật có khối lượng m2 vào một lò xo trên nó dao động với chu kì T1 = 8s. Chọn đáp án sai.
- (A)
Khi gắn vật nặng có khối lượng thì chu kỳ dao động là 4s.
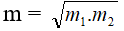
- (B) Khi vật nặng có khối lượng m = 9m1+m2 thì chu kỳ là 10s.
- (C) Khi vật nặng có khối lượng m = m1+m2 thì chu kỳ là 9s.
- (D) Khi vật nặng có khối lượng m = m2- 7m1 thì chu kỳ dao động là 6s.
Hai dao động điều hòa cùng phương, cùng tần số, dao động 1 có biên độ A1=10cm, pha ban đầu p/6 và dao động 2 có biên độ A2, pha ban đầu -p/2. Biên độ A2 thay đổi được. Biên độ dao động tổng hợp A có giá trị nhỏ nhất là bao nhiêu?
- (A) A = 2 √3 (cm)
- (B) A = 5√3 (cm)
- (C) A = 2,5√3 (cm)
- (D) A = √3 (cm)
Một vật có khối lượng không đổi thực hiện đồng thời hai dao động điều hòa x1 = 10 cos(ωt + φ1) và x2 = A2 cos(ωt – π/2), phương trình dao động tổng hợp của vật là x = A cos(ωt – π/3). Để vật dao động với cơ năng cực đại thì A2 bằng bao nhiêu?
- (A) 10 √3 cm
- (B) 5 √3 cm
- (C) 10 cm
- (D) 5 cm
Một chất điểm dao động điều hòa có ly độ phụ thuộc thời gian theo hàm cosin như mô tả trên đồ thị. Phương trình dao động của chất điểm là:
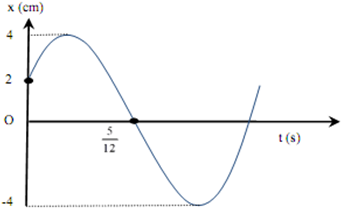
- (A)
- (B)
- (C)
- (D)
Một chất điểm dao động điều hòa hàm cosin có vận tốc biểu diễn như đồ thị. Lấy π2=10. Phương trình dao động của vật là:
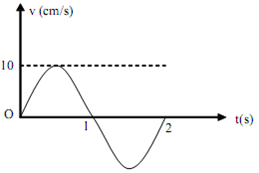
- (A) x = 10 π cos( π t + π )cm
- (B) x = π cos( π t)cm
- (C) x = 10 π cos( π t)cm
- (D) x = π cos( π t + π )cm
Một lò xo có độ cứng k = 20N/m treo thẳng đứng. Treo vào đầu dưới lò xo một vật có khối lượng m = 200g. Từ vị trí cân bằng nâng vật lên 5cm rồi buông nhẹ ra. Lấy g = 10m/s2. Trong quá trình vật dao động, giá trị cực tiểu và cực đại của lực đàn hồi của lò xo là:
- (A) 2N và 5N.
- (B) 2N và 3N.
- (C) 1N và 5N.
- (D) 1N và 3N.
Một chất điểm có khối lượng m dao động điều hoà xung quanh vị cân bằng với biên độ A. Gọi vmax , amax, WDmax lần lượt là độ lớn vận tốc cực đại, gia tốc cực đại và động năng cực đại của chất điểm. Tại thời điểm t chất điểm có ly độ x và vận tốc là v. Công thức nào sau đây là không dùng để tính chu kì dao động điều hoà của chất điểm?
- (A)
- (B)
- (C)
- (D)
Một con lắc đơn có chiều dài dây treo 50cm và vật nhỏ có khối lượng 0,01kg mang điện tích q = +5.10-6C được coi là điện tích điểm. Con lắc dao động điều hoà trong điện trường đều mà vectơ cường độ điện trường có độ lớn E = 104V/m và hướng thẳng đứng xuống dưới. Lấy g = 10 m/s2, π = 3,14. Chu kì dao động điều hoà của con lắc là:
- (A) 1,40s
- (B) 1,15s
- (C) 0,58s
- (D) 1,99s
Một con lắc đơn gồm một sợi dây có chiều dài 1m và quả nặng có khối lượng m = 100g, mang điện tích q = 2.10-5C . Treo con lắc vào vùng không gian có điện trường đều theo phương nằm ngang với cường độ 4.104V/m và gia tốc trọng trường g = π2 = 10m/s2. Chu kì dao động của con lắc là:
- (A) 1,36s.
- (B) 1,76s.
- (C) 2,56s.
- (D) 2,47s.
Treo con lắc đơn vào trần một ôtô tại nơi có gia tốc trọng trường g = 9,8m/s2. Khi ôtô đứng yên thì chu kì dao động điều hòa của con lắc là 2s. Nếu ôtô chuyển động thẳng nhanh dần đều trên đường nằm ngang với giá tốc 2m/s2 thì chu kì dao động điều hòa của con lắc xấp xỉ bằng:
- (A) 1,82s.
- (B) 2,02s.
- (C) 1,98s.
- (D) 2,00s.
Vật dao động điều hòa với phương trình x = 6cos(ωt – π/2) (cm). Sau thời gian t1 = 0,5s kể từ thời điểm ban đầu vật đi được quãng đường 3 cm. Sau khoảng thời gian t2 = 20,5s kể từ thời điểm ban đầu vật đi được quãng đường:
- (A) 123cm.
- (B) 75cm.
- (C) 72cm.
- (D) 81cm.
Hai con lắc đơn giống nhau có chu kì To. Nếu tích điện cho hai vật nặng các giá trị lần lượt là q1 và q2, sau đó đặt hai con lắc trong một điện trường đều E hướng thẳng đứng xuống dưới thì chu kì dao động của hai con lắc lần lượt là T1 = 5To và Tỉ số q1/q2 bằng:
- (A) -1
- (B) 7
- (C) -2
- (D) 0,5
Cho một con lắc lò xo treo thẳng đứng. Một học sinh tiến hành hai lần kích thích dao động. Lần thứ nhất, nâng vật lên rồi thả nhẹ thì thời gian ngắn nhất vật đến vị trí lực đàn hồi cực tiểu là x. Lần thứ hai, đưa vật về vị trí lò xo không biến dạng rồi thả nhẹ thì thời gian ngắn nhất đến lực phục hồi đổi chiều là y, tỉ số . Tỉ số gia tốc vật và gia tốc trọng trường ngay khi thả lần thứ nhất là:
- (A) 3
- (B) 3/2
- (C) 1/5
- (D) 2
Một con lắc đơn có chiều dài dây treo bằng 1m, khối lượng quả nặng là m dao động cưỡng bức dưới tác dụng của ngoại lực F = Focos(2πft + π/2). Lấy g = π2 = 10m/s2. Nếu tần số của ngoại lực thay đổi từ 0,1Hz đến 2Hz thì biên độ dao động của con lắc:
- (A) không thay đổi.
- (B) tăng rồi giảm.
- (C) giảm rồi tăng.
- (D) luôn tăng.
Một vật dao động điều hòa với biên độ 13cm, t = 0 tại biên dương. Sau khoảng thời gian t (kể từ lúc ban đầu chuyển động) thì vật cách vị trí cân bằng O một đoạn 12cm. Sau khoảng thời gian 2t (kể từ t = 0) vật cách O một đoạn bằng x. Giá trị x gần giá trị nào nhất sau đây?
- (A) 9,35cm
- (B) 8,75cm
- (C) 6,15cm
- (D) 7,75cm
Thời gian mà một vật dao động điều hòa với chu kì T đi được một quãng đường đúng bằng biên độ không thể nhận giá trị nào sau đây?
- (A) T/8
- (B) T/3
- (C) T/4
- (D) T/6
Chiều dài của con lắc lò xo treo thẳng đứng dao động điều hòa biến đổi từ 30cm tới 40cm. Độ cứng của lò xo là k = 100N/m. Khi lò xo có chiều dài 38cm thì lực đàn hồi tác dụng vào vật là 10N. Độ biến dạng lớn nhất của lò xo là:
- (A) 10cm.
- (B) 12cm.
- (C) 7cm.
- (D) 5cm.
Một con lắc lò xo gồm một lò xo nhẹ có độ cứng k và vật nhỏ khối lượng 1kg. Con lắc dao động điều hòa theo phương ngang với chu kì T. Biết ở thời điểm t vật có li độ 5cm, ở thời điểm vật có tốc độ 50cm/s. Độ cứng k bằng:
- (A) 150N/m.
- (B) 100N/m.
- (C) 200N/m.
- (D) 50N/m.
Cho hai con lắc lò xo giống hệt nhau. Kích thích cho hai con lắc dao động điều hòa với biên độ lần lượt là 2A và A dao động cùng pha. Chọn gốc thế năng tại vị trí cân bằng của hai con lắc. Khi động năng của con lắc thứ nhất là 0,6J thì thế năng của con lắc thứ hai là 0,05J. Khi thế năng của con lắc thứ nhất là 0,4J thì động năng của con lắc thứ hai là:
- (A) 0,4J.
- (B) 0,1J.
- (C) 0,2J.
- (D) 0,6J.
Có hai con lắc lò xo giống hệt nhau dao động điều hòa trên mặt phẳng nằm ngang dọc theo hai đường thẳng song song cạnh nhau và song song với trục Ox. Biên độ của con lắc một là A1 = 4cm, của con lắc hai là A2 = 4√3 cm, con lắc hai dao động sớm pha hơn con lắc một. Trong quá trình dao động khoảng cách lớn nhất giữa hai vật dọc theo trục Ox là 4cm. Khi động năng con lắc một cực đại là W thì động năng con lắc hai là:
- (A) 3/4 W.
- (B) 2/3 W.
- (C) 9/4 W.
- (D) 5/3 W.
Một chất điểm dao động điều hòa không ma sát. Khi vừa qua khỏi vị trí cân bằng một đoạn S, động năng của chất điểm là 1,8J. Đi tiếp một đoạn S nữa thì động năng chỉ còn 1,5J và nếu đi thêm một đoạn S nữa thì động năng bây giờ là:
- (A) 0,9J.
- (B) 1,0J.
- (C) 0,8J.
- (D) 1,2J.
Một vật dao động điều hòa với phương trình (t tính bằng giây). Số lần vật đi qua vị trí có động năng bằng 8 lần thế năng từ thời điểm t1 = 1/6 s đến thời điểm t2 = 13/3 s là:
- (A) 8 lần.
- (B) 9 lần.
- (C) 10 lần.
- (D) 11 lần.
Lần lượt tác dụng các lực F1 = Focos(12πt) (N); F2 =Focos(14πt) (N); F3 = Focos(16πt) (N); = Focos(18πt) (N) vào con lắc lò xo có độ cứng k = 100N/m; khối lượng m = 100g. Lực làm cho con lắc dao động với biên độ nhỏ nhất là:
- (A) F1 = Focos(12πt) (N).
- (B) F2 =Focos(14πt) (N).
- (C) F3 = Focos(16πt) (N).
- (D) F1 = Focos(18πt) (N).
Hai chất điểm M1, M2 cùng dao động điều hòa trên trục Ox xung quanh gốc O với cùng tần số f, biên độ dao động của M1, M2 tương ứng là 6cm, 8cm và dao động của M2 sớm pha hơn M1 một góc π/2 rad. Khi khoảng cách giữa hai vật là 10cm thì M1 và M2 cách gốc tọa độ lần lượt là:
- (A) 6,40cm và 3,60cm.
- (B) 5,72cm và 4,28cm.
- (C) 4,28cm và 5,72cm.
- (D) 3,60cm và 6,40cm.
Trên mặt bàn nhẵn có một con lắc lò xo đang nằm ngang với quả cầu có khối lượng m = 100g; Hai chất điểm M1, M2 cùng dao động điều hòa trên trục Ox xung quanh gốc O với cùng tần số f. Quả cầu nằm cân bằng. Tác dụng lên quả cầu một lực có hướng nằm ngang và có độ lớn bằng 20N trong thời gian 3. 10-3s, sau đó quả cầu dao động điều hòa. Biên độ dao động của quả cầu xấp xỉ bằng:
- (A) 4,8cm.
- (B) 0,6cm.
- (C) 6,7cm.
- (D) 10cm.
Một con lắc lò xo có tần số riêng ω = 25 rad/s, rơi tự do mà trục lò xo thẳng đứng, vật năng bên dưới. Ngay khi con lắc có vận tốc 42 cm/s thì đầu trên lò xo bị giữ lại. Tính vận tốc cực đại của con lắc.
- (A) 60cm/s.
- (B) 58cm/s.
- (C) 73cm/s.
- (D) 67cm/s.
Ba vật A, B, C có khối lượng lần lượt là 400g, 500g và 700g được móc nối tiếp vào một lò xo, B nối với A và C nối với B. Khi bỏ C đi thì hệ dao động với chu kì 3s. Chu kì dao động của hệ khi chưa bỏ C và khi bỏ cả C và B lần lượt là:
- (A) 2s và 4s.
- (B) 2s và 6s.
- (C) 4s và 2s.
- (D) 6s và 1s.
Con lắc lò xo gồm vật nhỏ có khối lượng m = 1kg và lò xo nhẹ có độ cứng k = 100N/m được treo thẳng đứng vào một điểm cố định. Vật được đặt trên một giá đỡ D. Ban đầu giá đỡ D đứng yên và lò xo giãn 1cm. Cho D chuyển động nhanh dần đều thẳng đứng xuống dưới với gia tốc a = 1m/s2. Bỏ qua mọi ma sát và lực cản, lấy g = 10m/s2. Sau khi rời khỏi giá đỡ, vật m dao động điều hòa với biên độ xấp xỉ bằng:
- (A) 6,08cm.
- (B) 9,80cm.
- (C) 5,74cm.
- (D) Đáp án khác
Một vật dao động theo phương trình (cm;s). Kể từ lúc t = 0 đến lúc vật qua li độ -10cm theo chiều âm lần thứ 2013 thì lực phục hồi sinh công âm trong khoảng thời gian:
- (A) 2013,08s.
- (B) 1027,88s.
- (C) 1207,4s.
- (D) 2415,8s.
Một vật có khối lượng m = 500g rơi tự do không vận tốc đầu từ độ cao h = 40cm lên một đĩa cân (h so với mặt đĩa cân), bên dưới đĩa cân có gắn một lò xo thẳng đứng có độ cứng k = 40N/m. Khi chạm vào đĩa vật gắn chặt vào đĩa (va chạm mềm) và dao động điều hòa. Bỏ qua khối lượng đĩa và mọi ma sát. Năng lượng dao động của vật là:
- (A) 3,2135J.
- (B) 5,3125J.
- (C) 2,5312J.
- (D) 2,3125J.
Trong khoảng thời gian từ τ đến 2τ, vận tốc của một vật dao động điều hòa tăng từ 0,6vmax đến vmax rồi giảm về 0,8vmax. Tại thời điểm t = 0, li độ của vật là:
- (A)
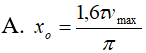
- (B)
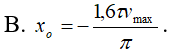
- (C)
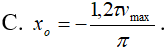
- (D)
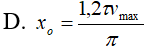
Một vật nhỏ có khối lượng M = 0,9kg gắn trên một lò xo nhẹ thẳng đứng có độ cứng 25N/m, đầu dưới của lò xo cố định. Một vật nhỏ có khối lượng m = 0,1kg chuyển động theo phương thẳng đứng với tốc độ 0,2√2 m/s đến va chạm mềm với M. Sau va chạm, hai vật dính vào nhau và cùng dao động điều hòa theo phương thẳng đứng trùng với trục của lò xo. Lấy gia tốc trọng trường g = 10m/s2. Biên độ dao động là:
- (A) 4,5 cm.
- (B) 4 cm.
- (C) 4 √2 cm.
- (D) 4 √3 cm.
Con lắc lò xo gồm vật nặng M = 300g, lò xo có độ cứng k = 200N/m, lồng vào một trục thẳng đứng như hình vẽ. Khi M đang ở vị trí cân bằng thì vật m = 200g từ độ cao h = 3,75m so với M rơi tự do, va chạm mềm với M, coi ma sát là không đáng kể, lấy g = 10m/s2. Sau va chạm hai vật cùng dao động điều hòa, chọn gốc tọa độ tại vị trí cân bằng của hệ, chiều dương như hình vẽ, gốc thời gian t = 0 là lúc va chạm. Phương trình dao động của hệ hai vật là:
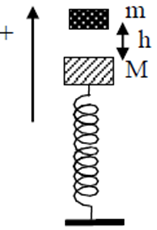
- (A) x = 1,08cos(20t + 0,378) cm.
- (B) x = 2,13cos(20t + 1,093) cm.
- (C) x = 1,57cos(20t + 0,155) cm.
- (D) Đáp án khác
Hai vật A, B dán liền nhau mB = 2mA = 200g, treo vào một lò xo có độ cứng k = 50N/m, có chiều dài tự nhiên 30cm. Nâng vật theo phương thẳng đứng đến vị trí lò xo có chiều dài tự nhiên rồi buông nhẹ. Vật dao động điều hòa đến vị trí lực đàn hồi của lò xo có độ lớn lớn nhất, vật B bị tách ra. Tính chiều dài nhắn nhất của lò xo.
- (A) 26cm
- (B) 24cm
- (C) 30cm
- (D) 22cm
Một con lắc lò xo đặt nằm ngang gồm vật M có khối lượng 400g và lò xo có hệ số cứng 40N/m đang dao động điều hòa xung quanh vị trí cân bằng với biên độ 5cm. Khi M qua vị trí cân bằng người ta thả nhẹ vật m có khối lượng 100g lên M (m đính chặt ngay vào M), sau đó hệ m và M dao động với biên độ:
- (A) 2 √5 cm.
- (B) 4,25cm.
- (C) 3 √2 cm.
- (D) 2 √2 cm.
Một vật có khối lượng m1 = 1,25kg mắc vào lò xo nhẹ có độ cứng k = 200N/m, đầu kia của lò xo gắn chặt vào tường. Vật và lò xo đặt trên mặt phẳng nằm ngang có ma sát không đáng kể. Đặt vật thứ hai có khối lượng m2 = 3,75kg sát với vật thứ nhất rồi đẩy chậm cả hai vật cho lò xo nén lại 8cm. Khi thả nhẹ chúng ra, lò xo đẩy hai vật chuyển động về một phía. Lấy π2 = 10. Khi lò xo giãn cực đại lần đầu tiên thì hai vật cách xa nhau một đoạn là:
- (A) (4π – 4) cm.
- (B) (2π – 4) cm.
- (C) 16cm.
- (D) (4π – 8) cm.
Một con lắc lò xo gồm lò xo có độ cứng k = 100N/m và vật nặng có khối lượng m = 5/9 kg đang dao động điều hòa theo phương ngang với biên độ 2cm trên mặt phẳng nhẵn nằm ngang. Tại thời điểm m qua vị trí động năng bằng thế năng, một vật nhỏ có khối lượng mo = 0,5m rơi thẳng đứng và dính chặt vào m. Khi qua vị trí cân bằng hệ (m + mo) có tốc độ bằng:
- (A) 20cm/s.
- (B) 30 √3 cm/s.
- (C) 25cm/s.
- (D) 5 √12 cm/s.
Một con lắc lò xo dao động tắt dần trên mặt phẳng nằm ngang với các thông số như sau: m = 0,1kg; vmax = 1m/s; μ = 0,05. Tính độ lớn vận tốc của vật khi vật đi được 10cm.
- (A) 0,95 cm/s.
- (B) 0,3 cm/s.
- (C) 0,95 m/s.
- (D) 0,3m/s.
Một con lắc lò xo gồm vật m1 (mỏng phẳng) có khối lượng 2kg và lò xo có độ cứng k = 100N/m đang dao động điều hòa trên mặt phẳng nằm ngang không ma sát với biên độ 5cm. Khi vật m1 đến vị trí biên người ta đặt nhẹ lên nó một vật có khối lượng m2. Cho hệ số ma sát giữa vật m1 và vật m2 là 0,2; lấy g = 10m/s2. Giá trị của m2 để nó không bị trượt trên m1 là:
- (A) m 2 ≥ 0,5kg
- (B) m 2 ≤ 0,5kg
- (C) m 2 ≥ 0,4kg
- (D) m 2 ≤ 0,4kg
Một con lắc lò xo gồm vật nhỏ khối lượng 0,2kg và lò xo có độ cứng 20N/m. Vật nhỏ được đặt trên giá cố định nằm ngang dọc theo trục nằm ngang. Hệ số ma sát trượt giữa giá đỡ và vật nhỏ là 0,01. Từ vị trí lò xo không biến dạng truyền cho vật vận tốc đầu 1m/s thì thấy con lắc dao động tắt dần trong giới hạn đàn hồi của lò xo. Độ lớn của lực đàn hồi cực đại của lò xo trong quá trình dao động là:
- (A) 19,8N
- (B) 1,5 N
- (C) 2,2N
- (D) 1,98N
Một con lắc lò xo thẳng đứng gồm lò xo nhẹ có độ cứng k = 100N/m, một đầu cố định, một đầu gắn vật nặng khối lượng m = 0,5kg. Ban đầu kéo vật theo phương thẳng đứng khỏi vị trí cân bằng 5cm rồi buông nhẹ cho dao động. Trong quá trình dao động vật luôn chịu tác dụng của lực cản có độ lớn bằng 1/100 trọng lực tác dụng lên vật. Coi biên độ của vật giảm đều trong từng chu kì, lấy g = 10m/s2. Số lần vật qua vị trí cân bằng kể từ khi thả vật tới khi dừng hẳn là:
- (A) 25
- (B) 50
- (C) 75
- (D) 100
Con lắc lò xo nằm ngang gồm lò xo có độ cứng k = 20N/m và vật nặng m = 100g. Từ vị trí cân bằng kéo vật ra một đoạn 6cm rồi truyền cho vật vận tốc 10√14 cm/s hướng về vị trí cân bằng. Biết rằng hệ số ma sát giữa vật và mặt phẳng ngang là 0,4, lấy g = 10m/s2. Tốc độ cực đại của vật sau khi truyền vận tốc bằng:
- (A) 20 √22 cm/s.
- (B) 80 √2 cm/s.
- (C) 20 √10 cm/s.
- (D) 40 √6 cm/s.
Một con lắc lò xo treo thẳng đứng, lò xo có khối lượng không đáng kể, có k = 100N/m, treo quả nặng có khối lượng 100g. Chọn gốc tọa độ tại vị trí cân bằng, chiều dương của trục tọa độ Ox thẳng đứng xuống dưới. Kích thích cho vật dao động điều hòa theo phương thẳng đứng với biên độ 3cm. Lấy g = 10m/s2. Công của lực đàn hồi khi vật di chuyển theo chiều dương từ vị trí có tọa độ x1 = 1cm đến vị trí x2 = 3cm.
- (A) -4J
- (B) -0,04J
- (C) -0,06J
- (D) 6J
Một con lắc lò xo gồm một vật nhỏ khối lượng 100g và lò xo nhẹ có độ cứng 0,01N/cm. Ban đầu giữ vật ở vị trí lò xo giãn 10cm rồi buông nhẹ cho vật dao động. Trong quá trình dao động lực cản tác dụng lên vật có độ lớn không đổi 10-3N. Lấy π2 = 10. Sau 21,4s dao động, tốc độ lớn nhất của vật chỉ có thể là:
- (A) 58π mm/s
- (B) 57π mm/s
- (C) 56π mm/s
- (D) 54π mm/s
Một con lắc đơn gồm dây treo có chiều dài l =1m, vật nặng có khối lượng 100g, dao động nhỏ tại nơi có gia tốc trọng trường g = 10m/s2. Cho con lắc dao động với biên độ góc 0,2 rad trong môi trường có lực cản không đổi thì nó chỉ dao động được 150s rồi dừng hẳn. Người ta duy trì dao động bằng cách dùng hệ thống lên dây cót, biết rằng 70% năng lượng dùng để thắng lực ma sát do hệ thống các bánh răng. Lấy π2 = 10. Công cần thiết để lên dây cót để duy trì con lắc dao động trong hai tuần với biên độ 0,2 rad là:
- (A) 537,6J
- (B) 161,28J
- (C) 522,25J
- (D) 230,4J
Một con lắc lò xo nằm ngang gồm lò xo nhẹ có độ cứng k = 40N/m, một đầu gắn vào giá cố định, đầu còn lại gắn vào vật nhỏ có khối lượng m = 100g. Ban đầu giữ vật sao cho lò xo nén 4,8cm rồi thả nhẹ. Hệ số ma sát trượt và ma sát nghỉ giữa vật và mặt bàn đều bằng nhau và bằng 0,2. Lấy g = 10m/s2. Tính quãng đường cực đại vật đi được cho tới khi dừng hẳn.
- (A) 23cm
- (B) 64cm
- (C) 32cm
- (D) 36cm
Một con lắc lò xo nằm ngang trên mặt bàn, lò xo có độ cứng k = 20N/m, vật nặng có khối lượng m = 400g. Đưa vật nặng sang trái đến vị trí lò xo nén 4cm rồi thả nhẹ cho vật dao động. Biết rằng hệ số ma sát trượt và hệ số ma sát nghỉ coi bằng nhau. Muốn cho vật dừng lại ở bên phải vị trí lò xo không biến dạng, trước khi nó đi qua vị trí này lần 2 thì hệ số ma sát μ giữa vật với mặt bàn có phạm vi biến thiên là:
- (A) μ ≥ 0,1
- (B) μ ≤ 0,05
- (C) 0,05 ≤ μ ≤ 0,1
- (D) μ ≤ 0,05 và μ ≥ 0,1
Một con lắc lò xo dao động trên mặt phẳng nằm ngang có hệ số ma sát μ = 0,01. Lò xo có độ cứng k = 100N/m, vật có khối lượng m = 100g, lấy g = 10m/s2. Lúc đầu đưa vật đi tới vị trí cách vị trí cân bằng 4cm rồi buông nhẹ để vật dao động tắt dần. Tốc độ trung bình kể từ lúc vật bắt đầu dao động đến lúc vật dừng lại là:
- (A) 0,425m/s
- (B) 0,525m/s
- (C) 0,225m/s
- (D) 4,026m/s
Một lò xo nhẹ, dài tự nhiên 20cm, giãn ra 1cm dưới tác dụng của lực kéo 0,1N. Đầu trên của lò xo gắn vào điểm O, đầu dưới treo vật nặng 10g. Hệ đang đứng yên. Quay lò xo quanh trục thẳng đứng qua O với một tốc độ không đổi thì thấy trục lò xo làm với phương thẳng đứng góc 60o. Lấy g = 10m/s2. Chiều dài của lò xo và tốc độ quay xấp xỉ bằng:
- (A) 20cm; 15 vòng/s.
- (B) 22cm; 15 vòng/s.
- (C) 20cm; 1,5 vòng/s.
- (D) 22cm; 1,5 vòng/s.
Hai vật dao động điều hòa cùng pha ban đầu, cùng phương và cùng thời điểm với các tần số góc lần lượt là ω1 = π/6 rad/s; ω2 = π/3 rad/s. Chọn gốc thời gian lúc hai vật đi qua vị trí cân bằng theo chiều dương. Thời gian ngắn nhất mà hai vật gặp nhau là:
- (A) 1s.
- (B) 4s.
- (C) 2s.
- (D) 8s.
Một vật thực hiện đồng thời hai dao động điều hòa x1 = A1cos(ωt) cm; x2 = 2,5√3cos(ωt + φ2) và người ta thu được biên độ mạch dao động là 2,5cm. Biết A1 đạt cực đại, hãy xác định φ2?
- (A) không xác định được.
- (B) π/6 rad
- (C) 2 π/3 rad
- (D) 5 π/6 rad
Cho hai vật dao động điều hòa cùng phương x1 = 2cos(4t +φ1); x2 = 2cos(4t + φ2) với 0 ≤ φ1 – φ2 ≤ π/2 (rad). Biết phương trình dao động tổng hợp là (cm) Giá trị của φ1 là:
- (A) π/6
- (B) - π/6
- (C) π/2
- (D) - π/2
Một con lắc lò xo có khối lượng m dao động cưỡng bức ổn định dưới tác dụng của ngoại lực biến thiên điều hòa với tần số f. Khi f = f1 thì vật có biên độ là A1, khi f = f2 (f1 < f2 < 2f1) thì vật có biên độ là A2, biết A1 = A2. Độ cứng của lò xo là:
- (A)
- (B)
- (C)
- (D)
Dao động của một chất điểm là tổng hợp của hai dao động cùng phương, có phương trình li độ lần lượt là (x1 và x2 tính bằng cm; t tính bằng giây). Tại các thời điểm x1 = x2 và gia tốc của chúng đều âm thì li độ của dao động tổng hợp là:
- (A) -4,8cm.
- (B) 5,19cm.
- (C) 4,8cm.
- (D) -5,19cm.
Con lắc gồm lò xo có độ cứng k = 100N/m; vật nặng có khối lượng m = 200g và điện tích q = 100μC. Ban đầu vật dao động điều hòa với biên độ A = 5cm theo phương thẳng đứng. Khi vật đi qua vị trí cân bằng người ta thiết lập một điện trường đều thẳng đứng, hướng lên có cường độ E = 0,12 MV/m. Tìm biên độ lúc sau của vật trong điện trường.
- (A) 7cm
- (B) 18cm
- (C) 12,5cm
- (D) 13cm.
Hai lò xo nhẹ k1, k2 cùng độ dài được treo thẳng đứng đầu trên cố định, đầu dưới có treo các vật m1 và m2 (m1 = 4m2). Cho m1 và m2 dao động với biên độ nhỏ theo phương thẳng đứng, khi đó chu kì dao động của chúng lần lượt là T1 = 0,6s và T2 = 0,4s. Mắc hai lò xo k1, k2 thành một lò xo dài gấp đôi, đầu trên cố định, đầu dưới treo vật m2. Tần số dao động của m2 khi đó bằng:
- (A) 2,4Hz.
- (B) 2Hz.
- (C) 1Hz.
- (D) 0,5Hz.
Hai con lắc lò xo nằm ngang có chu kì T1 = T2/2. Kéo lệch các vật nặng tới vị trí cách vị trí cân bằng của chúng một đoạn A như nhau và đồng thời thả cho chuyển động không vận tốc ban đầu. Khi khoảng cách từ vật nặng của con lắc đến vị trí cân bằng của chúng đều là b (0 < b < A) thì tỉ số độ lớn vận tốc của các vật nặng là:
- (A) v 1/v 2 = 1/2
- (B) v 1/v 2 = √2 /2
- (C) v 1/v 2 = √2
- (D) v 1/v 2 = 2
Một con lắc đơn có chiều dài 1m được treo dưới gầm cầu cách mặt nước 12m. Con lắc đơn dao động điều hòa với biên độ góc α0 = 0,1rad. Khi vật qua vị trí cân bằng thì dây bị đứt. Khoảng cách cực đại (tính theo phương ngang) từ điểm treo con lắc đến điểm mà vật nặng rơi trên mặt nước mà con lắc có thể đạt được là:
- (A) 49cm.
- (B) 95cm.
- (C) 65cm.
- (D) 85cm.
Một chất điểm dao động điều hòa với chu kì T và biên độ A. Trong khoảng thời gian Δt (0 < Δt < T/2) quãng đường ngắn nhất và dài nhất vật đi được là
- (A)
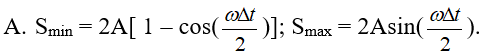
- (B)
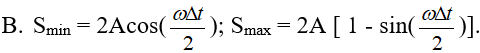
- (C)
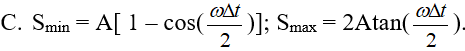
- (D)
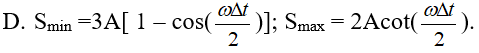
Trong dao động điều hòa của một vật, khoảng thời gian trong một chu kì của vật để vận tốc của vật có độ lớn |v| ≤ 0,5vmax là:
- (A) T/3
- (B) T/4
- (C) T/5
- (D) T/6
Một vật nhỏ dao động điều hòa, gọi t1, t2 và t3 lần lượt là ba thời điểm liên tiếp vật có cùng tốc độ. Biết rằng t3 – t1 = 3(t3 – t2) = 0,1s và v1 = v2 = -v3 = 20π cm/s. Tính biên độ dao động của vật.
- (A) 4cm.
- (B) 5cm.
- (C) 3cm.
- (D) 2cm.
Một vật dao động điều hòa với chu kì T và biên độ A = 4cm. Biết rằng trong một chu kì, khoảng thời gian để gia tốc của vật thỏa mãn -60π2 ≤ a ≤ 80π2 cm/s2 là T/2. Chu kì dao động của con lắc:
- (A) 0,3s.
- (B) 0,4s.
- (C) 0,5s.
- (D) 0,6s.
Một vật dao động điều hòa trên một đoạn thẳng xung quanh vị trí cân bằng O. Gọi M, N là hai điểm trên đường thẳng cùng cách đều điểm O. Biết cứ 0,05s thì chất điểm lại đi qua các điểm M, O, N và tốc độ của nó khi đi qua các điểm M, N là 20π cm/s. Biên độ A của dao động là:
- (A) 4cm.
- (B) 6cm.
- (C) 4 √2 cm.
- (D) 4 √3 cm.
Một con lắc lò xo dao động điều hòa với phương trình x = Acos(ωt + φ) cm. Tại thời điểm t1, vật có vận tốc v1 = 50 cm/s, gia tốc a1 = -10√3 m/s2. Tại thời điểm t2 = t1 + Δt (Δt > 0), vật có vận tốc là v2 = -50√2 cm/s, gia tốc a2 = 10√2 m/s2. Gía trị nhỏ nhất của Δt:
- (A)
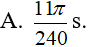
- (B)
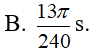
- (C)
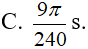
- (D)
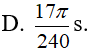
Một vật đồng thời thực hiện ba dao động điều hòa cùng phương, cùng tần số tương ứng là (1), (2) và (3). Dao động (1) ngược pha và có năng lượng gấp đôi dao động (2). Dao động tổng hợp (13) có năng lượng là 3W. Dao động tổng hợp (23) có năng lượng W và vuông pha với dao động (1). Dao động tổng hợp của vật có năng lượng gần nhất với giá trị nào sau đây?
- (A) 2,7W
- (B) 3,3W
- (C) 2,3W
- (D) 1,7W
Một vật tham gia đồng thời hai dao động điều hòa kết hợp ngược pha nhau. Tại thời điểm li độ của dao động thành phần thứ nhất và dao động tổng hợp lần lượt là 2cm và – 3cm. Ở thời điểm ly độ dao động tổng hợp là 4,5cm thì li độ của thành phần thứ hai là:
- (A) – 3cm.
- (B) -7,5cm.
- (C) 7,5cm.
- (D) 3cm.
Hai chất điểm thực hiện dao động điều hòa trên hai đường thẳng song song nằm ngang, có gốc tọa độ nằm cùng trên một đường thẳng có phương thẳng đứng. Phương trình dao động của các chất điểm tương ứng là x1 = A1cos(πt + π/6) cm và x2 = A2cos(πt + π/2) cm (gốc thời gian là lúc hai vật bắt đầu chuyển động). Trong quá trình dao động, khoảng cách theo phương ngang giữa hai chất điểm được biểu diễn bằng phương trình d = Acos(ωt + φ) cm. Thay đổi A1 đến khi biên độ A đạt giá trị cực tiểu thì:
- (A) φ = - π/6 rad.
- (B) φ = - π/3 rad.
- (C) φ = 0 rad.
- (D) φ = π rad.
Một con lắc lò xo được treo thẳng đứng. Trong quá trình dao động người ta quan sát đo đạc và thấy được lò xo không bị biến dạng tại vị trí gia tốc của lò xo có giá trị bằng một nửa giá trị cực đại. Tỉ số giữa thời gian lò xo nén và giãn là:
- (A) 1/2
- (B) 1/3
- (C) 1/4
- (D) 1/5
Một con lắc lò xo được treo thẳng đứng dao động điều hòa với chu kì 1s. Sau 2,5s kể từ lúc bắt đầu dao động, vật có li độ x= -5√2 cm đi theo chiều âm với tốc độ 10π√2 cm/s. Biết lực đàn hồi nhỏ nhất bằng 6N. Chọn trục Ox trùng với trục của lò xo, gốc tọa độ O ở vị trí cân bằng, chiều dương hướng xuống. Lấy g = 10 = π2 m/s2. Lực đàn hồi của lò xo tác dụng vào vật tại thời điểm t = 0 là:
- (A) 1,228N.
- (B) 7,18N.
- (C) 8,71N.
- (D) 12,82N.
Một con lắc đơn gồm vật nặng có khối lượng m gắn với dây treo có chiều dài l. Từ vị trí cân bằng kéo lệch sợi dây sao cho góc lệch của sợi dây với phương thẳng đứng là α0 = 60o rồi thả nhẹ. Lấy g = 10m/s2. Bỏ qua mọi ma sát. Độ lớn của gia tốc khi lực căng dây có độ lớn bằng trọng lực
- (A)
- (B)
- (C)
- (D)
Một con lắc lò xo dao động theo phương thẳng đứng với phương trình x = 5cos(5πt + π) cm. Biết lò xo có độ cứng 100N/m và gia tốc trọng trường tại nơi đặt con lắc là g = 10 = π2. Trong một chu kì, khoảng thời gian lực đàn hồi tác dụng lên vật nặng có độ lớn |Fđh| > 1,5N là:
- (A) 0,249s.
- (B) 0,151s.
- (C) 0,267s.
- (D) 0,3s.
Một con lắc lò xo dao động điều hòa theo phương ngang với năng lượng dao động là 20mJ và lực đàn hồi cực đại là 2N. Gọi I là điểm cố định của lò xo. Khoảng thời gian ngắn nhất từ khi I chịu tác dụng của lực kéo đến khi I chịu tác dụng của lực đẩy có cùng độ lớn 1N là 0,1s. Quãng đường ngắn nhất mà vật đi được trong 0,2s là:
- (A) 2cm.
- (B) (2 - √3 )cm.
- (C) 2 √3 cm.
- (D) 1cm.
Một con lắc lò xo treo thẳng đứng, từ vị trí cân bằng kéo vật xuống phía dưới để lò xo giãn 10cm rồi thả nhẹ. Sau khoảng thời gian nhỏ nhất tương ứng là Δt1, Δt2 thì lực phục hồi và lực đàn hồi của lò xo bị triệt tiêu, với. Lấy g = 10m/s2. Chu kì dao động của con lắc là:
- (A) 0,68s.
- (B) 0,15s.
- (C) 0,76s.
- (D) 0,44s.
Một con lắc đơn dao động điều hòa với chu kì T0 trong chân không. Tại nơi đó, đưa con lắc ra ngoài không khí ở cùng một nhiệt độ thì chu kì của con lắc là T. Biết T khác T0 chỉ do lực đẩy Acsimet của không khí. Gọi tỉ số giữa khối lượng riêng của không khí và khối lượng riêng của chất làm vật nặng là ε. Mối liên hệ giữa T và T0 là:
- (A)
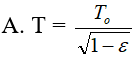
- (B)
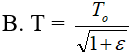
- (C)
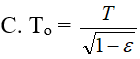
- (D)
Ba con lắc lò xo đặt thẳng đứng 1, 2 và 3. Vị trí cân bằng của ba vật cùng nằm trên một đường thẳng. Chọn trục Ox có phương thẳng đứng, gốc tọa độ ở vị trí cân bằng thì phương trình dao động lần lượt là x1 = A1cos(20t + φ1) cm, x2 = 5cos(20t + π/6) cm và x3 = 10√3cos(20t - π/3) cm. Để ba vật dao động của ba con lắc luôn nằm trên một đường thẳng thì:
- (A) A1 = 10cm và φ1 = π/4 rad.
- (B) A1 = 10cm và φ1 = - π/4 rad.
- (C) A1 = 20cm và φ1 = π/2 rad.
- (D) A1 = 20cm và φ1 = - π/2 rad.
Ba chất điểm dao động điều hòa với cùng biên độ A, cùng một vị trí cân bằng với tần số góc lần lượt là ω, 2ω và 3ω. Biết rằng tại mọi thời điểm. Tại thời điểm t, tốc độ của các chất điểm lần lượt là 10 cm/s; 15 cm/s và v3 = ?
- (A) 20 cm/s.
- (B) 18 cm/s.
- (C) 24 cm/s.
- (D) 25 cm/s.
Đồ thị li độ theo thời gian của chất điểm 1 (đường 1) và chất điểm 2 (đường 2) như hình vẽ, tốc độ cực đại của chất điểm 2 là 4π cm/s. Không kể thời điểm t = 0, thời điểm hai chất điểm có cùng li độ lần thứ 5 là:
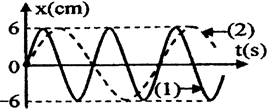
- (A) 4,0s
- (B) 3,25s
- (C) 3,75s
- (D) 3,5s
Một lò xo đồng chất, tiết diện đều được cắt thành ba lò xo có chiều dài tự nhiên là l cm, (l – 10)cm và (l – 20)cm. Lần lượt gắn mỗi lò xo này (theo thứ tự trên) với vật nhỏ khối lượng m thì được ba con lắc có chu kì dao động riêng tương ứng là : 2s; √3s và T. Biết độ cứng của các lò xo tỉ lệ nghịch với chiều dài tự nhiên của nó. Giá trị của T:
- (A) 1,00s
- (B) 1,28s
- (C) 1,41s
- (D) 1,50s
Một lò xo nhẹ có độ cứng 20N/m, đầu trên được treo vào một điểm cố định, đầu dưới gắn vào vặt nhỏ A có khối lượng 100g; vật A được nối với vật nhỏ B có khối lượng 100g bằng một sợi dây mềm, mảnh, nhẹ, không dãn và đủ dài. Từ vị trí cân bằng của hệ, kéo vật B thẳng đứng xuống dưới một đoạn 20cm rồi thả nhẹ để vật B đi lên với vận tốc ban đầu bằng không. Khi vật B bắt đầu đổi chiều chuyển động thì bất ngờ bị tuột tay khỏi dây nối. Bỏ qua các lực cản, lấy g = 10m/s2. Khoảng thời gian từ khi vật B bị tuột khỏi dây nối đến khi rơi đến vị trí được thả ban đầu là:
- (A) 0,30s
- (B) 0,68s
- (C) 0,26s
- (D) 0,28s
Một lò xo đang dao động điều hòa, lực đàn hồi và chiều dài của lò xo có mối liên hệ được cho bởi đồ thị như hình vẽ, cho g = 10 m/s2. Biên độ và chu kì dao động của con lắc là:
- (A) A = 8cm; T = 0,56s.
- (B) A = 6cm; T = 0,28s.
- (C) A = 4cm; T = 0,28s.
- (D) A = 6cm; T = 0,56s.
Một lò xo nhẹ độ cứng k = 20N/m đặt thẳng đứng, đầu dưới gắn cố định, đầu trên gắn với một cái đĩa nhỏ khối lượng M = 600g. Một vật nhỏ khối lượng m = 200g được thả rơi tự do từ độ cao h = 20cm so với đĩa. Coi va chạm hoàn toàn không đàn hồi (va chậm mềm). Chọn t = 0 ngay lúc va chạm, gốc tọa độ tại vị trí cân bằng của hệ vật (M + m), chiều dương hướng xuống, lấy g = 10m/s2. Phương trình dao động của hệ vật là:
- (A) x = 20 √2 cos(5t - π/4 ) cm.
- (B) x = 10 √2 cos(5t + π/4 ) cm.
- (C) x = 10 √2 cos(5t - π/4 ) cm.
- (D) x = 20 √2 cos(5t - π/4 ) cm.
Một con lắc lò xo nằm ngang có chiều dài tự nhiên l0 = 100cm dao động điều hòa trên đoạn thẳng có độ dài l0/10. Tại thời điểm ban đầu, vật đang đi theo chiều dương (là chiều lò xo giãn), lực kéo về có độ lớn cực tiểu thì gia tốc của con lắc là a1 và khi vật có động năng gấp ba lần thế năng lần thứ ba thì gia tốc của con lắc là a2. Khi con lắc có gia tốc là thì chiều dài lò xo lúc đó là:
- (A) 101,25cm.
- (B) 103,75cm.
- (C) 98,75cm.
- (D) 97,25cm .
Hai con lắc lò xo giống nhau đều có khối lượng vật nhỏ là m. Lấy mốc thế năng tại vị trí cân bằng và π2 = 10. X1 và X2 lần lượt là đồ thị li độ theo thời gian của con lắc thứ nhất và con lắc thứ 2 (hình vẽ). Tại thời điểm t, con lắc thứ nhất có động năng 0,06J và con lắc thứ hai có thế năng 0,005J. Giá trị của m là:
- (A) 800g.
- (B) 200g.
- (C) 100g.
- (D) 400g.
Hai con lắc đơn có cùng khối lượng vật nặng được treo vào hai điểm gần nhau cùng một độ cao, cho hai con lắc dao động điều hòa trong hai mặt phẳng song song. Chu kì dao động của con lắc thứ nhất bằng hai lần chu kì dao động của con lắc thứ hai và biên độ dao động của con lắc thứ hai bằng hai lần biên độ dao động của con lắc thứ nhất. Tại một thời điểm hai sợi dây treo song song với nhau thì con lắc thứ nhất có động năng bằng ba lần thế năng, khi đó tỉ số độ lớn vận tốc của con lắc thứ hai và con lắc thứ nhất là:
- (A) 2/ √85
- (B) √85/2
- (C) √5/2
- (D) 2 √5
Dao động của một vật là tổng hợp của hai dao động điều hòa cùng phương, cùng tần số với các biên độ lần lượt là 4cm và 7cm. Biên độ dao động của vật không thể nhận giá trị nào dưới đây?
- (A) 3,5cm.
- (B) 2cm.
- (C) 6cm.
- (D) 8cm.
Cho hai dao động điều hoà với li độ x1 và x2 có đồ thị như hình vẽ. Tổng tốc độ của hai dao động ở cùng một thời điểm có giá trị lớn nhất là:
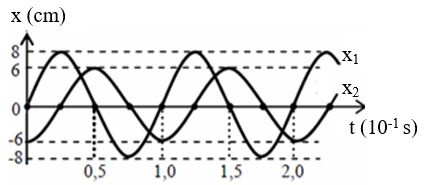
- (A) 280π cm/s.
- (B) 200π cm/s.
- (C) 140π cm/s.
- (D) 20π cm/s.
Hai vật dao động điều hòa dọc theo hai đường thẳng song song kề nhau và song song với trục tọa độ Ox sao cho không va chạm vào nhau trong quá trình dao động. Vị trí cân bằng của hai vật đều ở trên một đường thẳng qua gốc tọa độ và vuông góc với Ox. Biết phương trình dao động của hai vật lần lượt là x1 = 4cos(4πt + π/3) cm và x2 = 4√2 cos(4πt + π/12) cm. Tính từ thời điểm t1 = 1/24 s đến thời điểm t2 = 1/3 s thì thời gian mà khoảng cách giữa hai vật theo phương Ox không nhỏ hơn 2√3 cm là bao nhiêu?
- (A) 1/8 s.
- (B) 1/12 s.
- (C) 1/9 s.
- (D) 1/6 s.
Cho một con lắc đơn có vật nặng được tích điện dao động trong điện trường đều có phương thẳng đứng thì chu kỳ dao động nhỏ là 2,00s. Nếu đổi chiều điện trường, giữ nguyên cường độ thì chu kỳ dao động nhỏ là 3,00s. Chu kỳ dao động nhỏ của con lắc đơn khi không có điện trường là:
- (A) 2,35s.
- (B) 2,50s.
- (C) 1,80s.
- (D) 2,81s.
Con lắc lò xo có độ cứng k, chiều dài l , một đầu gắn cố định, một đầu gắn vào vật có khối lượng m. Kích thích cho lò xo dao động điều hoà với biên độ A = l/ 2 trên mặt phẳng ngang không ma sát. Khi lò xo đang dao động và bị giãn cực đại, tiến hành giữ chặt lò xo tại vị trí cách vật một đoạn l , khi đó tốc độ dao động cực đại của vật là:
- (A)
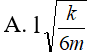
- (B)
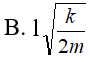
- (C)
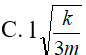
- (D)
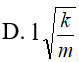
Cho hai dao động điều hoà với li độ x1 và x2 có đồ thị như hình vẽ. Tổng tốc độ của hai dao động ở cùng một thời điểm có giá trị lớn nhất là:
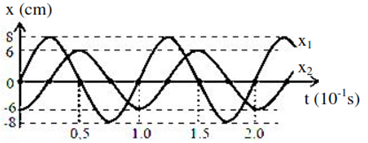
- (A) 200 π c m/s.
- (B) 140 π c m/s.
- (C) 280 π c m/s.
- (D) 100 π c m/s.
Một con lắc lò xo gồm vật nhỏ khối lượng 0,1kg và lò xo có độ cứng 10N/m. Vật nhỏ được đặt trên giá đỡ cố định nằm ngang dọc theo trục lò xo. Hệ số ma sát trượt giữa giá đỡ và vật nhỏ là 0,15. Ban đầu giữ vật ở vị trí lò xo bị nén 7cm rồi buông nhẹ để con lắc dao động tắt dần. Lấy g = 10m/s2. Khi vật dừng lại thì lò xo:
- (A) bị né n 1c m.
- (B) bị dã n 1,5c m.
- (C) bị dã n 1c m.
- (D) bị né n 1,5c m.
Quả cầu kim loại của con lắc đơn có khối lượng m = 0,1kg tích điện q = 10-7C được treo bằng một sợi dây không giãn, mảnh, cách điện có chiều dài l tại nơi có gia tốc trọng trường g = 9,8m/s2 và được đặt trong một điện trường đều, nằm ngang có cường độ E = 2.106V/m. Ban đầu người ta giữ quả cầu để sợi dây có phương thẳng đứng rồi buông nhẹ cho vật dao động điều hòa. Lực căng cực đại của dây trong quá trình dao động là:
- (A) 1,02N.
- (B) 1,04N.
- (C) 1,36N.
- (D) 1,39N.
Đồ thị vận tốc - thời gian của một vật dao động điều hoà như hình vẽ. Phát biểu nào sau đây là đúng?
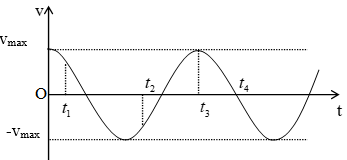
- (A) Tại thời điểm t2, gia tốc của vật có giá trị âm.
- (B) Tại thời điểm t 1, gia tốc của vật có giá trị dương.
- (C) Tại thời điểm t4, vật ở biên dương.
- (D) Tại thời điểm t3, vật ở biên dương.
Một chất điểm tham gia đồng thời hai dao động trên trục Ox có phương trình x1=A1cos10t; x2=A2cos(10t+j2). Phương trình dao động tổng hợp x = A1√3 cos(10t +j), trong đó có j2 - j = π/6. Tỉ số φ/φ2 bằng:
- (A) 1/2 hoặc 3/4
- (B) 1/3 hoặc 2/3
- (C) 3/4 hoặc 2/5
- (D) 2/3 hoặc 4/3
Một con lắc đơn có chiều dài dây treo l = 0,249m, quả cầu nhỏ có khối lượng m = 100g. Cho nó dao động tại nơi có gia tốc trọng trường g = 9,8m/s2 với biên độ góc α0 = 0,07rad trong môi trường dưới tác dụng của lực cản (có độ lớn không đổi) thì nó sẽ dao động tắt dần với cùng chu kì như khi không có lực cản. Biết con lắc đơn chỉ dao động được 100s thì ngừng hẳn. Độ lớn của lực cản bằng:
- (A) 1,7.10 -3N.
- (B) 2,7.10 -4N.
- (C) 1,7.10 -4N.
- (D) 1,2.10 -4N.