📁 Chuyên mục: Tài nguyên trắc nghiệm phần Dao động cơ
📅 Ngày tải lên: 20/10/2024
📥 Tên file: trac nghiem dao dong dieu hoa-54637-thuvienvatly.doc (425KB)
🔑 Chủ đề: trac nghiem dao dong dieu hoa
200 câu trắc nghiệm Dao động điều hòa cực hay, có đáp án
- (A) Chuyển động phóng lên của tên lửa
- (B) Chuyển động của rơi xuống của hạt mưa
- (C) Chuyển động trái đất xung quanh mặt trời
- (D) Chuyển động của tàu tốc hành từ Nam ra Bắc
- (A) Trái đất tự quay quanh trục.
- (B) Các hành tinh quay quanh mặt trời
- (C) Chuyển động của kim la bàn (kim chỉ Nam).
- (D) Chuyển động của các kim đồng hồ.
Đồ thị của dao động điều hòa là
- (A) một đường hình sin.
- (B) một đường thẳng.
- (C) một đường elip.
- (D) một đường parabol.
Một vật nhỏ dao động điều hòa theo một quỹ đạo có chiều dài 10 cm. Biên độ của dao động là
- (A) 10 cm.
- (B) 5 cm.
- (C) 2,5 cm.
- (D) 1,125 cm.
Vật có đồ thị li độ dao động như hình vẽ.
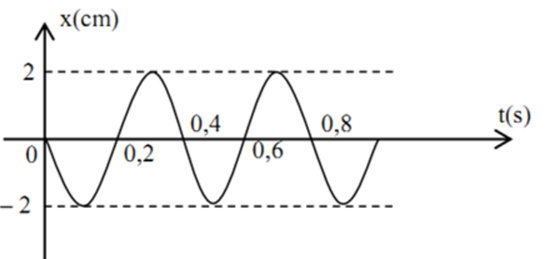
Biên độ và chu kì của vật là:
- (A) A = 2 cm, T = 0,8 s.
- (B) A = 4 cm, T = 0,4 s.
- (C) A = 2 cm, T = 0,4 s.
- (D) A = 4 cm, T = 0,8 s.
Chọn phát biểu sai trong các phương án sau:
- (A) Dao động điều hòa thì tuần hoàn.
- (B) Dao động là chuyển động qua lại quanh một vị trí đặc biệt gọi là vị trí cân bằng.
- (C) Dao động điều hòa là dao động trong đó li độ của vật là một hàm tan (hay cotan) của thời gian.
- (D) Dao động tuần hoàn là dao động mà trạng thái của vật được lặp lại như cũ, theo hướng cũ sau những khoảng thời gian bằng nhau xác định.
- (A) 2 cm.
- (B) 4 cm.
- (C) - 2 cm.
- (D) - 4 cm.
Một vật dao động với phương trình x = 5cos(4πt + ) cm. Tại thời điểm t = 1 s hãy xác định li độ của dao động.
- (A) 2,5 cm.
- (B) 5 cm.
- (C) cm.
- (D) cm.
Pha của dao động được dùng để xác định
- (A) trạng thái dao động.
- (B) biên độ dao động.
- (C) chu kì dao động.
- (D) tần số dao động.
Một vật dao động điều hòa trên quỹ đạo dài 6cm. Biết cứ 2s vật thực hiện được một dao động, tại thời điểm ban đầu vật đang ở vị trí biên dương. Xác định phương trình dao động của vật.
- (A) x = 3cos(πt + π) cm.
- (B) x = 3cos(πt) cm.
- (C) x = 6cos(πt + π) cm.
- (D) x = 6cos(πt) cm.
Phương trình vận tốc của vật là: v = Aωcos(ωt). Phát biểu nào sau đây là đúng?
- (A) Gốc thời gian lúc vật có li độ x = -A
- (B) Gốc thời gian lúc vật có li độ x = A
- (C) Gốc thời gian lúc vật đi qua VTCB theo chiều dương.
- (D) Cả A và B đều đúng.
- (A) 2 cm.
- (B) 4 cm.
- (C) - 2 cm.
- (D) - 4 cm.
Cơ năng của một vật dao động điều hòa
- (A) biến thiên tuần hoàn theo thời gian với chu kỳ bằng một nửa chu kỳ dao động của vật.
- (B) tăng gấp đôi khi biên độ dao động của vật tăng gấp đôi.
- (C) bằng động năng của vật khi vật tới VTC
- (D) biến thiên tuần hoàn theo thời gian với chu kỳ bằng chu kỳ dao động của vật.
Khi nói về năng lượng của một vật dao động điều hòa, phát biểu nào sau đây là đúng?
- (A) Thế năng và động năng của vật được bảo toàn trong quá trình dao động.
- (B) Cơ năng của vật biến thiên tuần hoàn theo thời gian.
- (C) Động năng của vật đạt cực đại khi vật ở vị trí biên.
- (D) Thế năng của vật đạt cực đại khi vật ở vị trí biên.
Một chất điểm dao động điều hòa trên trục Ox. Khi chất điểm đi từ vị trí biên về vị trí cân bằng thì
- (A) thế năng của chất điểm giảm.
- (B) động năng của chất điểm tăng.
- (C) cơ năng được bảo toàn.
- (D) Cả A, B và C đều đúng.
Một con lắc đơn dao động điều hòa với biên độ góc . Lấy mốc thế năng ở vị trí cân bằng. Ở vị trí con lắc có động năng bằng thế năng thì li độ góc của nó bằng:
- (A) .
- (B) .
- (C) .
- (D) .
Một con lắc lò xo gồm lò xo nhẹ và vật nhỏ khối lượng 100g đang dao động điều hòa theo phương ngang, mốc tính thế năng tại vị trí cân bằng. Từ thời điểm đến, động năng của con lắc tăng từ 0,096 J đến giá trị cực đại rồi giảm về 0,064 J. Ở thời điểm t2, thế năng của con lắc bằng 0,064 J. Biên độ dao động của con lắc là
- (A) 6 cm.
- (B) 7 cm.
- (C) 8 cm.
- (D) 9 cm.
Một vật nhỏ có khối lượng m dao động điều hòa trên trục Ox, mốc thế năng tại vị trí cân bằng. Khi gia tốc của vật có độ lớn bằng một nửa độ lớn gia tốc cực đại thì tỉ số giữa thế năng và động năng là
- (A) .
- (B) 2.
- (C) 3.
- (D) .
Một con lắc lò xo dao động điều hòa. Biết lò xo có độ cứng 36 N/m và vật nhỏ có khối lượng 100g. Lấy π2 = 10 . Động năng của con lắc biến thiên theo thời gian với tần số
- (A) 6 Hz.
- (B) 12 Hz.
- (C) 1 Hz.
- (D) 3 Hz.
Một con lắc lò xo nằm ngang, một đầu cố định, một đầu gắn với vật khối lượng 100 g dao động theo phương trình x = 8cos(10t ) ( x tính băng cm, t tính bằng s). Thế năng cực đại của vật là:
- (A) 16 mJ.
- (B) 320 mJ.
- (C) 128 mJ.
- (D) 32 mJ.
Khi nói về năng lượng của một vật dao động điều hòa, phát biểu nào sau đây là đúng ?
- (A) Thế năng của vật đạt giá trị cực đại khi vật đi qua vị trí cân bằng.
- (B) Cơ năng của vật biến thiên tuần hoàn với chu kì bằng 1/2 chu kì dao động điều hòa.
- (C) Thế năng và động năng của vật biến thiên tuần hoàn với cùng tần số.
- (D) Trong mỗi chu kì dao động của vật có hai thời điểm ứng với lúc thế năng bằng động năng.
Con lắc lò xo gồm vật nhỏ khối lượng 100g gắn với một lò xo nhẹ. Con lắc dao động điều hòa theo phương ngang với phương trình x = 10cos10πt (cm). Mốc thế năng ở vị trí cân bằng. Lấy π2 = 10. Cơ năng của con lắc bằng :
- (A) 0,10 J.
- (B) 0,50 J.
- (C) 0,05 J.
- (D) 1,00 J.
Một con lắc lò xo gồm lò xo nhẹ và vật nhỏ khối lượng 100g đang dao động điều hòa theo phương ngang, mốc tính thế năng tại vị trí cân bằng. Từ thời điểm đến , động năng của con lắc tăng từ 0,096 J đến giá trị cực đại rồi giảm về 0,064 J. Ở thời điểm t2, thế năng của con lắc bằng 0,064 J. Biên độ dao động của con lắc là
- (A) 6 cm.
- (B) 7 cm.
- (C) 8 cm.
- (D) 9 cm.
Một con lắc đơn dao động điều hòa với biên độ góc . Lấy mốc thế năng ở vị trí cân bằng. Ở vị trí con lắc có động năng bằng thế năng thì li độ góc của nó bằng:
- (A) .
- (B) .
- (C) .
- (D) .
Một vật dao động điều hòa với biên độ A thì cơ năng của vật
- (A) bằng 0,5 lần thế năng của vật ở li độ .
- (B) bằng 2 lần thế năng của vật ở li độ .
- (C) bằng lần thế năng của vật ở li độ .
- (D) bằng lần thế năng của vật ở li độ .
Một chất điểm dao động điều hoà có quỹ đạo là một đoạn thẳng dài 10 cm. Biên độ dao động của chất điểm là
- (A) 5 cm.
- (B) -5 cm.
- (C) 10 cm.
- (D) -10 cm.
Một chất điểm dao động điều hoà trong 10 dao động toàn phần chất điểm đi được quãng đường dài 120 cm. Quỹ đạo dao động của vật có chiều dài là
- (A) 6 cm.
- (B) 12 cm.
- (C) 3 cm.
- (D) 9 cm.
Một chất điểm dao động điều hoà với phương trình . Li độ của chất điểm khi pha dao động bằng là
- (A) 5 cm.
- (B) – 5 cm.
- (C) 2,5 cm.
- (D) -2,5 cm.
Một chất điểm dao động điều hoà có phương trình li độ theo thời gian là: . Tại thời điểm thì li độ của chất điểm bằng
- (A)
- (B)
- (C)
- (D)
Một chất điểm dao động điều hoà có phương trình li độ theo thời gian là: . Li độ của chất điểm khi pha dao động bằng là
- (A) 3cm
- (B) -3cm
- (C)
- (D)
Một chất điểm M chuyển động đều trên một đường tròn, bán kính R, tốc độ góc . Hình chiếu của M trên đường kính biến thiên điều hoà có
- (A) biên độ R .
- (B) biên độ 2R .
- (C) pha ban đầu t.
- (D) độ dài quỹ đạo 4R.
Phương trình dao động của một vật có dạng Pha ban đầu của dao động là
- (A)
- (B)
- (C)
- (D)
Một chất điểm dao động theo phương trình x = 6cosωt (cm). Dao động của chất điểm có biên độ là
- (A) 2 cm.
- (B) 6 cm.
- (C) 3 cm.
- (D) 12 cm.
Một chất điểm dao động có phương trình x = 10cos(15t + π) (x tính bằng cm, t tính bằng s). Chất điểm này dao động với tần số góc là
- (A) 20 rad/s.
- (B) 10 rad/s.
- (C) 5 rad/s.
- (D) 15 rad/s.
Một vật nhỏ dao động theo phương trình x = 5cos(ωt + 0,5π) (cm). Pha ban đầu của dao động là
- (A) π .
- (B) 0,5 π .
- (C) 0,25 π .
- (D) 1,5 π
Chu kì dao động là
- (A) thời gian chuyển động của vật.
- (B) thời gian vật thực hiện một dao động toàn phần.
- (C) số dao động toàn phần mà vật thực hiện được.
- (D) số dao động toàn phần mà vật thực hiện trong một giây.
Khi vật thực hiện một dao động tương ứng với pha dao động sẽ thay đổi một lượng
- (A) 0 rad.
- (B) rad.
- (C) rad.
- (D) rad.
- (A)
- (B)
- (C)
- (D)
Đơn vị của tần số dao động trong hệ đơn vị SI là
- (A) Hz
- (B) s.
- (C) cm.
- (D) m.
Một vật đang dao động với chu kì là 0,3 s, tần số dao động của vật là
- (A) 0,3 Hz.
- (B) 0,33 Hz.
- (C) 3,33 Hz.
- (D) 33 Hz.
Khi tiến hành thí nghiệm khảo sát vị trí vật nặng của con lắc lò xo đang dao động bằng cách sử dụng thước thẳng, bạn học sinh thấy rằng vật nặng dao động từ vị trí 1 cm đến vị trí 11 cm trên thước. Biên độ dao động của vật nặng trong con lắc lò xo là
- (A) 10 cm.
- (B) 6 cm.
- (C) 5 cm.
- (D) 12 cm.
Một bạn học sinh quan sát thấy con lắc trong đồng hồ quả lắc thực hiện được 20 dao động trong 30 giây. Dao động của con lắc trong đồng hồ này có đặc điểm nào sau đây?
- (A) Dao động điều hoà, tần số là 1,5 Hz.
- (B) Dao động điều hoà, tần số là 0,7 Hz.
- (C) Dao động tuần hoàn, tần số là 1,5 Hz.
- (D) Dao động tuần hoàn, tần số là 0,7 Hz.
Các nhà thực nghiệm đo được tần số dao động của một hệ gồm thanh silicon siêu nhỏ có virus dính trên đó đang thực hiện dao động là . Tần số góc của hệ dao động trên bằng bao nhiêu?
- (A) .
- (B) .
- (C) .
- (D) .
Một chất điểm dao động điều hoà có chu kì T = 1 s. Tần số góc của dao động là
- (A)
- (B)
- (C)
- (D) 2 (rad/s).
Một chất điểm dao động điều hoà có phương trình li độ theo thời gian là: . Tần số của dao động là
- (A)
- (B)
- (C)
- (D)
Chọn kết luận đúng về dao động điều hoà của con lắc lò xo.
- (A) Quỹ đạo là đường hình sin.
- (B) Quỹ đạo là một đoạn thẳng.
- (C) Vận tốc tỉ lệ thuận với thời gian.
- (D) Gia tốc tỉ lệ thuận với thời gian.
Một vật dao động điều hòa trên trục Ox quanh vị trí cân bằng O. Vectơ gia tốc của vật.
- (A) luôn hướng ra xa vị trí cân bằng.
- (B) có độ lớn tỷ lệ nghịch với độ lớn li độ của vật.
- (C) luôn hướng về vị trí cân bằng.
- (D) có độ lớn tỷ lệ thuận với độ lớn vận tốc của vật.
Vectơ vận tốc của một vật dao động điều hoà luôn
- (A) hướng ra xa VTCB
- (B) cùng hướng chuyển động.
- (C) hướng về VTCB
- (D) ngược hướng chuyển động.
Một chất điểm dao động điều hòa trên trục Ox. Vecto gia tốc của chất điểm có:
- (A) Độ lớn cực tiểu khi đi qua vị trí cân bằng, luôn cùng chiều với vecto vận tốc.
- (B) Độ lớn không đổi, chiều luôn hướng về vị trí cân bằng.
- (C) Độ lớn cực đại ở biên, chiều luôn hướng ra biên.
- (D) Độ lớn tỷ lệ với độ lớn của li độ, chiều luôn hướng về vị trí cân bằng.
Một vật dao động điều hòa với phương trình . Tốc độ cực đại của chất điểm trong quá trình dao động bằng
- (A)
- (B)
- (C)
- (D)
Gia tốc của vật dao động điều hoà bằng không khi :
- (A) vật ở vị trí có li độ cực đại .
- (B) vận tốc của vật đạt cực tiểu.
- (C) vật ở vị trí có li độ bằng không .
- (D) vật ở vị trí có pha dao động cực đại.
Vận tốc trong dao động điều hòa có độ lớn cực đại khi
- (A) li độ có độ lớn cực đại.
- (B) gia tốc cực đại.
- (C) li độ bằng 0.
- (D) li độ bằng biên độ.
Vận tốc của vật dao động điều hoà bằng không khi
- (A) vật ở vị trí có li độ cực đại
- (B) gia tốc của vật đạt cực đại.
- (C) vật ở vị trí có li độ bằng không
- (D) vật ở vị trí có pha dao động cực đại.
Biểu thức nào sau đây là biểu thức tính gia tốc của một vật dao động điều hòa?
- (A) a = 4x.
- (B) a = 4x2.
- (C) a = -4x2.
- (D) a = -4x.
Chọn phát biểu sai về quan hệ giữa chuyển động tròn đều và dao động điều hoà là hình chiếu của nó.
- (A) biên độ của dao động bằng bán kính quỹ đạo của chuyển động tròn đều.
- (B) vận tốc của dao động bằng vận tốc dài của chuyển động tròn đều.
- (C) tần số góc của dao động bằng tốc độ góc của chuyển động tròn đều.
- (D) li độ của dao động bằng toạ độ hình chiếu của chuyển động tròn đều.
Một vật dao động điều hòa với biên độ A = 2 cm, tần số góc 5rad/s pha ban đầu Phương trình dao động của vật là
- (A)
- (B)
- (C)
- (D)
Một vật nhỏ dao động điều hòa dọc theo trục Ox với biên độ 5 cm, chu kỳ 2 s. Tại thời điểm t = 0, vật đi qua vị trí cân bằng theo chiều dương. Phương trình dao động của vật là
- (A)
- (B)
- (C)
- (D)
Một vật nhỏ dao động điều hòa dọc theo trục Ox. Trong thời gian 31,4 s chất điểm thực hiện được 100 dao động toàn phần. Gốc thời gian là lúc chất điểm đi qua vị trí có li độ 2 cm theo chiều âm với tốc độ Lấy phương trình dao động của chất điểm là
- (A)
- (B)
- (C)
- (D)
Một vật nhỏ dao động điều hòa với chu kì T = 2 s. Khi vật cách vị trí cân bằng một khoảng 5 cm thì vật có vận tốc là Chọn mốc thời gian khi vật qua vị trí cân bằng theo chiều âm. Phương trình dao động của vật là
- (A)
- (B)
- (C)
- (D)
Một vật nhỏ dao động điều hòa trên quỹ đạo dài 8 cm. Khi đi qua vị trí cân bằng vận tốc có độ lớn Gọi mốc thời gian là lúc vật đi qua vị trí theo chiều dương. Phương trình dao động của vật là
- (A)
- (B)
- (C)
- (D)
Một vật dao động điều hoà, khoảng thời gian giữa hai lần liên tiếp vật qua vị trí cân bằng là 0,5s quãng đường vật đi được trong 2s là 32cm Gốc thời gian được chọn lúc vật qua li độ theo chiều dương. Phương trình dao động của vật là
- (A)
- (B)
- (C)
- (D)
Một vật dao động điều hoà với chu kì T=2s trong 2s vật đi được quãng đường 40cm Khi t=0 vật đi qua vị trí cân bằng theo chiều dương. Phương trình dao động của vật là
- (A)
- (B)
- (C)
- (D)
Một vật có khối lượng m=1kg dao động điều hoà với chu kỳ 2s Vật qua vị trí cân bằng với vận tốc 0,314m/s Khi t=0vật qua vị trí có li độ theo chiều âm của quỹ đạo. Lấy Phương trình dao động điều hoà của vật là
- (A)
- (B)
- (C)
- (D)
Một vật nhỏ dao động điều hòa có phương trình dạng Tại thời điểm ban đầu vật cách vị trí cân bằng một khoảng 4 cm, vận tốc và gia tốc của vật lúc đó lần lượt là và Phương trình dao động của vật là
- (A)
- (B)
- (C)
- (D)
Một vật nhỏ dao động điều hòa theo trục Ox, chọn gốc tọa độ trùng với vị trí cân bằng của vật. Biết khoảng thời gian giữa hai lần liên tiếp vật đi qua vị trí cân bằng là 1 s. Lấy Tại thời điểm ban đầu vật có gia tốc và vận tốc Phương trình dao động của vật là
- (A)
- (B)
- (C)
- (D)
Khi nói về cơ năng của vật dao động điều hòa, phát biểu nào dưới đây sai?
- (A) Động năng và thế năng biến đổi cùng chu kỳ.
- (B) Động năng biến đổi cùng chu kỳ với vận tốc.
- (C) Tổng động năng và thế năng không thay đổi theo thời gian.
- (D) Thế năng biến đổi với tần số gấp 2 lần tần số của li độ.
Phát biểu nào sau đây là đúng khi nói về năng lượng của vật dao động điều hòa?
- (A) Động năng đạt giá trị lớn nhất khi vật có li độ cực đại.
- (B) Khi vật chuyển động về phía vị trí cân bằng thì thế năng tăng dần.
- (C) Cơ năng của vật dao động tỷ lệ thuận với biên độ.
- (D) Thế năng của vật dao động bằng cơ năng khi vận tốc của vật bằng 0
Phát biểu nào sau đây là sai khi nói về năng lượng của vật dao động điều hòa?
- (A) Khi vật ở vị trí biên thì thế năng của hệ lớn nhất.
- (B) Khi vật đi qua vị trí cân bằng thì động năng của hệ lớn nhất.
- (C) Khi vật chuyển động về vị trí cân bằng thì thế năng của hệ giảm còn động năng của hệ tăng lên.
- (D) Khi động năng của hệ tăng lên bao nhiêu lần thì thế năng của hệ giảm đi bấy nhiêu lần và ngược lại
Phát biểu nào sau đây là sai khi nói về năng lượng của vật dao động điều hòa?
- (A) Khi vật chuyển về vị trí cân bằng thì động năng tăng và thế năng giảm.
- (B) Khi vật ở vị trí cân bằng thì động năng đạt giá trị cực đại.
- (C) Động năng bằng thế năng khi x =
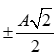
- (D) Khi gia tốc bằng 0 thì thế năng bằng cơ năng
Phát biểu nào sau đây là đúng khi nói về năng lượng của vật dao động điều hòa?
- (A) Động năng của chất điểm biến thiên tuần hoàn theo thời gian.
- (B) Động năng của chất điểm biến thiên điều hòa theo tần số f.
- (C) Động năng của chất điểm biến thiên tuần hoàn theo tần số 2f.
- (D) Động năng của chất điểm là một đại lượng bảo toàn, không phụ thuộc vào thời gian
Phát biểu nào sau đây là không đúng? Cơ năng của một vật dao động điều hoà
- (A) tỉ lệ nghịch với bình phương của chu kỳ dao động.
- (B) bằng thế năng của vật ở vị trí biên.
- (C) tỉ lệ thuận với biên độ dao động.
- (D) bằng động năng của vật khi qua vị trí cân bằng.
Phát biểu nào sau đây là đúng khi nói về năng lượng của vật dao động điều hòa?
- (A) Khi vật chuyển động về vị trí cân bằng thì thế năng của vật tăng.
- (B) Khi động năng của vật tăng thì thế năng cũng tăng.
- (C) Khi vật dao động ở vị trí cân bằng thì động năng của hệ lớn nhất.
- (D) Khi vật chuyển động về vị trí biên thì động năng của vật tăng.
Một con lắc lò xo có độ cứng k và vật nặng có khối lượng m, dao động với biên độ A. Thay vật nặng bằng vật có khối lượng 2m và cũng cho dao động với biên độ bằng A thì năng lượng dao động của vật sẽ
- (A) giảm 4 lần.
- (B) tăng 4 lần.
- (C) tăng 2 lần.
- (D) không đổi.
Trong quá trình dao động điều hòa của con lắc lò xo thì
- (A) cơ năng và động năng biến thiên tuần hoàn cùng tần số, tần số đó gấp đôi tần số dao động.
- (B) sau mỗi lần vật đổi chiều, có 2 thời điểm tại đó cơ năng gấp hai lần động năng.
- (C) khi động năng tăng, cơ năng giảm và ngược lại, khi động năng giảm thì cơ năng tăng.
- (D) cơ năng của vật bằng động năng khi vật đổi chiều chuyển động.
Khi nói về một vật dao động điều hoà với biên độ A và tần số f, trong những phát biểu dưới đây:
(1) Cơ năng biến thiên tuần hoàn với tần số 2f.
(2) Cơ năng bằng thế năng tại thời điểm vật ở biên.
(3) Cơ năng tỉ lệ thuận với biên độ dao động.
(4) Khi vật đi từ vị trí cân bằng ra biên, thế năng giảm, động năng tăng.
(5) Khi vật đi từ biên về vị trí cân bằng, thế năng giảm, động năng tăng.
Số phát biểu đúng là
- (A) 1.
- (B) 3.
- (C) 2 .
- (D) 4.
Động năng dao động của một con lắc lò xo được mô tả theo thế năng dao động của nó bằng đồ thị như hình vẽ dưới đây.
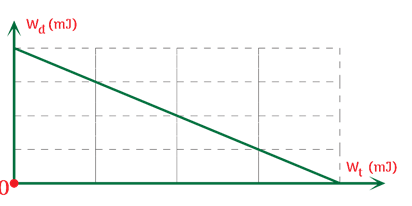
Cho biết khối lượng của vật bằng 100 gam, vật dao động giữa hai vị trí cách nhau 8 cm. Tính tần số góc của dao động của con lắc lò xo.
Hai chất điểm có khối lượng lần lượt là m1, m2 dao động điều hòa cùng phương cùng tần số. Đồ thị biểu diễn động năng của m1 và thế năng của m2 theo li độ như hình vẽ.
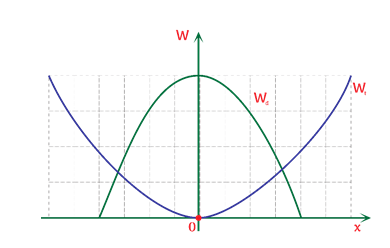
Xác định tỉ số m1/m2.
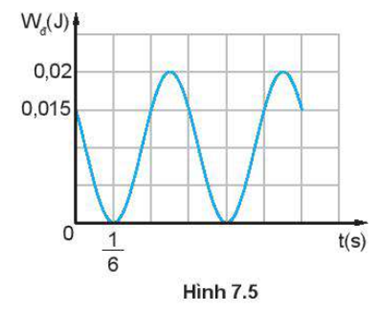
Hình dưới đây là đồ thị động năng theo thời gian của một vật khối lượng 0,4 kg dao động điều hoà.
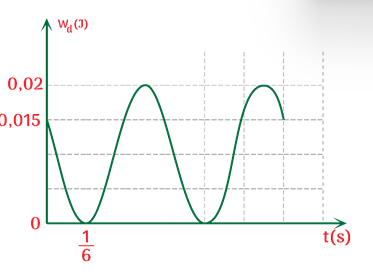
Đồ thị động năng theo thời gian
Tại thời điểm ban đầu vật đang chuyển động theo chiều dương. Lấy π2 = 10. Viết phương trình dao động của vật.
Trong cuộc sống hằng ngày và trong kĩ thuật ta thường gặp những vật dao động, ví dụ như dây đàn ghi ta rung động, chiếc đu đung đưa, pít-tông chuyển động lên xuống trong xi lanh của động cơ,... Chuyển động của những vật này được gọi là dao động cơ. Vậy dao động cơ có những đặc điểm gì chung?
Chuẩn bị:
Sử dụng con lắc lò xo hoặc con lắc đơn (Hình 1.1).
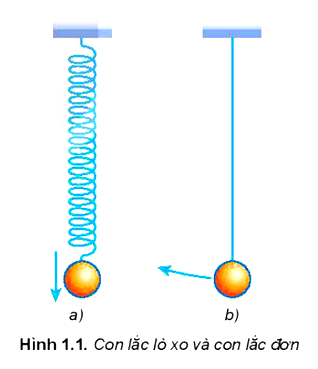
Tiến hành:
Treo một vật nhỏ, nặng vào đầu tự do của một lò xo nhẹ (Hình 1.1a) hoặc một dây nhẹ không dãn ta có con lắc lò xo hoặc con lắc đơn (Hình 1.1b).
1. Xác định vị trí cân bằng của vật.
2. Kéo vật lệch khỏi vị trí cân bằng rồi thả ra cho chuyển động. Quan sát chuyển động của mỗi vật và cho nhận xét về đặc điểm chung của chúng.
Nêu những ví dụ về dao động cơ mà em biết.
Một vật dao động điều hoà có phương trình
Hãy xác định:
a) Biên độ và pha ban đầu của dao động.
b) Pha và li độ của dao động khi t = 2 s.
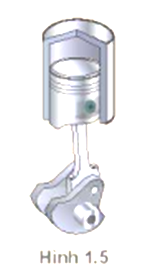
Đồ thị li độ - thời gian của một con lắc đơn dao động điều hoà được mô tả trên Hình 1.3.
1. Hãy mô tả dao động điều hoà của con lắc đơn.
2. Xác định biên độ và li độ của con lắc ở các thời điểm t = 0, t = 0,5 s, t = 2,0 s.
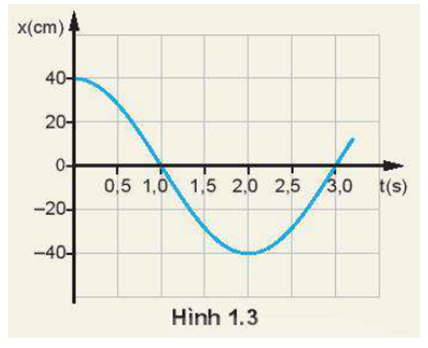
Pít-tông của một động cơ đốt trong dao động trên một đoạn thẳng dài 16 cm và làm cho trục khuỷu của động cơ quay đều (Hình 1.5). Xác định biên độ dao động của một điểm trên mặt pít-tông.
Một chất điểm dao động điều hoà có quỹ đạo là một đoạn thẳng dài 10 cm. Biên độ dao động của chất điểm là
A. 5 cm.
B. -5 cm.
C. 10 cm.
D. -10 cm.
Một chất điểm dao động điều hoà trong 10 dao động toàn phần chất điểm đi được quãng đường dài 120 cm. Quỹ đạo dao động của vật có chiều dài là
A. 6 cm.
B. 12 cm.
C. 3 cm.
D. 9 cm.
Một chất điểm dao động điều hoà với phương trình \(x = 5{\rm{cos}}\left( {10\pi t + \frac{\pi }{3}} \right)\left( {{\rm{cm}}} \right)\). Li độ của chất điểm khi pha dao động bằng \(\left( \pi \right)\) là
A. 5 cm.
B. – 5 cm.
C. 2,5 cm.
D. -2,5 cm.
Một chất điểm dao động điều hoà có phương trình li độ theo thời gian là: \(x = 5\sqrt 3 {\rm{cos}}\left( {10\pi t + \frac{\pi }{3}} \right)\left( {{\rm{cm}}} \right)\). Tại thời điểm \({\rm{t}} = 1{\rm{\;s}}\) thì li độ của chất điểm bằng
B. \( - 5\sqrt 3 {\rm{\;cm}}\).
D. \(2,5\sqrt 3 {\rm{\;cm}}\).
Để vẽ đồ thị hoặc viết phương trình của một dao động điều hoà cần biết những đại lượng vật lí nào?
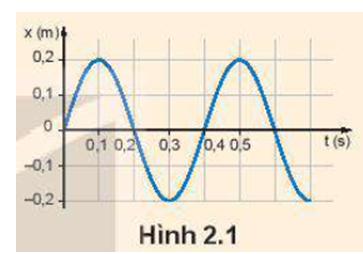
Hình 2.1 là đồ thị dao động điều hoà của một vật.
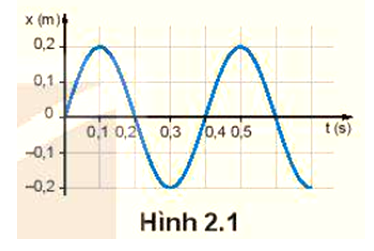
Hãy xác định:
- Biên độ, chu kì, tần số của dao động.
- Nêu thời điểm mà vật có li độ x = 0; x = 0,1 m.
Từ Hình 2.1 hãy xác định tần số góc của dao động của vật.
Hình 2.3 là đồ thị dao động điều hoà của một con lắc.
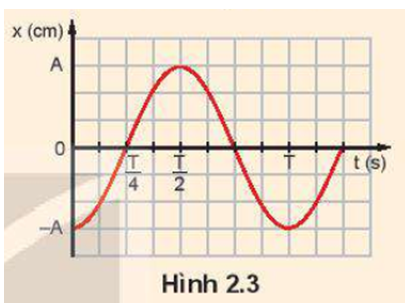
Hãy cho biết:
- Vị trí và hướng dịch chuyển của con lắc tại thời điểm ban đầu.
- Pha ban đầu của dao động.
Hãy chứng minh rằng độ lệch pha giữa hai dao động cùng chu kì bằng độ lệch pha ban đầu.
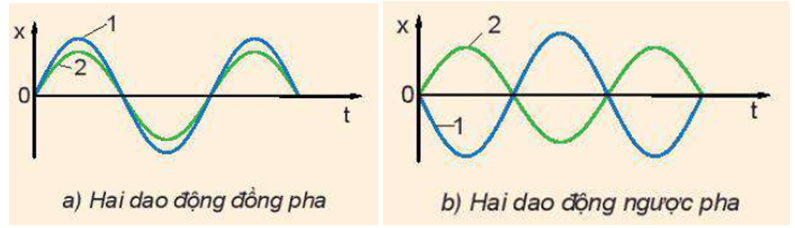
Hai con lắc 1 và 2 dao động điều hoà tại cùng thời điểm quan sát vị trí của chúng được biểu diễn trên Hình 2.5 a, b. Hỏi dao động của con lắc nào sớm pha hơn và sớm hơn bao nhiêu?
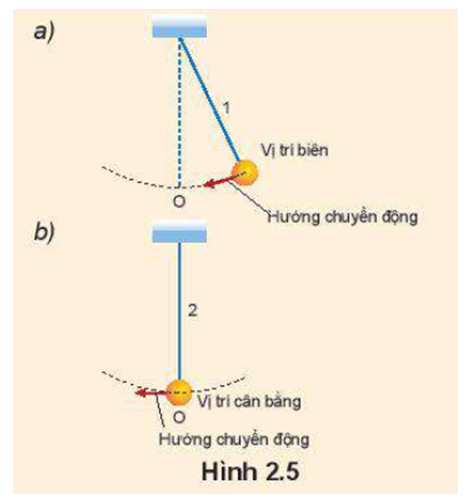
Xét một vật dao động điều hoà có biên độ 10 cm, tần số 5 Hz. Tại thời điểm ban đầu (t = 0) vật có li độ cực đại theo chiều dương.
- Xác định chu kì, tần số góc, pha ban đầu của dao động.
- Viết phương trình và vẽ đồ thị (x - t) của dao động.
Cho hai con lắc đơn dao động điều hoà. Biết phương trình dao động của con lắc thứ nhất là . Con lắc thứ hai có cùng biên độ và tần số nhưng lệch về thời gian so với con lắc thứ nhất một phần tư chu kì. Viết phương trình dao động của con lắc thứ hai.
Đại lượng nào dưới đây đặc trưng cho độ lệch về thời gian giữa hai dao động điều hoà cùng chu kì?
A. Li độ.
B. Pha.
C. Pha ban đầu.
D. Độ lệch pha.
Hãy chứng minh rằng độ lệch pha giữa hai dao động điều hoà cùng tần số là đại lượng không đổi và bằng độ lệch pha ban đầu.
Dùng đồ thị li độ – thời gian có dạng hình sin hoặc phương trình của dao động điều hoà để xác định các đại lượng như biên độ chu kì, tần số, tần số góc và pha ban đầu của dao động đó.
Biết cách xác định độ lệch pha giữa hai dao động điều hoà cùng chu kì.
Một chất điểm dao động điều hoà có chu kì T = 1 s. Tần số góc \(\omega \) của dao động là
A. \(\pi \left( {{\rm{rad}}/{\rm{s}}} \right)\).
B. \(2\pi \left( {{\rm{rad}}/{\rm{s}}} \right)\).
D. 2 (rad/s).
Một chất điểm dao động điều hoà có tần số góc \(\omega = 10\pi \left( {{\rm{rad}}/{\rm{s}}} \right)\). Tần số của dao động là
A. \(5{\rm{\;Hz}}\).
B. \(10{\rm{\;Hz}}\).
C. \(20{\rm{\;Hz}}\).
D. \(5\pi {\rm{Hz}}\).Một chất điểm dao động điều hoà. Trong thời gian 1 phút, vật thực hiện được 30 dao động. Chu kì dao động của chất điểm là
A. \(2{\rm{\;s}}\).
B. \(30{\rm{\;s}}\).
C. \(0,5{\rm{\;s}}\).
D. \(1{\rm{\;s}}\).
Một chất điểm dao động điều hoà có phương trình li độ theo thời gian là: \(x = 5\sqrt 3 {\rm{cos}}\left( {10\pi t + \frac{\pi }{3}} \right)\left( {{\rm{cm}}} \right)\). Tần số của dao động là
A. \(10{\rm{\;Hz}}\).
B. \(20{\rm{\;Hz}}\).
C. \(10\pi {\rm{Hz}}\).
D. \(5{\rm{\;Hz}}\).
Ta có thể dựa vào đồ thị (x – t) của dao động điều hoà để xác định vận tốc và gia tốc của vật được không?
Đặt một thước kẻ (loại 20 cm) cho mép của thước tiếp xúc với đồ thị li độ - thời gian (Hình 3.1) ở một số điểm C, D, E, G, H. Từ độ dốc của thước hãy so sánh độ lớn vận tốc của vật tại các điểm C, E, H.
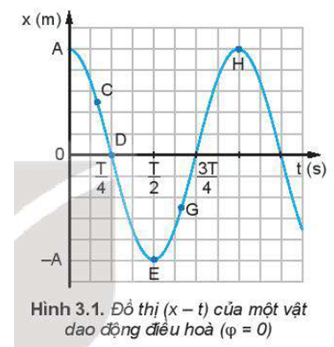
So sánh đồ thị của vận tốc (Hình 3.2) với đồ thị của li độ (Hình 3.1), hãy cho biết vận tốc sớm pha hay trễ pha bao nhiêu so với li độ.
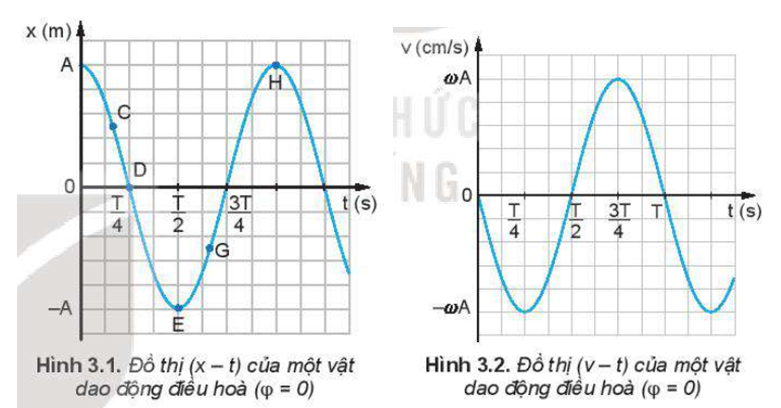
Trong các khoảng thời gian từ 0 đến , từ đến , từ đến , từ đến T, vận tốc của dao động điều hoà thay đổi như thế nào?
Dùng thước kẻ (loại 20 cm) để xác định xem trên đồ thị (v – t) Hình 3.2, tại thời điểm nào độ dốc của đồ thị bằng 0 và tại thời điểm nào độ dốc của đồ thị cực đại. Từ đó, so sánh độ lớn của gia tốc trên đồ thị (a - t) Hình 3.3 ở các thời điểm tương ứng.
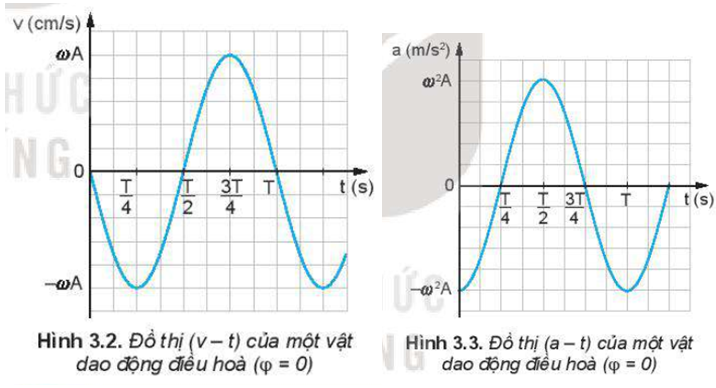
Phương trình dao động của một vật là . Hãy viết phương trình vận tốc, gia tốc và vẽ đồ thị li độ, vận tốc, gia tốc theo thời gian của vật.
So sánh đồ thị Hình 3.3 và Hình 3.1 ta có nhận xét gì về pha của li độ và gia tốc của một dao động.
Trong các khoảng thời gian từ 0 đến , từ đến , từ đến , từ đến T gia tốc của dao động thay đổi như thế nào?
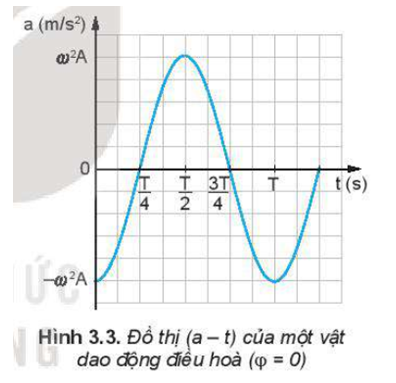
Một vật dao động điều hoà trên trục Ox. Khi vật qua vị trí cân bằng thì tốc độ của nó là 20 cm/s. Khi vật có tốc độ là 10 cm/s thì gia tốc của nó có độ lớn là cm/. Tính biên độ dao động của vật.
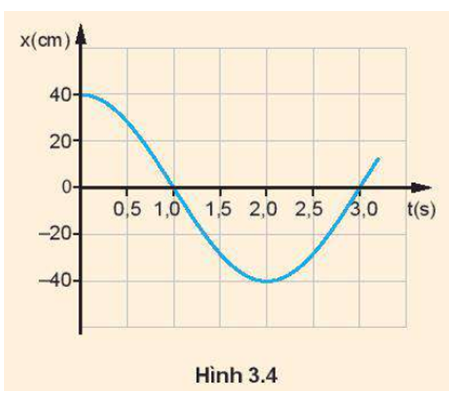
Hình 3.4 là đồ thị li độ – thời gian của một vật dao động điều hoà. Sử dụng đồ thị để tính các đại lượng sau:
a) Tốc độ của vật ở thời điểm t = 0 s.
b) Tốc độ cực đại của vật.
c) Gia tốc của vật tại thời điểm t = 1,0 s.
Sử dụng được đồ thị mô tả dao động điều hoà thu được trên dao động kí có thể suy ra các đại lượng vận tốc, gia tốc của vật trong dao động điều hoà.
Chọn kết luận đúng về dao động điều hoà của con lắc lò xo.
A. Quỹ đạo là đường hình sin.
B. Quỹ đạo là một đoạn thẳng.
C. Vận tốc tỉ lệ thuận với thời gian.
D. Gia tốc tỉ lệ thuận với thời gian.
Một vật dao động điều hoà có phương trình \(x = 2{\rm{cos}}\left( {5t - \frac{\pi }{6}} \right)\left( {{\rm{cm}}} \right)\). Phương trình vận tốc của vật là:
A. \(v = 5{\rm{cos}}\left( {5t - \frac{\pi }{6}} \right)\left( {{\rm{cm}}/{\rm{s}}} \right)\).
B. \(v = 10{\rm{cos}}\left( {5t + \frac{\pi }{3}} \right)\left( {{\rm{cm}}/{\rm{s}}} \right)\).
C. \(v = 20{\rm{cos}}\left( {5t - \frac{\pi }{6}} \right)\left( {{\rm{cm}}/{\rm{s}}} \right)\).
D. \(v = 5{\rm{cos}}\left( {5t + \frac{\pi }{3}} \right)\left( {{\rm{cm}}/{\rm{s}}} \right)\).
Vận tốc của một vật dao động điều hoà tại vị trí cân bằng là \(1{\rm{\;cm}}/{\rm{s}}\) và gia tốc của vật tại vị trí biên là \(1,57{\rm{\;cm}}/{{\rm{s}}^2}\). Chu kì dao động của vật là:
A. 3,24 s.
B. \(6,28{\rm{\;s}}\).
C. \(4{\rm{\;s}}\).
D. \(2{\rm{\;s}}\).
Một chất điểm dao động điều hoà với tần số \(4{\rm{\;Hz}}\) và biên độ \(10{\rm{\;cm}}\). Gia tốc cực đại của chất điểm là:
A. \(2,5{\rm{\;m}}/{{\rm{s}}^2}\).
B. \(25{\rm{\;m}}/{{\rm{s}}^2}\).
C. \(63,1{\rm{\;m}}/{{\rm{s}}^2}\).
D. \(6,31{\rm{\;m}}/{{\rm{s}}^2}\).
Chất điểm \(M\) chuyển động tròn đều trên một đường tròn với tốc độ dài \(160{\rm{\;cm}}/{\rm{s}}\) và tốc độ góc \(4{\rm{rad}}/{\rm{s}}\). Hình chiếu \({\rm{P}}\) của \({\rm{M}}\) trên một đường thẳng cố định nằm trong mặt phẳng hình tròn dao động điều hoà với biên độ và chu kì lần lượt là:
A. \(40{\rm{\;cm}};0,25{\rm{\;s}}\).
B. \(40{\rm{\;cm}};1,57{\rm{\;s}}\).
C. \(40{\rm{\;m}};0,25{\rm{\;s}}\).
D. \(2,5{\rm{\;m}};0,25{\rm{\;s}}\).Phương trình vận tốc của một vật dao động là: \(v = 120{\rm{cos}}20t\left( {{\rm{cm}}/{\rm{s}}} \right)\), đơn vị đo của thời gian \(t\) là giây. Vào thời điểm \(t = \frac{T}{6}\) (T là chu kì dao động), vật có li độ là:
A. \(3{\rm{\;cm}}\).
C. \(3\sqrt 3 {\rm{\;cm}}\).
D. \( - 3\sqrt 3 {\rm{\;cm}}\).
Khi biết phương trình hoặc đồ thị của vật dao động điều hoà, làm thế nào để xác định được vận tốc và gia tốc của vật?
Nếu đề bài cho phương trình dao động không đúng dạng cơ bản thì ta xác định pha ban đầu như thế nào?
Có thể sử dụng mối liên hệ giữa dao động điều hoà và chuyển động tròn đều để xác định pha ban đầu, thời gian để vật đi từ điểm này đến điểm khác trong dao động điều hoà được không?
Một vật dao động điều hoà có phương trình là (cm). Hãy cho biết biên độ, tần số góc, chu kì, tần số, pha ban đầu và pha của dao động ở thời điểm t = 1 s.
Một vật dao động điều hoà dọc theo trục Ox, quanh điểm gốc O, với biên độ A = 10 cm và chu kì T = 2 s. Tại thời điểm t = 0, vật có li độ x = A.
a) Viết phương trình dao động của vật.
b) Xác định thời điểm đầu tiên vật qua vị trí có li độ x = 5 cm.
Hình 4.2 là sơ đồ của một bàn xoay hình tròn, có gắn một thanh nhỏ cách tâm bàn 15 cm. Bàn xoay được chiếu sáng bằng nguồn sáng rộng, song song, hướng chiếu sáng từ phía trước màn để bóng đổ lên màn hình. Một con lắc đơn dao động điều hoà phía sau bàn xoay với biên độ bằng khoảng cách từ thanh nhỏ đến tâm bàn xoay. Tốc độ quay của bàn quay được điều chỉnh là rad/s. Vị trí bóng của thanh nhỏ con lắc luôn trùng nhau.
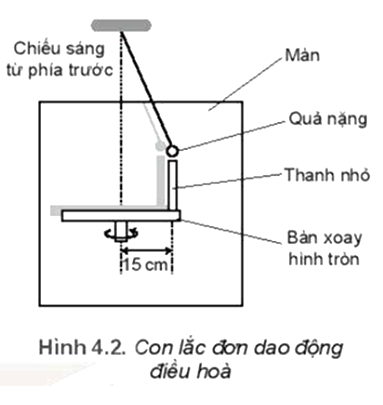
a) Tại sao nói dao động của bóng của thanh nhỏ và quả nặng là đồng pha?
b) Viết phương trình dao động của con lắc. Chọn gốc thời gian là lúc con lắc ở vị trí hiển thị trong Hình 4.2.
c) Bàn xoay đi một góc 60° từ vị trí ban đầu, tính li độ của con lắc và tốc độ của nó tại thời điểm này.
Hình 4.3 là đồ thị li độ – thời gian của một vật dao động điều hoà.
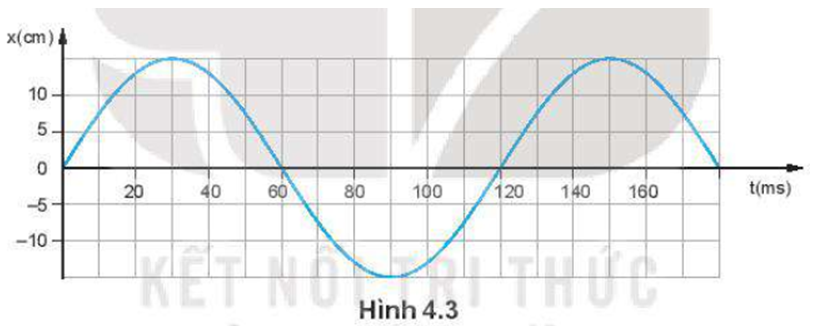
a) Xác định biên độ, chu kì, tần số, tần số góc và pha ban đầu của vật dao động.
b) Viết phương trình của dao động của vật.
Đồ thị li độ – thời gian của hai vật dao động điều hoà A và B có cùng tần số nhưng lệch pha nhau Hình 4.4.
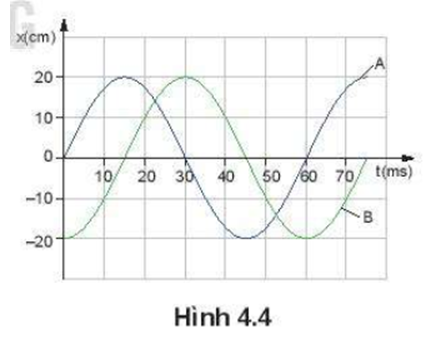
a) Xác định li độ dao động của vật B khi vật A có li độ cực đại và ngược lại.
b) Hãy cho biết vật A hay vật B đạt tới li độ cực đại trước.
c) Xác định độ lệch pha giữa dao động của vật A so với dao động của vật B.
Ở lớp 10, khi học về chuyển động của vật, ta đã biết có sự chuyển hoá giữa động năng và thế năng của vật. Vậy trong dao động điều hoà có sự chuyển hoá tương tự không?
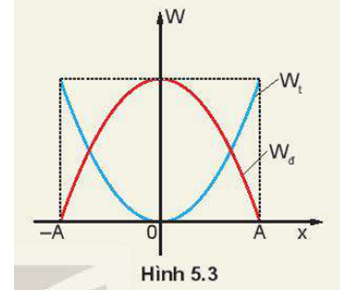
Hình 5.3 là đồ thị động năng và thế năng của một vật dao động điều hoà theo li độ. Hãy phân tích sự chuyển hoá giữa động năng và thế năng bằng đồ thị.
Hình 5.4 là đồ thị động năng và thế năng của một vật dao động điều hoà theo thời gian.
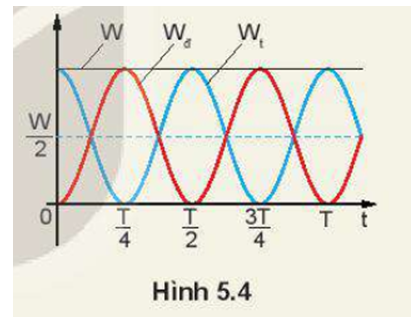
a) Động năng và thế năng của vật thay đổi như thế nào trong các khoảng thời gian: từ 0 đến , từ đến , từ đến , từ đến T.
b) Tại các thời điểm: , động năng và thế năng của vật có giá trị như thế nào (tính theo W). Nghiệm lại để thấy ở mỗi thời điểm đó Wđ + Wt = W.
Làm thí nghiệm để xác nhận rằng khi góc lệch thì chu kì của con lắc đơn gần như không phụ thuộc vào biên độ dao động.
Một con lắc lò xo có độ cứng k và vật nặng có khối lượng m.
1. Tính chu kì T.
2. Đo chu kì T bằng đồng hồ. So sánh hai kết quả thu được với kết quả tính ở Câu 1.
Một con lắc lò xo có vật nặng khối lượng 0,4 kg, dao động điều hoà. Đồ thị vận tốc v theo thời gian t như Hình 5.7.
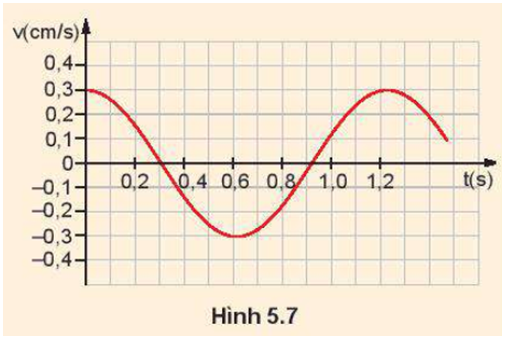
Tính:
a) Vận tốc cực đại của vật;
b) Động năng cực đại của vật;
c) Thế năng cực đại của con lắc;
d) Độ cứng k của lò xo.
Một con lắc lò xo gồm lò xo có độ cứng k = 100 N/m, vật nặng có khối lượng m = 200 g, dao động điều hoà với biên độ A = 5 cm.
a) Xác định li độ của vật tại thời điểm động năng của vật bằng 3 lần thế năng của con lắc.
b) Xác định tốc độ của vật khi vật qua vị trí cân bằng.
c) Xác định thế năng của con lắc khi vật có li độ x = -2,5 cm.
Phân tích sự chuyển hoá giữa động năng và thế năng trong dao động điều hoà ở một số ví dụ trong đời sống.
Đại lượng nào sau đây tăng gấp đôi khi biên độ của dao động điều hoà của con lắc lò xo tăng gấp đôi?
A. Cơ năng của con lắc.
B. Động năng của con lắc.
C. Vận tốc cực đại.
D. Thế năng của con lắc.Cơ năng của một chất điểm dao động điều hoà tỉ lệ thuận với
A. chu kì dao động.
B. biên độ dao động.
C. bình phương biên độ dao động.
D. bình phương chu kì dao động.
Trong dao động điều hoà thì tập hợp ba đại lượng nào sau đây không thay đổi theo thời gian?
A. Lực kéo về; vận tốc; năng lượng toàn phần.
B. Biên độ; tần số góc; gia tốc.
C. Động năng; tần số; lực kéo về.
D. Biên độ; tần số góc; năng lượng toàn phần.
Phương trình dao động điều hoà của một chất điểm dao động là: \(x = A{\rm{cos}}\left( {\omega t + \frac{{2\pi }}{3}} \right)\left( {{\rm{cm}}} \right)\). Biểu thức động năng của nó biến thiên theo thời gian là
A. \({W_d} = \frac{{m{A^2}{\omega ^2}}}{4}\left[ {1 + {\rm{cos}}\left( {2\omega t + \frac{\pi }{3}} \right)} \right]\).
B. \({W_{\rm{d}}} = \frac{{m{A^2}{\omega ^2}}}{4}\left[ {1 - {\rm{cos}}\left( {2\omega t + \frac{{4\pi }}{3}} \right)} \right]\).
C. \({W_d} = \frac{{m{A^2}{\omega ^2}}}{4}\left[ {1 + {\rm{cos}}\left( {2\omega t + \frac{{4\pi }}{3}} \right)} \right]\).
D. \({W_{\rm{d}}} = \frac{{m{A^2}{\omega ^2}}}{4}\left[ {1 - {\rm{cos}}\left( {2\omega t + \frac{\pi }{3}} \right)} \right]\).
Một chất điểm dao động điều hoà. Biết khoảng thời gian giữa năm lần liên tiếp động năng của chất điểm bằng thế năng của hệ là \(0,4{\rm{\;s}}\). Tần số của dao động của chất điểm là
A. \(2,5{\rm{\;Hz}}\).
B. \(3,125{\rm{\;Hz}}\).
C. \(5{\rm{\;Hz}}\).
D. \(6,25{\rm{\;Hz}}\).Một chất điểm có khối lượng m, dao động điều hoà với biên độ \({\rm{A}}\), tần số góc \(\omega \). Động năng cực đại của chất điểm là
A. \(\frac{{m{\omega ^2}{A^2}}}{2}\).
B. \(\frac{{{\omega ^2}{A^2}}}{{2m}}\).
C. \(\frac{{{\rm{mA}}{\omega ^2}}}{2}\).
D. \(\frac{{m\omega {A^2}}}{2}\).Một vật có khối lượng \({\rm{m}} = 0,4{\rm{\;kg}}\), dao động điều hoà với chu kì \({\rm{T}} = 0,2\pi \left( {\rm{s}} \right)\), biên độ bằng \(10{\rm{\;cm}}\). Tính cơ năng của dao động.
Một chất điểm có khối lượng \(100{\rm{\;g}}\) dao động điều hoà trên quỹ đạo là đoạn thẳng \({\rm{MN}}\) (dài hơn \(8{\rm{\;cm}}\)). Tại điểm \({\rm{P}}\) cách \({\rm{M}}\) một khoảng \(4{\rm{\;cm}}\) và tại điểm \({\rm{Q}}\) cách \({\rm{N}}\) một khoảng \(2{\rm{\;cm}}\), chất điểm có động năng tương ứng là \({32.10^{ - 3}}{\rm{\;J}}\) và \({18.10^{ - 3}}{\rm{\;J}}\). Tính tốc độ trung bình khi vật đi từ \({\rm{P}}\) đến \({\rm{Q}}\).
Một con lắc lò xo treo thẳng đứng vào điểm I cố định, quả cầu có khối lượng \(100{\rm{\;g}}\). Con lắc dao động điều hoà theo phương trình \({\rm{x}} = 4{\rm{cos}}10\sqrt {5{\rm{t}}} \left( {{\rm{cm}}} \right)\) với \({\rm{t}}\) tính theo giây. Lấy \({\rm{g}} = 10{\rm{\;m}}/{{\rm{s}}^2}\). Tính độ lớn lực đàn hồi lớn nhất và nhỏ nhất do lò xo tác dụng lên điểm I.
Một con lắc lò xo treo thẳng đứng. Biết rằng trong quá trình dao động, tỉ số giữa độ lớn lực đàn hồi lớn nhất và nhỏ nhất là \(\frac{7}{3}\), biên độ dao động là \(10{\rm{\;cm}}\). Lấy \({\rm{g}} = 10{\rm{\;m}}/{{\rm{s}}^2}\). Tính tần số dao động của vật.
Một con lắc đơn dao động điều hoà với biên độ góc \({\alpha _{{\rm{max}}}}\). Lấy mốc cơ năng tại vị trí cân bằng. Tính li độ góc của con lắc khi nó ở vị trí có động năng bằng thế năng.
Một con lắc lò xo gồm một lò xo nhẹ có độ cứng k, được treo thẳng đứng vào một giá cố định và một vật có khối lượng \(m = 100{\rm{\;g}}\). Khi vật ở vị trí cân bằng \({\rm{O}}\), lò xo dãn \(2,5{\rm{\;cm}}\). Kéo vật dọc theo trục của lò xo xuống dưới cách vị trí cân bằng \({\rm{O}}\) một đoạn \(2{\rm{\;cm}}\) rồi truyền cho nó vận tốc có độ lớn \(40\sqrt 3 {\rm{\;cm}}/{\rm{s}}\) theo phương thẳng đứng, hướng xuống dưới. Chọn trục toạ độ \({\rm{Ox}}\) theo phương thẳng đứng, gốc tại \({\rm{O}}\), chiều dương hướng lên trên, gốc thời gian là lúc vật bắt đầu dao động. Lấy \({\rm{g}} = 10{\rm{\;m}}/{{\rm{s}}^2}\). Biết chiều dài tự nhiên của của lò xo là \(50{\rm{\;cm}}\).
Tính độ cứng của lò xo, viết phương trình dao động và tính cơ năng dao động của vật.
Một con lắc lò xo gồm một lò xo nhẹ có độ cứng k, được treo thẳng đứng vào một giá cố định và một vật có khối lượng \(m = 100{\rm{\;g}}\). Khi vật ở vị trí cân bằng \({\rm{O}}\), lò xo dãn \(2,5{\rm{\;cm}}\). Kéo vật dọc theo trục của lò xo xuống dưới cách vị trí cân bằng \({\rm{O}}\) một đoạn \(2{\rm{\;cm}}\) rồi truyền cho nó vận tốc có độ lớn \(40\sqrt 3 {\rm{\;cm}}/{\rm{s}}\) theo phương thẳng đứng, hướng xuống dưới. Chọn trục toạ độ \({\rm{Ox}}\) theo phương thẳng đứng, gốc tại \({\rm{O}}\), chiều dương hướng lên trên, gốc thời gian là lúc vật bắt đầu dao động. Lấy \({\rm{g}} = 10{\rm{\;m}}/{{\rm{s}}^2}\). Biết chiều dài tự nhiên của của lò xo là \(50{\rm{\;cm}}\).
Xác định li độ và vận tốc của vật khi thế năng dao động bằng 1/3 động năng.
Một con lắc lò xo gồm một lò xo nhẹ có độ cứng k, được treo thẳng đứng vào một giá cố định và một vật có khối lượng \(m = 100{\rm{\;g}}\). Khi vật ở vị trí cân bằng \({\rm{O}}\), lò xo dãn \(2,5{\rm{\;cm}}\). Kéo vật dọc theo trục của lò xo xuống dưới cách vị trí cân bằng \({\rm{O}}\) một đoạn \(2{\rm{\;cm}}\) rồi truyền cho nó vận tốc có độ lớn \(40\sqrt 3 {\rm{\;cm}}/{\rm{s}}\) theo phương thẳng đứng, hướng xuống dưới. Chọn trục toạ độ \({\rm{Ox}}\) theo phương thẳng đứng, gốc tại \({\rm{O}}\), chiều dương hướng lên trên, gốc thời gian là lúc vật bắt đầu dao động. Lấy \({\rm{g}} = 10{\rm{\;m}}/{{\rm{s}}^2}\). Biết chiều dài tự nhiên của của lò xo là \(50{\rm{\;cm}}\).
Tính thế năng dao động, động năng và vận tốc của vật tại vị trí có li độ \(x = 2\sqrt 2 {\rm{cm}}\)
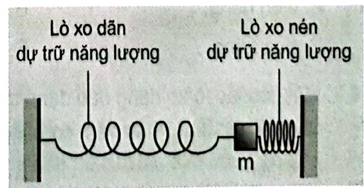
Hãy phân tích sự chuyển hoá năng lượng giữa động năng và thế năng trong hệ gồm hai lò xo và vật nặng \({\rm{m}}\) được mắc như Hình 5.1. khi quả nặng được thả cho dao động.
Một người khối lượng \(83{\rm{\;kg}}\) treo mình vào sợi dây bungee đàn hồi có độ cứng \({\rm{k}} = 270{\rm{\;N}}/{\rm{m}}\) (Hình 5.2). Từ vị trí cân bằng, người này được kéo đến vị trí mà sợi dây dãn \(5{\rm{\;m}}\) so với chiều dài tự nhiên rồi thả ra. Coi chuyển động của người đó là một dao động điều hoà. Xác định vị trí và vận tốc của người này sau \(2{\rm{\;s}}\). Lấy \({\rm{g}} = 9,8{\rm{\;m}}/{{\rm{s}}^2}\).

Ta có thể sử dụng định luật bảo toàn cơ năng để tìm li độ và vận tốc của vật dao động điều hoà được không?
Hình 7.3 mô tả một máy đo địa chấn đơn giản hoạt động theo nguyên tắc sau đây: Khi xảy ra động đất thì hệ gồm lò xo và vật nặng của máy đo sẽ dao động theo tần số của địa chấn. Bút dạ gắn với vật nặng sẽ ghi lại đồ thị của địa chấn trên cuộn giấy quay đều. Biết sóng địa chấn có tần số nằm trong khoảng từ 30 Hz đến 40 Hz.
Hãy giải thích tại sao tần số riêng của hệ (vật nặng + lò xo) trong máy địa chấn phải có giá trị nhỏ hơn tần số này rất nhiều.

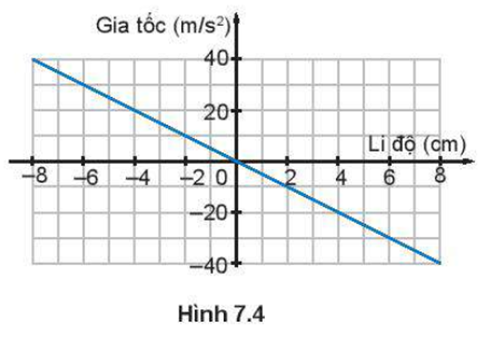
Đồ thị Hình 7.4 mô tả mối liên hệ giữa gia tốc và li độ của một vật dao động điều hoà.
Sử dụng số liệu trong đồ thị Hình 7.4 để tính tần số của dao động.
Hình 7.5 là đồ thị động năng theo thời gian của một vật khối lượng 0,4 kg dao động điều hoà. Tại thời điểm ban đầu vật đang chuyển động theo chiều dương, lấy 2 = 10. Viết phương trình dao động của vật.
Một vật có khối lượng m dao động điều hoà với tần số góc và biên độ A.
a) Khi vật có li độ bằng một nửa biên độ thì động năng và thế năng chiếm bao nhiêu phần trăm so với cơ năng?
b) Tại li độ nào thì thế năng bằng động năng?
Phân tích được sự chuyển hóa năng lượng trong dao động điều hòa trong một số bài tập cụ thể.
- (A) ω.
- (B) cos(ωt + φ).
- (C) (ωt + φ).
- (D) φ.
Một vật dao động điều hòa với biên độ bằng 4 cm. Khi pha của dao động bằng thì li độ của vật bằng:
- (A) 2 cm.
- (B) 4 cm.
- (C) - 2 cm.
- (D) - 4 cm.
Trong dao động điều hòa, giá trị cực đại của vận tốc là
- (A) vmax = ω
- (B) vmax = ω2
- (C) vmax = - ω
- (D) v max = - ω2
Một chất điểm dao động điều hòa có phương trình vận tốc là (cm/s). Gốc tọa độ ở vị trí cân bằng. Mốc thời gian được Đáp án đúng là vào lúc chất điểm có li độ và vận tốc là:
- (A) x = 2cm, v = 0.
- (B) x = 0, v = 3π cm/s.
- (C) x= − 2 cm, v = 0.
- (D) x = 0, v = − π cm/s.
Gia tốc của một chất điểm dao động điều hòa biến thiên
- (A) cùng tần số và cùng pha với li độ.
- (B) cùng tần số và ngược pha với li độ.
- (C) khác tần số và vuông pha với li độ.
- (D) khác tần số và cùng pha với li độ.
Một vật nhỏ dao động điều hòa theo một quỹ đạo có chiều dài 10 cm. Biên độ của dao động là
- (A) 10 cm.
- (B) 5 cm.
- (C) 2,5 cm.
- (D) 1,125 cm.
Một vật dao động điều hòa với tần số góc bằng trên quỹ đạo dài 8 cm. Biết pha ban đầu của dao động là Li độ của vật ở thời điểm t = 0,25 s kể từ lúc bắt đầu dao động có giá trị bằng:
- (A)
- (B)
- (C)
- (D)
Một quả cầu dao động điều hoà với biên độ 5 (cm), chu kỳ 0,4 (s). Tính vận tốc cùa quả cầu tại thời điểm vật có li độ 3 (cm) và đang chuyển động theo chiều dương.
- (A) v = 62,8 (cm/s)
- (B) v = ± 62,8 (cm/s)
- (C) v = − 62,8 (cm/s).
- (D) v = 62,8 (m/s).
Một vật dao động theo phương trình (t đo bằng giây). Tại thời điểm t1 li độ là cm và đang giảm. Tính li độ sau thời điểm t1 là 3 (s).
- (A) 1,2 cm.
- (B) -3 cm.
- (C) -2 cm.
- (D) 5 cm.
Cho một chất điểm M chuyển động tròn đều trên đường tròn có bán kính bằng 8 cm với vận tốc góc bằng 300 vòng/phút. Gọi P là hình chiếu của M xuống một đường thẳng nằm trong mặt phẳng quỹ đạo. Biên độ và chu kì dao động của điểm P tương ứng là
- (A) 4 cm; 10 s.
- (B) 8 cm; 10 s.
- (C) 8 cm; 0,2 s.
- (D) 8 cm; 0,2 s.
Một vật dao động với phương trình x = 5cos(4πt + ) cm. Tại thời điểm t = 1 s hãy xác định li độ của dao động.
- (A) 2,5 cm.
- (B) 5 cm.
- (C) cm.
- (D) cm.
Một vật dao động điều hoà, trong thời gian 1 phút vật thực hiện được 30 dao động. Chu kì dao động của vật là
- (A) 2 s.
- (B) 0,5 s.
- (C) 1 s.
- (D) 30 s.
- (A) m2 = 0,1 kg.
- (B) m2 = 0,3 kg.
- (C) m2 = 8,1 kg.
- (D) m2 = 2,7 kg.
Con lắc lò xo gồm lò xo k và vật m, dao động điều hòa với tần số f = 1,5 Hz. Muốn tần số dao động của con lắc là Hz thì khối lượng của vật m' phải là
- (A) m' = 2m
- (B) m' = 3m
- (C) m' = 4m
- (D) m' = 5m
Trong dao động điều hòa của một con lắc lò xo, nếu giảm khối lượng của vật nặng đi 4 lần thì chu kì của con lắc lò xo sẽ
- (A) tăng 4 lần.
- (B) tăng 16 lần.
- (C) giảm 2 lần.
- (D) giảm 16 lần.
Một con lắc lò xo có vật nặng 400 gam dao động điều hòa. Vật thực hiện được 50 dao động trong thời gian 20 s. Lấy Độ cứng của lò xo là
- (A) 50 N/ m.
- (B) 100 N/ m.
- (C) 150 N/ m.
- (D) 200 N/ m.
Một con lắc lò xo gồm lò xo có độ cứng k = 20 N/ m và vật nhỏ có khối lượng m = 0,2 kg. Khi vật dao động điều hòa, tại thời điểm t, vận tốc và gia tốc của vật lần lượt là 20 cm/s và Biên độ dao động của vật là
- (A) 4 cm.
- (B) cm.
- (C) cm.
- (D) 8 cm.
Một con lắc lò xo đang dao động điều hòa theo phương ngang với biên độVật nhỏ của con lắc có khối lượng 100 gam lò xo có độ cứng 100N/m. Khi vật nhỏ có vận tốc thì gia tốc của nó có độ lớn là
- (A)
- (B)
- (C)
- (D)
Một con lắc lò xo gồm lò xo có khối lượng không đáng kể, có độ cứng k = 100 N/m, khối lượng của vật nặng m = 1 kg. Kéo vật khỏi vị trí cân bằng x = 3 cm và truyền cho vật vận tốc v = 30 cm/s theo chiều dương. Chọn t = 0 là lúc vật bắt đầu chuyển động. Phương trình dao động của vật là
- (A)
- (B)
- (C)
- (D)
Một con lắc đơn có chiều dài 121 cm dao động điều hòa tại nơi có gia tốc trọng trường g. Lấy Chu kì dao động của con lắc là
- (A) 0,5 s.
- (B) 2 s.
- (C) 1 s.
- (D) 2,2 s.
Tại nơi có gia tốc trọng trường g = 9,8 m/s, một con lắc đơn và một con lắc lò xo nằm ngang dao động điều hòa với cùng tần số. Biết con lắc đơn có chiều dài 49 cm và lò xo có độ cứng 10 N/m. Khối lượng vật nhỏ của con lắc lò xo là
- (A) 0,125 kg.
- (B) 0,500 kg.
- (C) 0,750 kg.
- (D) 0,250 kg.
Một con lắc đơn có chiều dài l = 64 cm dao động điều hòa tại một nơi có gia tốc trọng trường là Con lắc thực hiện được bao nhiêu dao động trong thời gian là 12 phút?
- (A) 250.
- (B) 400.
- (C) 500.
- (D) 450.
Một con lắc đơn có chu kỳ dao động điều hòa là T. Khi giảm chiều dài con lắc 10 cm thì chu kỳ dao động của con lắc biến thiên 0,1 s. Chu kỳ dao động T ban đầu của con lắc là
- (A) T = 1,9 s.
- (B) T = 1,95 s.
- (C) T = 2,05 s.
- (D) T = 2 s.
Hai con lắc đơn có chiều dài hơn kém nhau 222cm đặt ở cùng một nơi. Người ta thấy rằng trong cùng một khoảng thời gian con lắc thứ nhất thực hiện được 30 dao động, con lắc thứ hai được 36 dao động. Chiều dài của các con lắc là
- (A) 72 cm và 50 cm
- (B) 50 cm và 70 cm
- (C) 44 cm và 22 cm
- (D) 132 cm và 110 cm
Vật dao động điều hòa theo một trục cố định (mốc thế năng ở vị trí cân bằng) thì
- (A) động năng của vật cực đại khi gia tốc của vật có độ lớn cực đại.
- (B) khi vật đi từ vị trí cân bằng ra biên thì vận tốc và gia tốc luôn cùng dấu.
- (C) khi ở vị trí cân bằng, thế năng của vật bằng cơ năng.
- (D) thế năng của vật cực đại khi vật ở vị trí biên.
- (A)
- (B)
- (C)
- (D)
Con lắc lò xo nằm ngang có dao động điều hoà. Khi vật có động năng thì cách vị trí cân bằng 1 cm khi có động năng thì cách vị trí cân bằng một đoạn là
- (A)
- (B) 2 cm
- (C)
- (D)
Một con lắc lò xo có độ cứng và có năng lượng dao động là Biên độ dao động của nó là
- (A) 2 cm
- (B) 0,4 cm
- (C) 0,04 cm
- (D) 4 mm
Con lắc lò xo gồm vật nhỏ khối lượng và lò xo có độ cứng k. Kích thích cho vật dao động điều hoà với cơ năng . Khi vật qua vị trí có li độ thì vật có vật tốc Độ cứng kk của lò xo bằng
- (A) 250 N/m
- (B) 200 N/m
- (C) 150 N/m
- (D) 100 N/m
Một con lắc lò xo đặt nằm ngang gồm vật nặng khối lượng 1kg và lò xo khối lượng không đáng kể có độ cứng 100 N/m dao động điều hoà. Trong quá trình dao động chiều dài của lò xo biến thiên từ 20 cm đến 32 cm. Cơ năng của con lắc bằng
- (A) 3J
- (B) 1,5J
- (C) 0,36J
- (D) 0,18J
Một vật nặng 500 g dao động điều hoà trên quỹ đạo dài 20 cm và trong khoảng thời gian 3 phút vật thực hiện 540 dao động. Cho Cơ năng của vật khi dao động là
- (A) 2025J
- (B) 0,9J
- (C) 2,025J
- (D) 900J
Một vật dao động điều hòa dọc theo trục Ox. Mốc thế năng ở vị trí cân bằng, ở thời điểm độ lớn vận tốc của vật bằng 50% vận tốc cực đại thì tỉ số giữa động năng và cơ năng của vật là
- (A) 3/4.
- (B) 1/4.
- (C) 4/3.
- (D) 1/2
Một vật dao động điều hòa với biên độ 6 cm. Mốc thế năng ở vị trí cân bằng. Khi vật có động năng bằng 3/4 lần cơ năng thì vật cách vị trí cân bằng một đoạn.
- (A) 6 cm.
- (B) 4,5 cm.
- (C) 4 cm.
- (D) 3 cm.
Một con lắc lò xo gồm lò xo nhẹ và vật nhỏ dao động điều hòa theo phương ngang với tần số góc 10 rad/s. Biết rằng khi động năng và thế năng (mốc ở vị trí cân bằng của vật) bằng nhau thì vận tốc của vật có độ lớn bằng 0,6 m/s. Biên dộ dao của con lắc là
- (A) 6cm.
- (B) 6cm
- (C) 12 cm.
- (D) cm.
Một con lắc lò xo gồm quả cầu nhỏ khối lượng 1 kg và lò xo có độ cứng 50 N/m. Cho con lắc dao động điều hòa trên phương nằm ngang. Tại thời điểm vận tốc của quả cầu là 0,2 m/s thì gia tốc của nó là − m/s2. Cơ năng của con lắc là
- (A) 0,02 J.
- (B) 0,05 J.
- (C) 0,04 J.
- (D) 0,01 J.
Một con lắc lò xo gồm vật nặng 0,2 kg gắn vào đầu lò xo có độ cứng 20 N/m. Kéo quả nặng ra khỏi vị trí cân bằng rồi thả nhẹ cho nó dao động, tốc độ trung bình trong 1 chu kỳ là 160/π cm/s. Cơ năng dao dao động của con lắc là
- (A) 320 J.
- (B) 6,4.10−2J.
- (C) 3,2.10−2J.
- (D) 3,2 J.
Hằng ngày, chúng ta thấy rất nhiều chuyển động, trong đó, vật chuyển động qua lại quanh một vị trí cân bằng. Chuyển động của người chơi đu là một ví dụ như vậy (Hình 1.1).

Những chuyển động đó được gọi là dao động. Mô tả dao động như thế nào?
Dùng một lò xo, một quả cầu nhỏ bằng kim loại, sợi dây và giá thí nghiệm, thảo luận với bạn xây dựng phương án và thực hiện phương án tạo ra dao động của quả cầu treo ở một đầu lò xo.
Dụng cụ
Quả cầu kim loại nhỏ, sợi dây mảnh nhẹ, giá thí nghiệm.
Tiến hành
+ Treo quả cầu vào giá thí nghiệm.
+ Khi quả cầu đứng yên tại vị trí cân bằng, dây treo có phương thẳng đứng, kéo quả cầu khỏi vị trí cân bằng một đoạn nhỏ rồi buông tay cho quả cầu chuyển động (Hình 1.2).
+ Mô tả chuyển động của quả cầu.