Processing math: 100%

Một chất điểm có khối lượng 100g dao động điều hoà trên quỹ đạo là đoạn thẳng MN (dài hơn 8cm ). Tại điểm

TẢI VỀ (.doc)
Để download Câu trắc nghiệm này dạng file WORDS (.doc) các bạn click vào nút TẢI VỀ bên trên.

Câu hỏi

🗣️ Trần Thị Phát hỏi: Cho mình hỏi một câu Vật lý Lớp 11 trong sách bài tập Sách Kết Nối Tri Thức

Một chất điểm có khối lượng 100g dao động điều hoà trên quỹ đạo là đoạn thẳng MN (dài hơn 8cm). Tại điểm P cách M một khoảng 4cm và tại điểm Q cách N một khoảng 2cm, chất điểm có động năng tương ứng là 32.10−3J và 18.10−3J. Tính tốc độ trung bình khi vật đi từ P đến Q.

👩 Đánh giá của giáo viên: Câu này dễ, mức độ biết.

🔑 Chủ đề: giai sbt vat ly 11 kntt su chuyen hoa nang luong trong dao dong dieu hoa co dap an.

Câu trả lời hay nhất

🕵 Bạn Nguyễn Khôi Minh trả lời:

Tốc độ tại P: vP=√2WdPm=80cm/s ; tại Q: vQ=√2WdQm=60cm/s . Do vP>vQ nên li độ |xP|<|xQ|:{|xP|=A−4|xQ|=A−2 {v2P=ω2(A2−x2P)v2Q=ω2(A2−x2Q)⇒{v2P=8ω2(A−2)v2Q=4ω2(A−1) Giải hệ ta được: A=10cm và ω=10rad/s . Quãng đường PQ=OP+OQ=(A−4)+(A−2)=14cm. Thời gian vật đi từ P đến Q là Δt với: Δt=Δφω . Δφ=π−(φ1+φ2)=π2 , với cosφ1=OPA;cosφ2=OQA⇒Δt=T4=π20 ⇒ Tốc độ trung bình khi vật đi từ P đến Q: ¯v=PQΔt=14π20≈89cm/s .

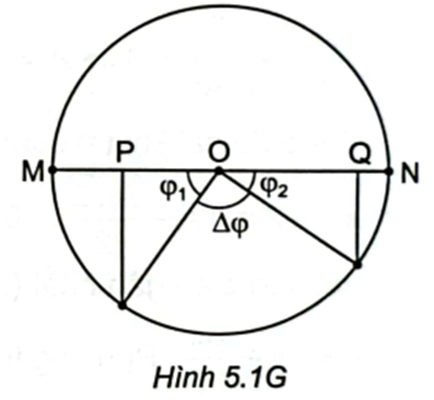
Tốc độ tại P: \({v_P} = \sqrt {\frac{{2{W_{dP}}}}{m}} = 80{\rm{\;cm/s}}\) ; tại Q: \({v_Q} = \sqrt {\frac{{2{W_{dQ}}}}{m}} = 60{\rm{\;cm/s}}\) . Do \({v_P} > {v_Q}\) nên li độ \(\left| {{x_P}} \right| < \left| {{x_Q}} \right|:\left\{ {\begin{array}{*{20}{l}}{\left| {{x_P}} \right| = A - 4}\\{\left| {{x_Q}} \right| = A - 2}\end{array}} \right.\) \(\left\{ {\begin{array}{*{20}{l}}{v_P^2 = {\omega ^2}\left( {{A^2} - x_P^2} \right)}\\{v_Q^2 = {\omega ^2}\left( {{A^2} - x_Q^2} \right)}\end{array} \Rightarrow \left\{ {\begin{array}{*{20}{l}}{v_P^2 = 8{\omega ^2}\left( {A - 2} \right)}\\{v_Q^2 = 4{\omega ^2}\left( {A - 1} \right)}\end{array}} \right.} \right.\) Giải hệ ta được: \(A = 10{\rm{\;cm}}\) và \(\omega = 10{\rm{rad}}/{\rm{s}}\) . Quãng đường \(PQ = OP + OQ\)\( = \left( {A - 4} \right) + \left( {A - 2} \right) = 14{\rm{\;cm}}{\rm{.\;}}\) Thời gian vật đi từ P đến Q là \({\rm{\Delta }}t\) với: \({\rm{\Delta }}t = \frac{{{\rm{\Delta }}\varphi }}{\omega }\) . \({\rm{\Delta }}\varphi = \pi - \left( {{\varphi _1} + {\varphi _2}} \right) = \frac{\pi }{2}\) , với \({\rm{cos}}{\varphi _1} = \frac{{{\rm{OP}}}}{{\rm{A}}};{\rm{cos}}{\varphi _2} = \frac{{{\rm{OQ}}}}{{\rm{A}}} \Rightarrow {\rm{\Delta t}} = \frac{{\rm{T}}}{4} = \frac{\pi }{{20}}\) \( \Rightarrow \) Tốc độ trung bình khi vật đi từ P đến Q: \(\overline v = \frac{{PQ}}{{{\rm{\Delta }}t}} = \frac{{14}}{{\frac{\pi }{{20}}}} \approx 89{\rm{\;cm/s}}\) .

Câu trước | Câu kế tiếp

Gửi bạn các file hữu ích đi kèm câu hỏi:

Sách - Tổng hợp Toán Tuổi Thơ - Năm 2016 - Trung học cơ sở
Sách - Tổng hợp Toán Tuổi Thơ - Năm 2016 - Trung học cơ sở
Sách - Tổng ôn cấp tốc môn Toán học ôn thi THPTQG | Sach ID
Sách - Tổng ôn cấp tốc môn Toán học ôn thi THPTQG | Sach ID

Làm thêm Vật lý Lớp 11

Trong một cửa hàng, cửa ra vào được thiết kế đóng tự động nhờ một hệ thống lò xo bên trong bản lề. Sau khi khách hàng mở cửa và ngừng tác dụng lực, cánh
Trong một cửa hàng, cửa ra vào được thiết kế đóng tự động nhờ một hệ thống lò xo bên trong bản lề. Sau khi khách hàng mở cửa và ngừng tác dụng lực, cánh
Chuẩn bị - Giá thí nghiệm. - Dây đàn hồi PQ. - Bộ rung. - Máy phát tần số. Tiến hành Bố trí thí nghiệm như Hình 13.1. Bước 1: Giữ cho dây căng,
Chuẩn bị - Giá thí nghiệm. - Dây đàn hồi PQ. - Bộ rung. - Máy phát tần số. Tiến hành Bố trí thí nghiệm như Hình 13.1. Bước 1: Giữ cho dây căng,
Hình 7P.1 mô tả các hiện tượng xảy ra đối với sóng vô tuyến có các tần số khác nhau do tác dụng của tầng điện li ở khí quyển. a) Gọi tên các hiện tượng
Hình 7P.1 mô tả các hiện tượng xảy ra đối với sóng vô tuyến có các tần số khác nhau do tác dụng của tầng điện li ở khí quyển. a) Gọi tên các hiện tượng
So sánh chức năng của mạch tách sóng và loa trong máy thu sóng với mạch trộn sóng và micro trong máy phát sóng.
So sánh chức năng của mạch tách sóng và loa trong máy thu sóng với mạch trộn sóng và micro trong máy phát sóng.
Trong một thí nghiệm Y-âng, biết a = 0,15 mm, D = 1,20 m, khoảng cách giữa 12 vân sáng liên tiếp là 5,2 mm. Tính bước sóng ánh sáng.
Trong một thí nghiệm Y-âng, biết a = 0,15 mm, D = 1,20 m, khoảng cách giữa 12 vân sáng liên tiếp là 5,2 mm. Tính bước sóng ánh sáng.
Hãy biểu diễn các miền bức xạ trong Bảng 2.2 theo bậc độ lớn bước sóng của chúng trên cùng một thang đo.
Hãy biểu diễn các miền bức xạ trong Bảng 2.2 theo bậc độ lớn bước sóng của chúng trên cùng một thang đo.