Vượt quá đường chân trời
Nghiệm Schwarzschild của các phương trình Einstein phát biểu rằng khi một vật khối lượng đủ lớn co lại dưới sức nặng của riêng nó, nó sẽ đạt tới một kích cỡ tới hạn mà vượt quá sẽ không có cái gì làm nó ngừng co lại nữa, cho dù vật bị nén lại bao nhiêu. Đây là kích cỡ mà theo lực hấp dẫn Newton và tính toán của Michell ngôi sao phải có để cho vận tốc thoát bằng tốc độ ánh sáng. Nhưng có một sự khác biệt chính trong thuyết tương đối.
Nếu chúng ta chỉ sử dụng các quy tắc của lực hấp dẫn Newton thì, biết áp suất nội tại của ngôi sao co lại là đủ mạnh, thì chẳng có lí do gì tại sao nó không ngừng co lại ngay tại, hay vừa vượt qua, kích cỡ tới hạn này. Nó chỉ phụ thuộc vào tình trạng tại đó các phân tử, nguyên tử hay thậm chí các hạt hạ nguyên tử nói đủ là đủ, nên chúng ta sẽ không chịu thêm bất kì sự nén nào nữa.
Lực hấp dẫn theo Newton phát triển theo cái trong toán học gọi là mối liên hệ nghịch đảo bình phương theo khoảng cách. Điều này có nghĩa là nếu một ngôi sao co lại đến một kích cỡ có bán kính bằng một nửa giá trị ban đầu của nó thì lực hấp dẫn trên bề mặt của nó sẽ mạnh gấp bốn lần. Nếu nó co lại bằng một phần ba bán kính ban đầu của nó thì lực hấp dẫn sẽ mạnh gấp chín lần, nếu nó co lại bằng một phần tư thì lực tăng gấp mười sáu lần, và cứ thế. Khi bán kính nhỏ dần thì lực hấp dẫn mạnh dần. Nếu có khả năng cho toàn bộ khối lượng của ngôi sao nén lại vào một điểm kích cỡ zero (lúc này nó có bán kính bằng zero) thì lực hấp dẫn sẽ là vô hạn.
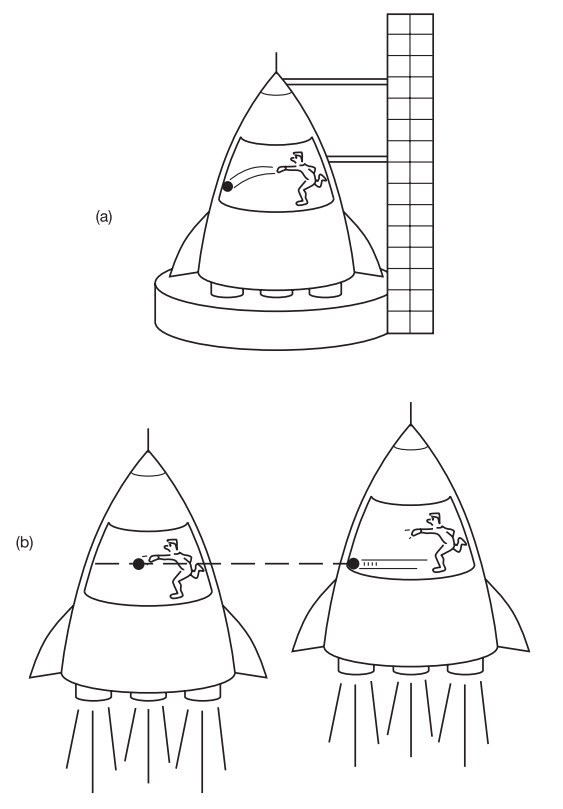
Thuyết tương đối tổng quát trình bày về những cái khác hoàn toàn. Nếu một ngôi sao co đến một kích cỡ tới hạn nào đó, sao cho vận tốc thoát của nó bằng tốc độ ánh sáng, thì lực hấp dẫn trên bề mặt của nó sẽ là vô hạn! Ở đây tôi muốn nói lực cần thiết để làm nó ngừng co lại thêm sẽ là vô hạn. Bán kính của kích cỡ tới hạn này được gọi là bán kính Schwarzschild và đánh dấu ranh giới của một lỗ đen. Ngày nay chúng ta thấy rằng sự co lại phải tiếp tục vượt quá bán kính này. Nếu bạn nghiêng về toán học2, bạn có thể tự hỏi3 làm thế nào lực này là vô hạn ở bán kính Schwarzschild và còn mạnh hơn nữa sau khi ngôi sao co lại thêm. Làm thế nào có cái gì đó còn lớn hơn vô hạn?! Câu trả lời nằm ở phần thảo luận (trong Chương 2) nói về những vật rơi tự do. Hãy nhớ lại rằng khi bạn đang rơi tự do, thí dụ tại cuối đầu dây thả từ trên máy bay (và trước khi bạn chạm đất), gia tốc của bạn triệt tiêu tác dụng của lực hấp dẫn nên bạn chẳng cảm thấy lực hút hấp dẫn nào cả. Tương tự như vậy, khi bề mặt của ngôi sao co lại qua bán kính tới hạn của nó thì bề mặt của nó không chịu lực hút hấp dẫn nào của phần bên trong của ngôi sao. Đây là lí do ngôi sao không thể ngừng co ở bán kính tới hạn đó vì lúc này không thể làm nó ngừng co lại thêm nữa.
Bên trong bán kính Schwarzschild, không có gì – ngay cả ánh sáng – có thể thoát ra ngoài. Hãy tưởng tượng một quả cầu có bán kính bằng bán kính Schwarzchild và bao xung quanh ngôi sao đã co lại. Một mặt cầu tưởng tượng như thế được gọi là chân trời sự kiện và là ranh giới nhân tạo trong không gian đánh dấu điểm không phản hồi. Bên ngoài chân trời đó, lực hấp dẫn mạnh nhưng là hữu hạn và có khả năng cho các vật thoát khỏi sức hút của nó. Nhưng một khi ở bên trong chân trời đó, một vật sẽ cần phải chuyển động nhanh hơn ánh sáng mới thoát ra, và điều này là không được phép. Như vậy, chân trời sự kiện là một khái niệm hơi khó chịu ở chỗ nó cho phép sự thông lưu có một chiều.
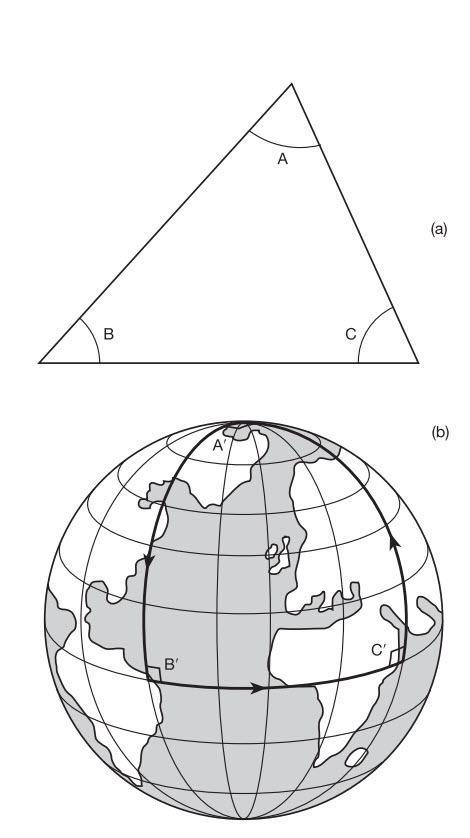
Chân trời sự kiện là một tên gọi thích hợp vì nó có thể sánh (đại khái) với ý nghĩa chung của từ “chân trời” trên Trái đất. Đây là đường nhân tạo đánh dấu khoảng cách xa nhất mà ta có thể nhìn thấy và là nơi mặt đất tiếp giáp với bầu trời. Chúng ta hiểu ranh giới này là do sự cong của Trái đất và, vì ánh sáng truyền đi ít nhiều theo đường thẳng ở gần mặt đất, nên chúng ta không thể nhìn thấy bên ngoài đường chân trời. Theo kiểu giống như vậy, chân trời của một lỗ đen đánh dấu ranh giới mà vượt qua đó chúng ta không thể nhìn thấy bất kì “sự kiện” nào. Nhưng không giống như đường chân trời trên Trái đất liên tục di chuyển khi chúng ta tiến về phía nó, chân trời sự kiện là cố định và chúng ta có thể đến gần nó như chúng ta muốn, và thậm chí đi vượt qua nó nếu chúng ta có đủ xuẩn ngốc để làm như vậy.
Tất cả các vật thể đều có chân trời sự kiện tiềm tàng của riêng nó với bán kính Schwarschild của riêng nó. Ngay cả Trái đất cũng có thể làm thành một lỗ đen, nhưng vì nó không có đủ khối lượng để tự co lại nên nó sẽ phải bị nén từ bên ngoài. Đừng hỏi tôi làm sao mà nén, tôi chỉ nói rằng nếu nó có thể bị nén đủ chặt thì cuối cùng nó sẽ vượt qua chân trời sự kiện của riêng nó, lúc đó sự co lại của nó sẽ tự duy trì. Bán kính Schwarzschild của Trái đất nhỏ hơn nửa centi mét, tức là bất kì lỗ đen nào có chứa vật chất bằng hành tinh của chúng ta sẽ có kích cỡ chừng bằng hạt đậu.
Một khi một ngôi sao co lại đã bị nén qua chân trời sự kiện của nó, thì không có gì có thể ngăn cản nó tiếp tục co lại thêm cho tới khi toàn bộ khối lượng của nó bị ép xuống còn một điểm. Điểm này gọi là điểm kì dị và thật sự là một thực thể rất kì lạ. Nó lạ đến mức trên thực tế các định luật vật lí hoạt động – trong chừng mực mà chúng ta biết – hoàn hảo ở mọi nơi, mô tả hành trạng của những hạ nguyên tử nhỏ bé nhất đến tính chất của Vũ trụ tổng thể, cũng bị phá vỡ tại điểm kì dị của một lỗ đen. Vì thế, đối với Vũ trụ bên ngoài thì chân trời sự kiện đã che chắn chúng ta thoát khỏi sự quái dị như thế.
Không có chân trời sự kiện, ai biết được điểm kì dị sửa lại các định luật vật lí bên ngoài lỗ đen như thế nào. Thật vậy, chân trời sự kiện quá quan trọng nên các nhà vật lí đã phát minh ra định luật kiểm duyệt vũ trụ nghe có vẻ to tát mà họ hi vọng sẽ áp dụng được ở mọi nơi trong tự nhiên. Chúng tác dụng giống như Mary Whitehouse4 của vũ trụ học bảo vệ Vũ trụ chống lại sự hỗn độn, sự mất khả năng dự đoán và các vô hạn của điểm kì dị. Vậy định luật này phát biểu ra sao? Đơn giản thôi: “Mi sẽ không có những điểm kì dị trần”. Bạn nên nhớ rằng phát biểu hài hước này thật ra chỉ là một giả thuyết và hóa ra khá tốt, ít nhất là trong những kịch bản nhất định, chứ không luôn luôn như vậy. Chẳng hạn, nó khẳng định rằng những lỗ đen nhỏ xíu, nhỏ hơn các nguyên tử, có lẽ đã được tạo ra ngay sau Big Bang và từ từ bay hơi qua một quá trình gọi là bức xạ Hawking (cái chúng ta sẽ gặp ở phần cuối chương). Một số phép tính cho thấy cái có thể còn lại ở cuối quá trình bay hơi này là những điểm kì dị trần. Tuy nhiên, kết quả này vẫn còn mơ hồ.
Theo các phương trình của thuyết tương đối tổng quát, điểm kì dị là nơi vật chất có mật độ vô hạn, không gian cong vô hạn và thời gian đi đến kết thúc. Có một sự hiểu sai thường gặp là thời gian đi tới kết thúc tại chân trời sự kiện. Đây là vì cái những người quan sát ở xa nhìn thấy khi họ đang nhìn cái gì đó rơi vào trong lỗ đen. Tôi sẽ nói tới vấn đề này ở phần sau; còn ở đây tôi muốn trở lại với điểm kì dị đánh dấu sự kết thúc của thời gian.
Rung chuông khoa trương ư? Việc phải làm thôi. Đây chính là cách tôi đã mô tả bản thân Big Bang. Chỉ có điều Big Bang đánh dấu sự ra đời chứ không phải sự kết thúc của thời gian. Ngoại trừ hai trường hợp giống đáng kể với Big Bang là mẹ đẻ của mọi điểm kì dị; một điểm kì dị trần hiện ra.
Trở lại với lỗ đen và cái bên trong chúng mà khi xác định bởi chân trời sự kiện là không gian hoàn toàn trống rỗng, trừ điểm kì dị tại tâm của nó (và trừ bất kì phần vật chất nào đã bị lỗ đen bắt giữ và rơi vào). Lí do khiến điểm kì dị có mật độ vô hạn có thể được xem xét là nếu chúng ta xét cách chúng ta tính mật độ của một vật. Đó là tỉ số của khối lượng của nó và kích cỡ của nó. Như vậy, nếu một vật có khối lượng bất kì có kích cỡ zero thì để thu được mật độ của nó ta phải chia một số khác không cho số không. Và, hãy tin tôi, đây là cái không ai muốn làm trong toán học. Bạn hãy tự mình thử đi. Chia một số bất kì cho số không trên máy tính bỏ túi. Máy tính của tôi cho tôi kí hiệu “-E-” kí hiệu cho “error” (sai) vì một cái máy tính nhỏ không thể xử lí phép tính vô hạn. Ngay cả máy tính trạm công suất mạnh của tôi mà tôi dùng trong nghiên cứu tại trường đại học cũng không xài được. Nếu nó gặp một phép chia cho số không thì chương trình đang chạy bị hỏng. Ít nhất thì nó cung cấp cho tôi một câu thông báo tình trạng trục trặc dưới dạng mã hóa. Tuy nhiên, hóa ra điểm kì dị không hẳn đáng sợ như thế này. Khi chúng ta áp dụng các quy tắc của cơ học lượng tử, như chúng ta phải làm ở thang bậc này, chúng ta phát hiện thấy điểm kì dị có kích cỡ cực kì nhỏ (nhỏ hơn nhiều so với một nguyên tử) nhưng khác không. Nhiều chi tiết vật lí chưa được làm sáng tỏ, vì việc áp dụng các quy tắc của cơ học lượng tử đồng thời với các quy tắc của thuyết tương đối tổng quát là cái chưa có ai biết làm thế nào cho thích hợp.
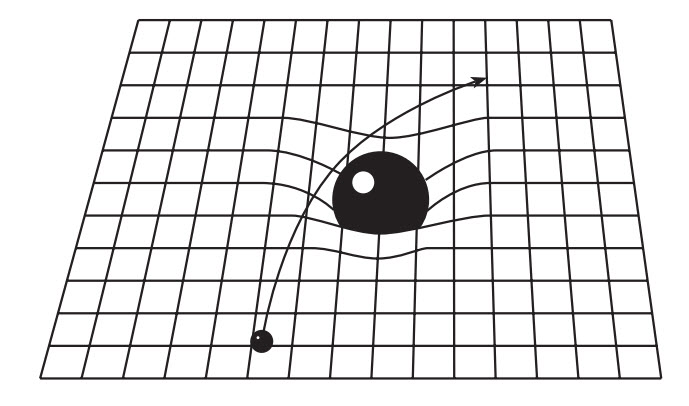
Vì thế, một cái lỗ đen là rất đơn giản về cấu trúc của nó. Nó có một cái tâm (điểm kì dị) và một mặt (chân trời sự kiện). Tất cả những cái khác là sự hấp dẫn. Tất nhiên, cái làm cho lỗ đen thú vị như thế là cách thức lực hấp dẫn cực lớn của chúng ảnh hưởng đến không gian (và thời gian5) xung quanh.
Lỗ đen, lỗ sâu đục và cỗ máy thời gian
Jim Al-Khalili
Bản dịch của Thuvienvatly.com
___
2Đừng lo nếu bạn không hiểu nhiều về toán học
3Đừng lo nếu bạn thiên về toán học mà không tự hỏi điều gì!
4Mary Whitehouse là thư kí danh dự của Hội Nghe Nhìn Quốc gia ở Anh và đã lên chiến dịch trong nhiều năm nhằm “quét sạch” các phương tiện này và những phương tiện khác bằng cách hồi phục lại một quan điểm tình dục “cân bằng” hơn trong các chương trình xem trong nhà.
5Những người say mê thuyết tương đối và lỗ đen có lẽ đang hỏi tại sao tôi lại tránh nói tới thời gian và cách thức nó bị ảnh hưởng bởi trường hấp dẫn như theo Einstein. Tôi biết rằng cách truyền thống người ta giảng dạy vật lí lỗ đen là trong một mô tả thống nhất của sự cong của không gian và thời gian. Thật vậy, sẽ rất khó cho tôi mô tả cái gì xảy ra nếu như chúng ta rơi vào trong lỗ đen mà không nói tới sự cảm nhận thời gian của chúng ta đã thay đổi như thế nào. Tuy nhiên, toàn bộ khái niệm thời gian đã bị công trình của Einstein là cách mạng hóa tới mức nó xứng đáng được giới thiệu kĩ lưỡng hơn và trang trọng hơn với những người không chuyên vật lí. Do đó, trong chừng mực có thể, tôi sẽ hoãn phần trình bày về bản chất của thời gian, cái bên trong và bên ngoài lỗ đen, cho đến phần cuối tập sách này.