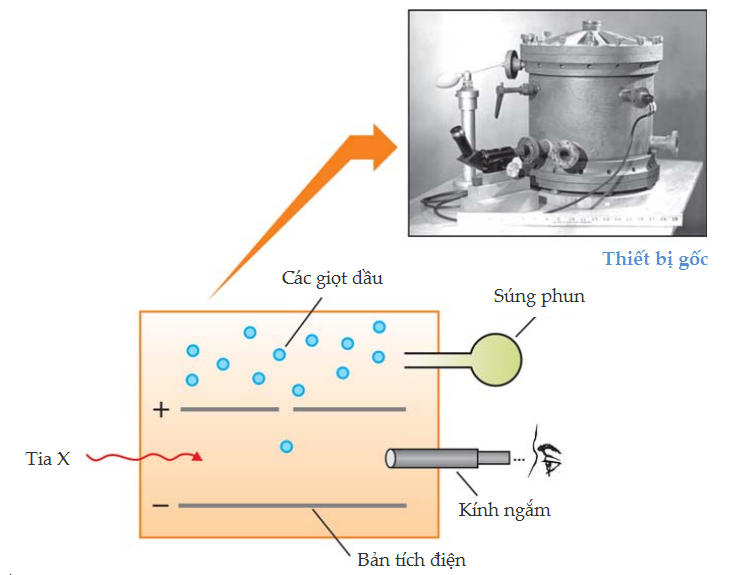
Không gian cao su
Trong Chương 1, tôi đã trình bày rằng không nên nghĩ không gian là “nơi đặt cái gì đó vào”, mà thay vậy nó có những tính chất hình học của riêng nó. Những tính chất này thay đổi trong sự có mặt của khối lượng. Để hình dung không gian có thể cong như thế nào ở gần một vật khối lượng lớn, chúng ta sẽ sử dụng thủ thuật bỏ đi một trong các chiều không gian và hãy nghĩ tới sự cong của một thế giới 2D.
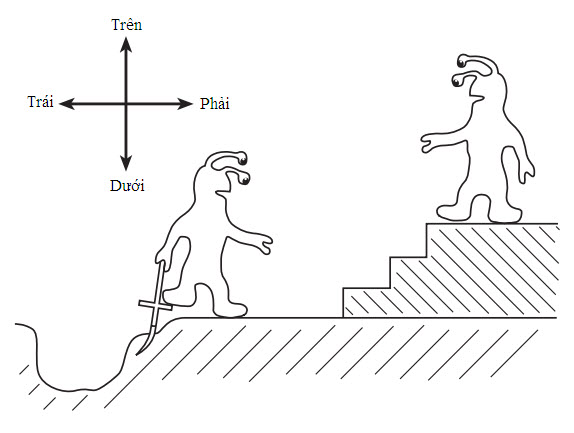
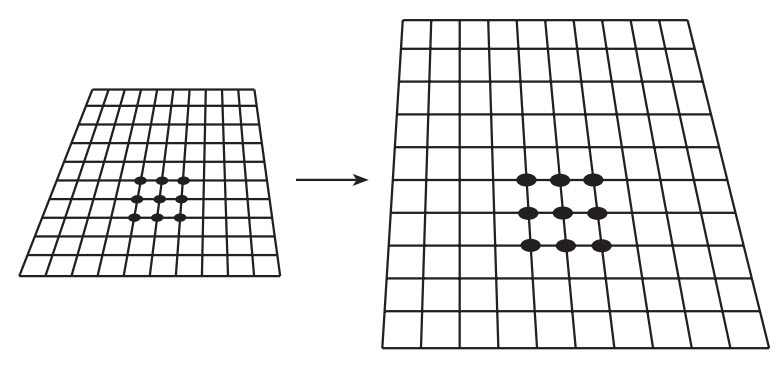
Cách tốt nhất để hiểu cái xảy ra với không gian khi ta đưa một vật khối lượng lớn vào là hãy tưởng tượng không gian (2D) đó giống như một tấm cao su. Hãy tưởng tượng lăn một quả cầu nhỏ trên một tấm bạt. Nó sẽ đi qua theo một đường thẳng. Giờ thì sẽ như thế nào nếu bạn đứng ở ngay giữa tấm bạt và nhờ ai đó lăn quả cầu đó một lần nữa? Bạn sẽ tạo ra một chỗ lõm làm cho chất liệu của tấm bạt hơi vồng xuống một chút. Nếu đường đi của quả cầu đủ gần so với chỗ lõm này, nó sẽ đi theo sự cong đó và uốn vòng để chuyển động theo một hướng khác (hình 2.2). Nhìn từ trên xuống, như thể bạn đã tác dụng một lực bí ẩn lên quả cầu làm cho nó bị hút về phía bạn và đi ra khỏi quỹ đạo thẳng ban đầu của nó. Đây là cách chúng ta hình dung vật chất uốn cong không gian xung quanh nó. Sự cong làm cho những vật khác đi theo một đường đi khác với đường chúng sẽ đi nếu không có sự cong đó. Cái xảy ra trên tấm bạt là quả cầu đang đi theo một đường trắc đạc. Đây là đường đi ưu tiên đối với quả cầu; đường đi mà nó nhận tự nhiên nhất, biết trước sự cong của chất liệu tấm bạt mà nó gặp. Như vậy, một đường trắc đạc là khoảng cách ngắn nhất giữa hai điểm bất kì. Cho nên, nếu có ai hỏi bạn khoảng cách ngắn nhất giữa hai điểm là bao nhiêu, thì đừng bao giờ nói đó là một đường thẳng. Đường trắc đạc chỉ là đường thẳng khi không gian là phẳng. Nếu quả cầu chuyển động chậm hơn cũng trên đường đi đó trên tấm thảm, thì nó sẽ gặp chỗ trũng và chuyển động xoắn ốc về phía chân của bạn.
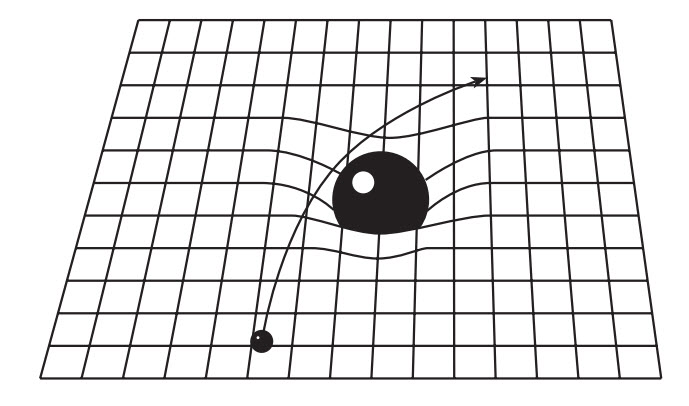
Hình 2.2 Vì một vật khối lượng lớn như một ngôi sao hay hành tinh tạo ra một vết lõm trong không gian, nên quỹ đạo của những vật nhỏ hơn đi qua gần sẽ bị uốn cong bởi chỗ “trũng” đó. Sự cong này là cái chúng ta gán cho lực hút hấp dẫn.
Trong ví dụ trên, chất liệu của tấm thảm thể hiện không gian 2D và vì thế sự tương tự là không chặt chẽ vì toàn bộ các vật trong không gian tưởng tượng này phải cư trú trong hai chiều, trong khi quả cầu là một vật thể 3D lăn phía trên bề mặt đó. Tương tự, vết lõm mà bạn tạo ra bằng cách đứng trên tấm thảm thật ra là do lực hấp dẫn của Trái đất hút bạn xuống, trong khi tôi đang yêu cầu bạn tưởng tượng rằng chỉ riêng khối lượng của bạn đang uốn cong bề mặt 2D đó. Trên thực tế, vì bạn là một vật thể 3D trong không gian 3D, nên thật ra cái bạn đang làm là uốn cong không gian thật sự xung quanh bạn. Tuy nhiên, hiệu ứng này quá nhỏ nên nó chưa bao giờ được đo thấy. Tuy vậy, đúng là hễ khi nào bạn ăn kiêng, không những bạn hi vọng có được vùng eo phẳng hơn – cái tôi cảm thấy khó khăn trong những năm gần đây – mà không gian xung quanh bạn cũng sẽ hơi phẳng hơn một chút vì bạn có khối lượng kém đi!
Giờ thì ta có thể hiểu cách lí giải của Einstein về lực hấp dẫn. Tất cả các đối tượng vật chất uốn cong không gian xung quanh chúng đi một lượng phụ thuộc vào khối lượng mà chúng có, và không gian bị uốn cong này khi đó dẫn hướng tất cả các vật chuyển động bên trong nó, làm cho chúng đi theo những đường trắc đạc. Những quỹ đạo như thế có thể hiểu được nếu bạn nghĩ tới đường bay của một chiếc máy bay.
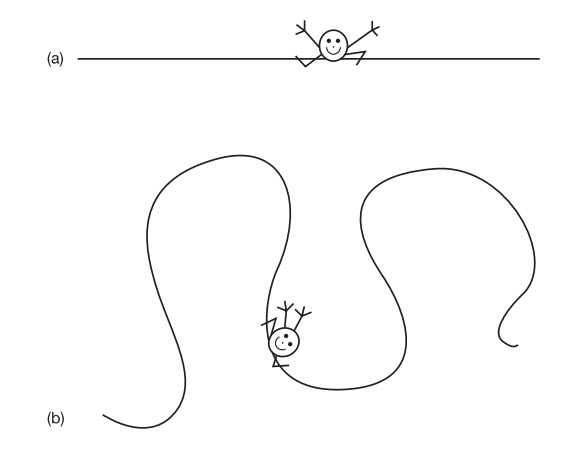
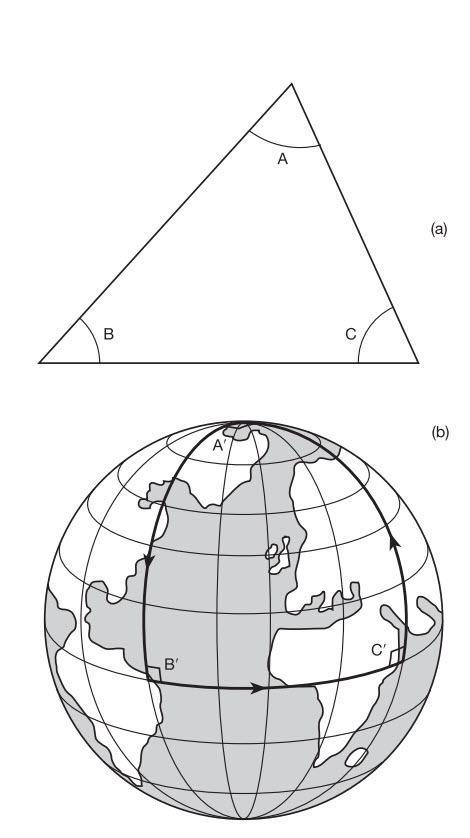
Mấy năm trước, tôi có bay từ London sang Tokyo dự một hội nghị vật lí. Tôi nhìn vào tấm bản đồ thế giới của mình để có một chút ý niệm mơ hồ về những đất nước mà tôi sẽ bay ngang qua. Tôi quên rằng một tấm bản đồ là hình chiếu phẳng của bề mặt cong của Trái đất. Cho nên, mặc dù khoảng cách ngắn nhất giữa hai điểm trên tấm bản đồ (ví dụ giữa London và Tokyo) có thể trông là một đường thẳng trên trang giấy, nhưng để tìm khoảng cách ngắn nhất, chúng ta nên nhìn vào quả địa cầu. Để tìm khoảng cách này, ta đặt một đầu dây cao su lên London, còn đầu kia đặt lên Tokyo. Sợi dây sẽ luôn uốn theo một đường trắc đạc vì đây sẽ là khoảng cách ngắn nhất giữa hai điểm. Mọi đường đi khác sẽ là dài hơn và khiến sợi dây dãn ra nhiều hơn. Vì nó có một xu hướng tự nhiên là giảm thiểu chiều dài của nó, nên nó luôn tìm lộ trình đòi hỏi dãn ra ít nhất. Giờ chúng ta thấy lộ trình bay – giả sử người phi công muốn giảm thiểu nhiên liệu tiêu thụ và không trệch khỏi đường trắc đạc do thời tiết xấu hoặc do vùng cấm bay của một nước nào đó – sẽ đi qua một vùng xa về phía bắc của cả London và Tokyo, một lộ trình trông có dạng cong nếu bạn vẽ trên một bản đồ phẳng.
Bây giờ, khi tôi giới thiệu quan niệm của Einstein về lực hấp dẫn, chúng ta có thể nhìn vào một số hệ quả thú vị hơn của nó, thí dụ một cái lỗ trong không gian mà mọi thứ có thể rơi vào trong đó và bị mất vĩnh viễn: một lỗ đen. Bạn sẽ khám phá ra rằng những vật thể kì lạ như thế là hiện thực khoa học chứ không phải viễn tưởng vì các nhà thiên văn học ngày nay gần như chắc chắn rằng các lỗ đen thật sự tồn tại trong vũ trụ.
Để lát đường cho việc thảo luận về lỗ đen, trước tiên ta cần tìm hiểu đôi chút về cách thức chúng có thể hình thành. Để có lỗ đen, không gian cần bị uốn cong một lượng vô hạn. Điều này đòi hỏi cái gì đó thật sự rất đậm đặc. Cho dù toàn bộ Trái đất vẫn là không đủ - tiện thể, nó cũng bác bỏ khả năng Tam giác Bermuda là một loại hang lỗ trong không gian nuốt chửng lấy những con tàu và máy bay kém may mắn, vì một cái lỗ có kích cỡ như thế sẽ đòi hỏi một khối lượng lớn hơn nhiều so với toàn bộ hành tinh, và chúng ta có thể dễ dàng tính ra khối lượng của Trái đất từ cách nó quay xung quanh Mặt trời.
Cái chúng ta cần cho sự uốn cong khủng khiếp của không gian là cái gì đó to lớn, thí dụ như một ngôi sao.
Lỗ đen, lỗ sâu đục và cỗ máy thời gian
Jim Al-Khalili
Bản dịch của Thuvienvatly.com







![[Ảnh] Vết tích đổ bộ của xe tự hành Curiosity](/bai-viet/images/2012/08/curiosityima.jpg)