1
CHIỀU THỨ TƯ
Nghiên cứu các hình dạng
Hình học là ngành toán học nghiên cứu tính chất và quan hệ của các điểm, các đường, các mặt, và các khối. Đa số mọi người có lẽ không thèm nhìn lại kiến thức hình học họ đã học ở trường phổ thông: diện tích của một hình tròn, chiều dài các cạnh của một tam giác vuông, thể tích của hình lập phương và hình trụ, không quên những công cụ xác thực đó, compa và thước đo góc, với sự say mê tiếc nuối. Vì thế, tôi không hi vọng bạn sẽ không quá phớt lờ một chương dành riêng cho hình học.
Theo tinh thần viễn chinh của cuốn sách này là chống lại ngôn ngữ chuyên ngành khoa học, tôi sẽ định nghĩa lại hình học bằng cách nói nó phải nghiên cứu các hình dạng. Ta hãy xét cái ta cho là hình dạng với ý nghĩa chung nhất. Hãy nhìn vào chữ “S”. Hình dạng của nó là do một đường cong tạo ra. Một vết nước sơn trên miếng vải bạt cũng có một hình dạng nào đó, nhưng đây không còn là hình dạng của một đường mà là của một mặt. Các vật rắn cũng có hình dạng. Khối lập phương, quả cầu, con người, xe hơi đều có hình dạng hình học gọi là hình khối.
Tính chất khác nhau trong ba trường hợp ở trên – đường, mặt và khối – là số chiều cần thiết để định nghĩa chúng. Người ta nói một đường thẳng là một chiều, hay 1D cho gọn, một mặt là hai chiều, hay 2D, và một khối là 3D.
Có lí do nào khiến tôi không nêu tiếp những chiều cao hơn không? Có gì đặc biệt với con số ba mà chúng ta phải dừng lại ở đó? Câu trả lời, tất nhiên, là chúng ta đang sống trong một vũ trụ có ba chiều không gian; chúng ta có sự tự do chuyển động tới/lui, sang trái/sang phải, và lên/xuống, nhưng ta không thể hướng theo một chiều mới vuông góc với ba chiều kia. Trong toán học, ba chiều trong đó chúng ta tự do chuyển động được gọi là vuông góc lẫn nhau, đó là cách các nhà toán học nói “vuông góc với nhau”.
Tất cả những vật rắn xung quanh chúng ta là 3D. Cuốn sách bạn đang đọc có một chiều cao, chiều rộng và bề dày nhất định (cả ba đại lượng là chiều dài đo theo những hướng vuông góc lẫn nhau). Ba con số này cùng xác định kích cỡ của cuốn sách. Thật vậy, nếu bạn nhân những con số trên với nhau, bạn sẽ có thể tích của nó. Điều này không rõ ràng cho lắm đối với mọi vật rắn. Một quả cầu, chẳng hạn, chỉ cần một con số để xác định kích cỡ của nó: bán kính của nó. Nhưng nó vẫn là ba chiều vì nó là một vật rắn nằm trong không gian 3D.
Chúng ta thấy những hình dạng xung quanh mình hoặc là một, hoặc hai, hoặc ba chiều, không bao giờ là bốn chiều vì những vật như thế không thể nào trú ngụ trong không gian ba chiều của chúng ta. Thật vậy, chúng ta thậm chí không thể tưởng tượng một hình dạng bốn chiều sẽ trông như thế nào. Tưởng tượng ra cái gì đó có nghĩa là xây dựng một mô hình trí tuệ của nó trong não của chúng ta vốn chỉ có thể hình dung ba chiều là tối đa. Chúng ta, hơi theo nghĩa đen một chút, sẽ không thể nào mường tượng ra trong đầu một hình dạng 4D.
Đối với nhiều người, “một chiều” có nghĩa là “theo một hướng”. Thêm một chiều nữa vào có nghĩa là cho phép nó chuyển động theo một hướng mới. Đủ đúng, nhưng bạn có thể hỏi, còn về kí tự “S” thì sao? Khi viết chữ “S”, ngòi bút của bạn lần theo những đường cong theo những hướng khác nhau. Làm thế nào hình dạng cuối cùng đó vẫn là 1D cơ chứ? Hãy tưởng tượng một cái chấm tên là Fred sống trên một đường thẳng (hình 1.1). Fred không thể di chuyển ra khỏi đường thẳng đó và bị cấm chuyển động lên hoặc xuống. Ta nói chuyển động của nó là một chiều. Thật vậy, vì đường thẳng đó là toàn bộ vũ trụ của nó, nên ta nói Fred sống trong một vũ trụ 1D. Nhưng nếu vũ trụ của nó là kí tự “S” thì sao? Giờ thì nó sống trong bao nhiêu chiều? Câu trả lời vẫn là một. Nó vẫn bị cấm chuyển động lên hoặc xuống cái đường đó. Vui nhỉ, cuộc sống của nó bây giờ đã thú vị hơn rồi, vì nó có vài chỗ cong rẽ để xử lí, nhưng sự bẻ cong một hình dạng không làm tăng số chiều của nó. (Tiện thể, vì bản thân Fred chỉ là một cái chấm, hay một “điểm” mang lại cho nó sự định nghĩa toán học, nên nó là một sinh vật không có chiều).
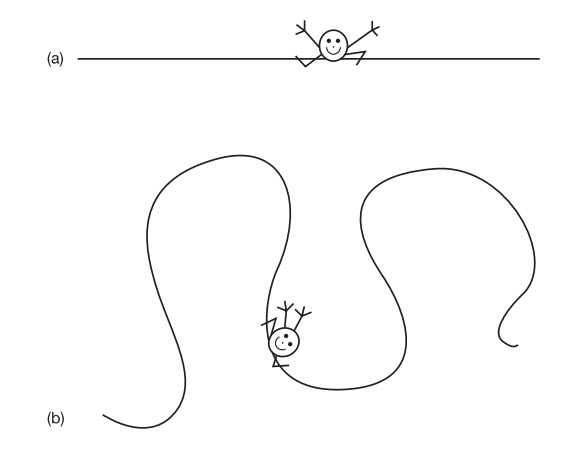
Hình 1.1 Cái chấm Fred sống trong vũ trụ một chiều của nó là (a) phẳng và (b) cong.
Một cách khác nói về các chiều của một không gian là nhìn xem có bao nhiêu con số, gọi là tọa độ, chúng ta cần để xác định một vị trí nhất định trong không gian đó. Ví dụ sau đây, tôi nhớ mình đã đọc hồi những năm trước nhưng không nhớ đã đọc ở đâu, là ví dụ rõ ràng nhất mà tôi biết. Hãy tưởng tượng bạn đang ở trên một chiếc sà lan đang đi qua một con kênh đào. Cho biết một điểm mốc nào đó, ví dụ ngôi làng bạn vừa đi qua, bạn chỉ cần một con số: quãng đường bạn đã đi tính từ ngôi làng đó, để xác định vị trí của bạn. Nếu sau đó, bạn quyết định dừng lại ăn trưa, bạn có thể gọi điện thoại cho một người bạn và thông báo cho họ biết bạn đang ở, nói thí dụ, cách ngôi làng trên sáu dặm theo hướng ngược dòng. Cho dù con kênh đào có ngoằn ngoèo ra sao, sáu dặm đó là quãng đường bạn đã đi, chứ không phải “đường chim bay”. Vì thế, ta nói chiếc sà lan bị hạn chế chuyển động trong một chiều, mặc dù nó không hoàn toàn phải đi theo đường thẳng.
Còn nếu bạn đang ở trên một con tàu trên đại dương thì sao? Giờ bạn cần hai con số (tọa độ) để xác định vị trí của bạn. Hai con số này sẽ là vĩ độ và kinh độ so với một điểm mốc nào đó, ví dụ như hải cảng gần nhất hay hệ tọa độ địa lí quốc tế. Vì thế, con tàu chuyển động trong hai chiều.
Mặt khác, đối với một con tàu ngầm, bạn cần ba con số. Ngoài vĩ độ và kinh độ, bạn còn phải chỉ rõ chiều dài trong một chiều thứ ba, độ sâu của nó. Và vì thế ta nói con tàu ngầm tự do chuyển động trong không gian ba chiều.
Lỗ đen, lỗ sâu đục và cỗ máy thời gian
Jim Al-Khalili