Không gian cong
Tôi đã đề cập rằng thế giới 2D tưởng tượng này không nhất thiết vô hạn về quy mô và do đó sẽ có một cái rìa, một đường biên nào đó xác định ranh giới của nó. Chúng ta sẽ thấy sau này rằng các vũ trụ không có biên và vì vậy thế giới 2D có lẽ phải trải ra vô hạn. Hóa ra điều này chỉ xảy ra (nghĩa là trải ra vô hạn) nếu thế giới 2D là phẳng, đó là cái cho đến đây tôi đã giả sử. Vậy còn những cư dân của thế giới 2D sống trên bề mặt của một quả cầu thì sao? Không gian của chúng bây giờ là không gian cong và không còn vô hạn về kích cỡ nữa. Rốt cuộc, một quả cầu thì có một diện tích bề mặt hữu hạn nhất định rõ ràng không có biên giới vì cư dân 2D có thể di chuyển khắp nơi trong vũ trụ này mà không bao giờ đi tới một điểm nào mà vượt ngoài đó chúng không thể đi. Khái niệm quan trọng và có phần thủ thuật để hiểu đúng ở đây là mặc dù thế giới 2D là bề mặt của một quả cầu 3D, nhưng phần bên trong quả cầu đó và tất cả không gian bên ngoài bề mặt đó không cần thiết tồn tại miễn là cư dân 2D không bận tâm. Vì vậy, theo một ý nghĩa nào đó, sự tương tự với con người sinh sống trên bề mặt Trái đất không nên nhấn mạnh quá vì chúng ta rõ ràng là những sinh vật 3D sống bám trên bề mặt của một quả cầu 3D. Cư dân 2D chỉ truy xuất bề mặt 2D. Phần bên trong của quả cầu thậm chí không tồn tại đối với chúng.
Câu hỏi hấp dẫn mà tôi muốn nêu ra tiếp sau đây là những cư dân 2D đó có biết không gian của chúng bị cong hay không?
Một cách cho chúng tìm ra câu trả lời là cách chúng ta có thể chứng minh Trái đất là không phẳng: để một người nào đó đi theo một hướng và cuối cùng trở về điểm xuất phát từ phía ngược lại đã đi qua vòng quanh địa cầu. Tất nhiên, ngày nay chúng ta thường xuyên đưa các nhà du hành vũ trụ lên quỹ đạo, họ có thể nhìn ngược về và thấy Trái đất tròn, nhưng những cư dân của thế giới 2D bị giam giữ trong bề mặt của chúng và không thể đi ra khỏi thế giới của chúng để nhìn trở xuống. Có một cách khác cho chúng kiểm tra xem thế giới của chúng có bị cong hay không.
Chúng ta đã biết ở trường phổ thông rằng nếu ta cộng giá trị ba góc trong của một tam giác bất kì, ta luôn có được 180 độ. Cho dù chúng ta vẽ tam giác lớn hoặc nhỏ bao nhiêu, hay hình dạng của nó ra sao; câu trả lời sẽ luôn luôn giống nhau. Nếu nó là một tam giác vuông thì hai góc kia cộng lại phải bằng 90 độ. Nếu một trong các góc là tù, với giá trị, ví dụ, 160 độ, thì hai góc kia cộng lại phải bằng 20 độ còn lại, và vân vân. Nhưng trước khi bạn lao vào tự mãn đã vượt qua chút kiến thức hình học này, cho phép tôi phát biểu hàm hồ một chút rằng bài toán các góc của một tam giác cộng lại bằng 180 độ chỉ đúng nếu tam giác đó được vẽ trên một bề mặt phẳng! Một tam giác vẽ trên một mặt cầu có các góc cộng lại luôn lớn hơn 180 độ. Đây là một ví dụ đơn giản chứng minh cái tôi muốn nói. Để hình dung ra điều này, bạn cần một quả bóng và một cái bút lông.
Hãy tưởng tượng một nhà thám hiểm bắt đầu cuộc hành trình tại Cực Bắc. Anh đi theo một đường thẳng về phương Nam (khi bạn đứng tại Cực Bắc, hướng duy nhất bạn có thể đi là hướng Nam) băng qua chóp đông của Canada rồi băng xuống tây Đại Tây Dương. Tất nhiên, anh thận trọng lái qua Tam giác Bermuda, vì anh tin mọi sự mê tín là vô nghĩa. Anh giữ hướng Nam thẳng tiến cho đến khi đến xích đạo ở đâu đó bắc Brazil. Một khi tới xích đạo, anh rẽ trái, và nhắm hướng Đông xuyên Đại Tây Dương, giờ thì đi theo đường thẳng dọc theo xích đạo. Anh đi tới bờ biển châu Phi và đổ bộ đi tiếp tới Kenya, lúc ấy anh đã hưởng đủ bầu khí hậu nóng, ẩm và quyết định rẽ trái và thẳng hướng Bắc mà đi trở lại. Anh đi qua Ethiopia, Saudi Arabia, Trung Đông, đổ hành trình qua Đông Âu, rồi trở về Cực Bắc.
Nếu bạn vẽ đường đi hành trình của anh ta, bạn sẽ thấy rằng anh ta đã đi trọn một tam giác (hình 1.16(b)). Hãy nhìn kĩ vào ba góc. Lúc đi tới xích đạo và rẽ trái, anh đã tạo ra một góc vuông (90 độ). Nhưng khi cuối cùng anh rời xích đạo để quay về hướng bắc, anh đã tạo ra một góc vuông khác. Hai góc này cộng lại, do đó, bằng 180 độ. Nhưng chúng ta chưa tính đến góc anh ta tạo ra tại Cực Bắc với hai đường thẳng của hành trình đi ra và đi vào. Hai đường này đại khái cũng tạo ra một góc 90 độ, mặc dù tất nhiên kích cỡ của góc này phụ thuộc vào anh ta đã đi quãng đường bao xa trên đường xích đạo. Tôi đã chọn quãng đường đó sao cho anh ta vạch nên một tam giác, nối ba đường thẳng lại, với ba góc vuông cộng lại bằng 270 độ.
Một tam giác như vậy là một trường hợp đặc biệt vì quy tắc cơ bản là bất kì tam giác nào vẽ trên bề mặt của một quả cầu sẽ có các góc cộng lại lớn hơn 180 độ. Chẳng hạn, một tam giác nối Paris, Rome và Moscow có các góc cộng lại lớn hơn 180 độ một chút. Sự chênh lệch nhỏ như thế này so với 180 độ là vì một tam giác như vậy không bao quát một phần đáng kể của tổng diện tích bề mặt của Trái đất và do đó hầu như là phẳng.
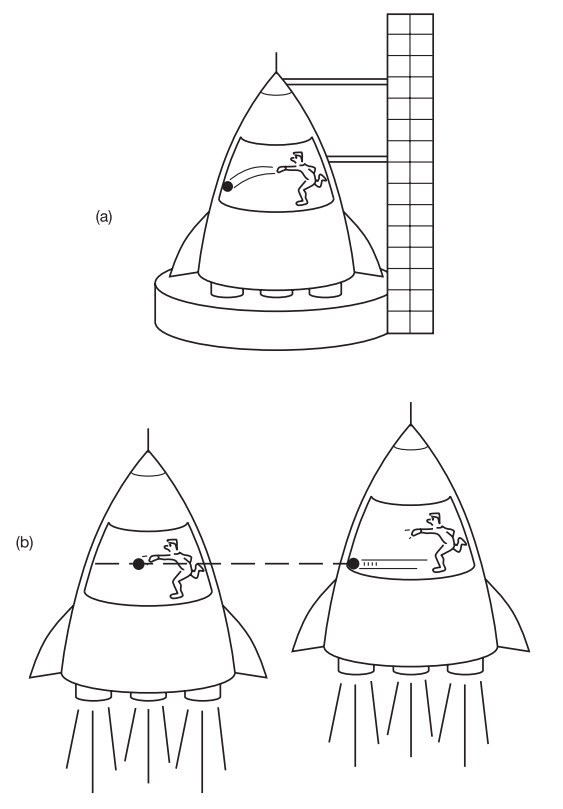
Trở lại với những cư dân 2D, chúng có thể sử dụng kĩ thuật tương tự để kiểm tra không gian của chúng có bị cong hay không. Chúng sẽ thẳng tiến trong một tên lửa 2D từ hành tinh quê hương của chúng đi theo đường thẳng cho đến khi chúng đi tới một ngôi sao ở xa. Tại đó, chúng sẽ rẽ hướng với một góc cố định cố định nào đó và thẳng tiến sang một ngôi sao khác. Một khi đến ngôi sao thứ hai, chúng sẽ quay đầu trở về. Đã vạch ra một tam giác, chúng sẽ đo ba góc. Nếu ba góc này cộng lại lớn hơn 180 độ3, thì chúng có thể suy luận rằng chúng sống trong không gian cong.
3Một bề mặt có thể cong theo một kiểu khác sao cho một tam giác vẽ trên đó sẽ có các góc cộng lại nhỏ hơn 180 độ, nhưng tôi sẽ nói tới trường hợp đó ở phần sau.
Một tính chất khác, bạn có thể nhớ từ trường học, là chu vi của một vòng tròn bằng pi nhân với đường kính của nó. Giá trị của pi, như chúng ta được học, có phần thập phân vô hạn không tuần hoàn. Có một nút bấm trên đa số máy tính bỏ túi cho giá trị pi lên tới 10 chữ số thập phân (3,1415926536), nhưng đa số chúng ta nhớ nó là 3,14. Vâng, tôi thừa nhận rằng tôi nhớ nó đến 10 chữ số thập phân mà máy tính bỏ túi trình bày, nhưng đó chỉ là vì tôi sử dụng nó trong công việc của mình quá thường xuyên, nó không khác gì với việc ghi nhớ một số điện thoại đặc biệt. Tuy nhiên, tôi có một người bạn nghiên cứu toán học biết pi đến 30 chữ số thập phân. Ngoài ra, anh ta khá bình thường. Chúng ta được học rằng pi là cái gọi là một hằng số toán học. Nó được định nghĩa là tỉ số của hai con số: chu vi và đường kính của một vòng tròn bất kì trong không gian phẳng. Nếu nhà thám hiểm của chúng ta đi vòng quanh Vòng cực Bắc, nó có đường kính mà anh có thể đo chính xác (nó bằng hai lần khoảng cách từ Vòng cực Bắc đến Cực Bắc), thì anh sẽ thấy việc nhân giá trị đường kính này với pi (đó là cách tính chu vi của vòng tròn), anh sẽ có giá trị hơi lớn hơn chu vi thật sự của Vòng cực Bắc. Sự cong của Trái đất có nghĩa là Vòng cực Bắc hơi nhỏ hơn so với nó nếu như Trái đất là phẳng.
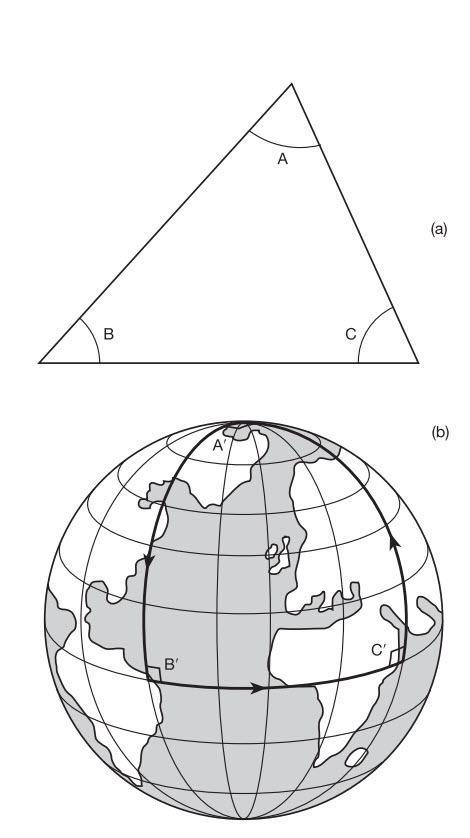
Hình 1.6 (a) Một tam giác vẽ trên một miếng giấy phẳng có ba góc trong A + B + C = 180o. (b) Một tam giác vẽ trên bề mặt của một quả cầu có các góc cộng lại lớn hơn 180o. Tam giác vẽ ở đây có ba góc 90o.
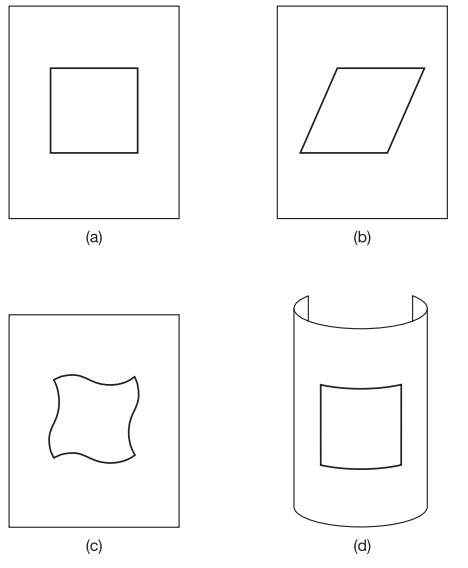
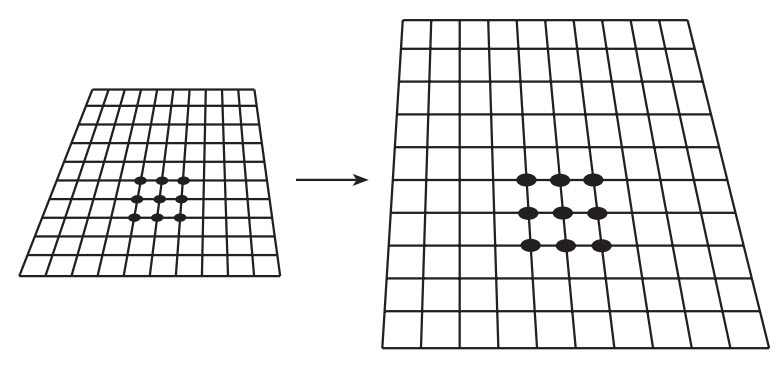
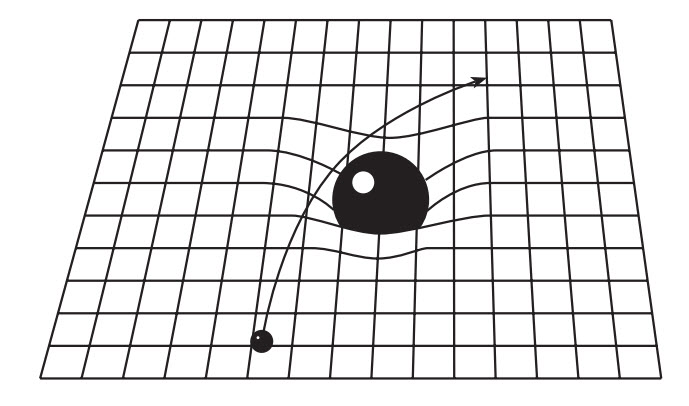
Tính chất của những tam giác và hình tròn mà chúng ta học được ở trường phổ thông là cái được gọi là hình học Euclid, hay “hình học phẳng”. Hình dạng 3D của những quả cầu, khối lập phương và kim tự tháp cũng là một phần của hình học Euclid nếu chúng được nhúng trong một không gian 3D phẳng. Tính chất của chúng thay đổi nếu như không gian 3D bị cong, theo kiểu giống với cách tính chất của những tam giác và vòng tròn thay đổi khi chúng được vẽ trên một không gian 2D cong như bề mặt của một quả cầu. Vì vậy, không gian 3D của chúng ta có lẽ bị cong nhưng chúng ta không cần hình dung ra một chiều thứ tư để “nhìn thấy” sự cong này. Ta có thể đo nó gián tiếp bằng cách nghiên cứu hình học của không gian 3D và những vật rắn bên trong nó. Trên thực tế, chúng ta chưa bao giờ từng nhìn thấy một sự sai lệch nào khỏi hình học Euclid vì chúng ta đang sống trong một bộ phận của Vũ trụ trong đó không gian gần như là phẳng nên chúng ta không bao giờ có thể phát hiện ra bất kì sự cong nào. Điều này tương tự như việc cố gắng phát hiện ra sự cong của Trái đất bằng cách vẽ một tam giác trên một sân bóng đá. Tất nhiên, một sân bóng đá thì không hoàn toàn phẳng lì. Tương tự, không gian có chứa những vùng cong ở đâu đó mà chúng ta sẽ thấy trong chương tiếp theo.
Còn nếu một chiều không gian thứ tư thật sự có tồn tại ngoài ba chiều của chúng ta thì sao? Ta có thể nói gì về những tính chất của nó? Cách tốt nhất là bắt đầu với việc hiểu rằng chiều thứ tư đối với chúng ta là chiều thứ ba đối với cư dân 2D. Hãy tưởng tượng bạn đang đứng tại tâm của một vòng tròn lớn vẽ trên một nền đất phẳng như vòng tròn ở giữa sân bóng đá. Nếu bây giờ bạn đi theo một đường thẳng theo bất kì hướng nào, bạn sẽ tiến về phía đường bao của vòng tròn. Hướng này được gọi là hướng xuyên tâm, vì khi bạn đi tới đường bao, bạn phải đi theo bán kính của vòng tròn. Mặt khác, một con chim đang đậu tại tâm vòng tròn có thể chuyển động theo một chiều thứ ba: hướng lên trên. Nếu nó bay thẳng đứng thì sẽ nó chuyển động ra xa tất cả các phần của vòng tròn trong suốt thời gian.
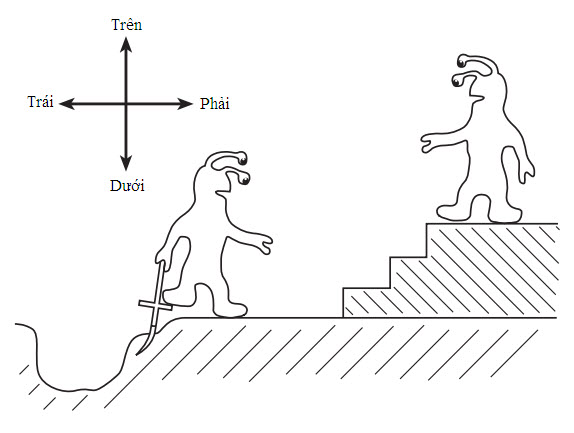
Giờ hãy bổ sung thêm một chiều nữa cho ví dụ này và hãy tưởng tượng con chim đậu tại tâm của một quả cầu (ví dụ một lồng chim hình cầu). Cho dù lúc này con chim bay theo hướng nào, nó sẽ chuyển động ra xa các thanh chắn lồng, và tất cả các hướng đối với nó giờ là xuyên tâm. Giống hệt như trong ví dụ vòng tròn 2D trong đó con chim có thể chuyển động theo chiều thứ ba ra khỏi vòng tròn, bây giờ ta có thể thấy chuyển động theo một chiều thứ tư sẽ có nghĩa là gì. Bắt đầu tại tâm lồng chim, đó là hướng trong đó con chim sẽ phải bay để chuyển động ra xa mọi điểm trên lồng trong suốt thời gian! Đây không phải là một hướng ta có thể từng hình dung ra vì, như tôi đã đề cập ở phần trước, não của chúng ta chỉ là ba chiều. Vậy thì chúng ta sẽ nhìn thấy gì nếu ta có một con chim thần, có khả năng khai thác chiều không gian thứ tư, bị nhốt trong một cái lồng? Chúng ta sẽ thấy nó biến mất khỏi tầm nhìn và sau đó xuất hiện trở lại không gian 3D của chúng ta ở chỗ nào đó khác, có khả năng ở bên ngoài cái lồng. Điều đó trông lạ lùng đối với chúng ta giống hệt như những kĩ năng 3D của chúng ta làm kinh ngạc những cư dân 2D khi chúng ta lấy các vật ra khỏi không gian 2D của chúng.
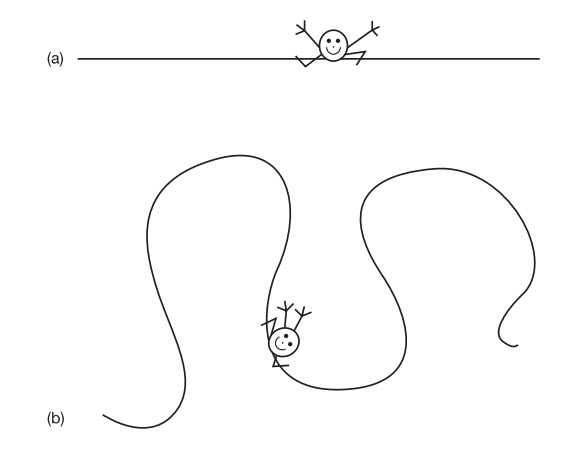
Một hiệu ứng thú vị khác của việc sử dụng một chiều cao hơn là cái xảy ra khi các vật bị lật ngược. Hãy tưởng tượng bạn có thể nâng một cư dân 2D ra khỏi thế giới của nó, quay nó sao cho bên trái thành bên phải, rồi đặt nó trở xuống. Mọi thứ đối với nó trong khoảnh khắc sẽ có phần lạ lùng. Nó sẽ không cảm thấy sự khác biệt nào nhưng mọi thứ xung quanh nó dường như đang ở lộn bên. Nó sẽ phải thích nghi để sống trong một thế giới trong đó mặt trời 2D không còn mọc lên từ bên phải như nó quen thuộc mà từ phía bên trái. Và lúc này từ nhà nó phải đi theo hướng ngược lại để đến chỗ làm.
Mọi thứ sẽ còn lạ lùng hơn nếu bạn xét thế giới sẽ trông như thế nào đối với bạn khi một sinh vật 4D nhặt bạn ra khỏi thế giới 3D và lật ngược bạn lại. Lúc đầu, mọi người sẽ để ý thấy cái gì đó hơi khác với diện mạo của bạn vì gương mặt của bạn lúc này trước mắt họ giống như gương mặt của bạn ở trong gương. Sau đó, nếu bạn nhìn vào gương soi, bạn cũng sẽ thấy sự khác biệt. Đây là vì không có gương mặt của ai là đối xứng cả. Phía bên trái gương mặt của bạn khác với phía bên phải. Có lẽ một con mắt nằm hơi cao hơn con mắt kia hoặc, giống như tôi, mũi của bạn hơi nghiêng về một bên, hoặc bạn có một nốt ruồi trên má, và vân vân. Nhưng đây mới là cái bắt đầu trong số những trở ngại của bạn. Mọi thứ xung quanh bạn xuất hiện từ sau ra trước. Toàn bộ chữ viết đều bị ngược, kim đồng hồ thì quay ngược chiều, và giờ bạn sẽ thuận tay trái nếu trước đó bạn thuận tay phải. Một cách kiểm tra thế giới như vậy trông như thế nào đối với bạn là hãy đi vòng vòng và nhìn thế giới trong gương. Cẩn thận kẻo bị va vào các thứ xung quanh bạn nhé.
Lỗ đen, lỗ sâu đục và cỗ máy thời gian
Jim Al-Khalili






![[Ảnh] Bão cát](/bai-viet/images/2013/01b/baocat01.jpg)





