Lỗ đen, lỗ sâu đục và cỗ máy thời gian (Phần 16)

Vũ trụ giãn nở

Ngày nay, nhiều người không phải nhà khoa học cũng biết tới khái niệm Vũ trụ giãn nở. Nhưng nó có nghĩa là gì? Có phải nó là một quan niệm lạ nữa mà các nhà khoa học nghĩ ra dựa trên dăm ba bằng chứng rằng nó có thể được lí giải theo một cách khác? Câu trả lời là không phải vậy. Ngày nay, có quá nhiều bằng chứng ủng hộ quan sát cho rằng Vũ trụ của chúng ta đang ngày một to ra nên chúng ta không còn phải nghi ngờ gì nữa. Sự giãn nở đã được xác nhận từ hồi năm 1929 khi nhà thiên văn học người Mĩ Edwin Hubble thực hiện một khám phá đáng chú ý, nhưng chỉ sau khi một số nhà vũ trụ học đã dự đoán hiệu ứng trên lí thuyết.

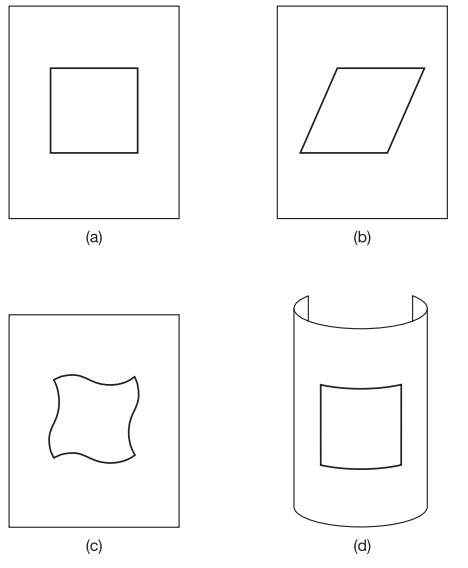
Tất nhiên, nhà vũ trụ học hiện đại đầu tiên chính là Einstein. Không bao lâu sau khi hoàn thành thuyết tương đối tổng quát của ông vào năm 1915, ông bắt đầu sử dụng các phương trình của mình để mô tả những tính chất tổng thể của toàn Vũ trụ. Ông sớm vướng mắc một vấn đề nghiêm trọng. Nếu, tại một thời điểm cho trước, toàn bộ các thiên hà trong Vũ trụ là đứng yên so với nhau, và biết rằng Vũ trụ là hữu hạn về kích cỡ, thì lực hút hấp dẫn tương hỗ của chúng sẽ làm cho chúng bắt đầu tụ lại với nhau và Vũ trụ sẽ tự co lại. Nó không thể nào tĩnh tại nữa. Thật ra đây chỉ là một thí dụ có tính thu hút (và không phải là thí dụ duy nhất chúng ta sẽ gặp trong chương này). Đấy là vì, một cách chất phác, bạn nghĩ Vũ trụ được xác định bởi thể tích không gian của nó vẫn giữ nguyên kích cỡ như cũ trong khi vật chất mà nó chứa bị hút hấp dẫn về phía “tâm” của nó. Điều này khá sai lầm. Trước tiên, chúng ta sẽ thấy rằng Vũ trụ không có tâm gì cả và, trong mọi trường hợp, chúng ta đã học được rằng lực hấp dẫn ảnh hưởng đến bản thân không gian chứ không đơn giản tác dụng lên vật chất “bên trong” nó.

Tiên đoán của những phương trình của ông đã khiến Einstein lo lắng. Quan điểm được chấp nhận rộng rãi vào lúc đó, và Einstein không là ngoại lệ bất chấp nhiều quan niệm mang tính cách mạng khác của ông, là rằng Vũ trụ, ở quy mô thiên hà và lớn hơn, sẽ là tĩnh tại và bất biến. Do đó, cho dù nó đã hiện hữu vĩnh hằng hay có một đấng sáng thế thiêng liêng đã đưa nó vào tồn tại ngay một thời điểm nào đó trong quá khứ xa xôi là không thành vấn đề. Cả hai quan điểm đều ủng hộ một bức tranh Vũ trụ hiện nay là không đổi. Quan niệm về một vũ trụ phát triển là mang tính con người và không cần thiết. Vì thế, khi các phương trình của thuyết tương đối tổng quát của Einstein dường như báo hiệu Vũ trụ đang co lại, ông đã quyết định phải hàn gắn mọi thứ lại. Ông cho rằng, để làm cân bằng lực hấp dẫn hướng vào trong, cần có một lực phản hấp dẫn ngược lại, gọi là lực đẩy vũ trụ, lực sẽ làm cân bằng lực hút hấp dẫn và giữ cho các thiên hà ở xa nhau và Vũ trụ ổn định. Sự khác biệt giữa lực hấp dẫn và lực phản hấp dẫn là tựa như sự khác biệt giữa lực hút kéo cực bắc của nam châm này về phía cực nam của nam châm kia và lực đẩy tách hai cực bắc ra xa nhau. Lực đẩy vũ trụ này xuất hiện trong toán học dưới dạng một con số, cái Einstein gọi là hằng số vũ trụ học. Nó được kí hiệu trong các phương trình của ông bằng kí tự Hi Lạp lambda. (Trong toán học cao cấp, việc dùng x, y, z cho những đại lượng chưa biết là không đủ. Chúng ta sớm dùng hết các kí tự trong bảng chữ cái và bắt đầu vay mượn các kí tự Hi Lạp – với pi là ví dụ được biết tới nhiều nhất trong số này) Cái Einstein đã đề xuất là một thủ thuật toán học để thu được mô hình vũ trụ tĩnh của ông.

Một vài năm sau công trình khởi nguồn của Einstein, nhà vũ trụ học Soviet Aleksandr Friedmann cho công bố một bài báo trong đó ông đề xuất loại bỏ lực đẩy vũ trụ (bằng cách đặt giá trị của hằng số vũ trụ học bằng không trong các phương trình Einstein). Friedmann nhận thấy khi ông áp dụng các phương trình của thuyết tương đối tổng quát Einstein cho Vũ trụ và thực hiện các phép tính, ông luôn tìm ra những nghiệm (những phương trình khác) dự đoán rằng khoảng cách giữa hai điểm bất kì trong không gian đang giãn ra theo thời gian. Ông đã tìm thấy trên lí thuyết rằng Vũ trụ đang to dần ra theo thời gian. Hai nhà khoa học khác cũng đi đến kết luận tương tự gần như đồng thời. Họ là nhà thiên văn học người Hà Lan Willem de Sitter và nhà vũ trụ học (và linh mục) người Bỉ Georges Lemaitre.

Kết quả này có phần khá bất ngờ nếu chúng ta nghĩ tác dụng của lực hấp dẫn sẽ như thế nào khi không có lực đẩy vũ trụ để giữ vật chất trong Vũ trụ ngừng ra xa nhau. Chắc chắn, nếu không có lực đẩy vũ trụ thì Vũ trụ sẽ đang co lại chứ không nở ra. Nhưng một vũ trụ đang giãn nở có thể hiểu theo kiểu sau đây. Hãy tưởng tượng một cái gì đó đã đưa Vũ trụ vào giãn nở lúc ban đầu, một vụ nổ khởi phát. Lực hút hấp dẫn của toàn bộ vật chất trong Vũ trụ khi đó sẽ làm chậm tốc độ giãn nở đi. Đây là cốt lõi lập luận của Friedmann. Nếu không có lực đẩy vũ trụ để cân bằng với lực hút hấp dẫn, và Vũ trụ đã bắt đầu giãn nở thì tại một thời điểm, Vũ trụ hoặc là đang nở ra hoặc là đang co lại. Nó không thể ở tình trạng lưng chừng giữa sự giãn và sự co vì như thế sẽ là không cân bằng.

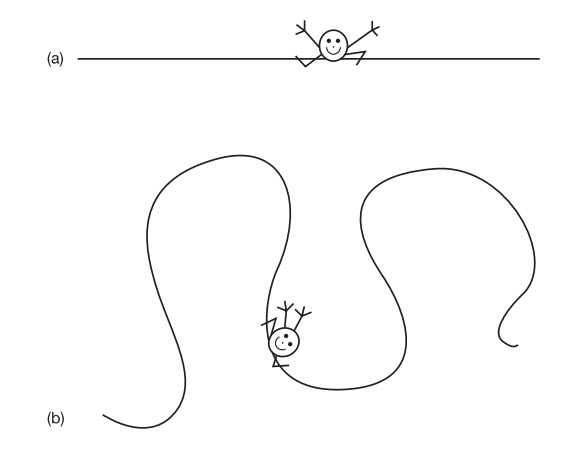
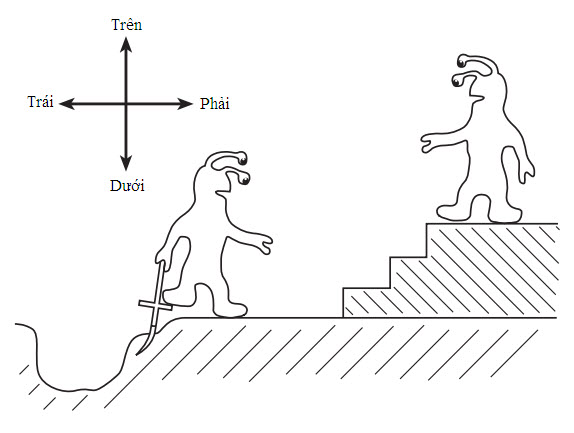
Một thí dụ đơn giản chứng minh cho lập luận này là cái xảy ra với một quả cầu nằm trên một mặt dốc nhẵn. Nếu ở lưng chừng dốc, nó sẽ luôn luôn lăn xuống. Nhưng nếu chúng ta không thấy lúc đầu làm thế nào quả cầu đã ở trên dốc thì ta sẽ muốn nó hoặc đang lăn lên dốc (tương ứng với một vũ trụ đang nở ra) hoặc đang lăn xuống dốc (một vũ trụ đang co lại), chứ không bao giờ đứng ở lưng chừng được. Tất nhiên, cách duy nhất để nó có thể lăn lên dốc thì nó đã được thận trọng cấp một cú đẩy ban đầu, nhưng trong trường hợp đó nó sẽ lập tức bắt đầu chậm dần và rồi cuối cùng bắt đầu lăn xuống trở lại. Giờ hãy tưởng tượng đến độ cao của đỉnh dốc. Ban đầu cho quả cầu lăn lên dốc đủ nhanh thì nó có thể lăn lên tới đỉnh dốc. Một khi ở đó, nó có thể tiếp tục lăn đi vô hạn định mà không chậm đi (tất nhiên ở đây tôi đang bỏ qua ma sát và sức cản của gió vì một quả cầu trên thực tế cuối cùng sẽ dừng lại trên một bề mặt phẳng).

Giả sử quả cầu luôn nhận được sự tốc độ ban đầu như nhau để lăn lên dốc, cái chi phối số phận tối hậu của nó khi đó sẽ là cái dốc cao bao nhiêu. Nếu nó quá cao thì quả cầu sẽ không bao giờ lăn lên tới đỉnh và sẽ lăn xuống trở lại.

Đây là cách chúng ta có thể xem xét sự giãn nở của Vũ trụ. Tác dụng của lực hút hấp dẫn phụ thuộc vào lượng vật chất mà Vũ trụ chứa. Ở đây tôi không chỉ muốn nói tất cả các ngôi sao, các hành tinh và những vật rắn khác, mà là mọi thứ chất trong Vũ trụ. Đây có thể là ở dạng bụi, chất khí, các hạt hạ nguyên tử, kể cả năng lượng thuần túy. Cho nên, Vũ trụ hiện nay đang co lại hay đang nở ra là phụ thuộc vào nó chứa bao nhiêu vật chất và lực hút hấp dẫn đã tác dụng lực hãm lên sự giãn nở ban đầu của nó mất bao lâu rồi. Đây là điều cốt lõi của vũ trụ mô hình của Friedmann.

Không ai, thậm chí cả Einstein, chuẩn bị sẵn tâm lí để tin vào các kết quả của Friedmann, mãi cho đến khi tìm thấy bằng chứng thực nghiệm. Bằng chứng này xuất hiện chỉ vài năm sau đó. Thật đáng tiếc, Friedmann đã qua đời vào năm 1925 nên không thể chứng kiến sự kiện này.