Không gian là gì?
Trong những cuộc họp nhân viên ở khoa vật lí tại trường Đại học Surrey nơi tôi làm việc, luôn luôn có một vấn đề trên bàn nghị sự gọi là “Không gian”. Đây là nơi những nhóm nghiên cứu khác nhau giành làm chỗ làm việc cho nghiên cứu sinh hoặc nhà nghiên cứu khách mời, họ cần một cái bàn làm việc trong một vài tuần hoặc chỗ trong phòng thí nghiệm cho những thí nghiệm của họ. Nhưng khi trưởng khoa đi tới vấn đề đó trong cuộc họp và phát biểu những câu đại loại như “Và bây giờ chúng ta chuyển sang vấn đề không gian” – thường thì luôn có ai đó lẩm bẩm – “trận tuyến cuối cùng đấy”. Bạn đừng nghĩ rằng nhà vật lí không có khiếu khôi hài nhé!
Chúng ta đều nghĩ chúng ta biết “không gian” nghĩa là gì, cho dù nó là không gian theo nghĩa “có một khoảng trống ở góc đó” hoặc “chẳng đủ chỗ cho con mèo nguẩy đuôi”, hay không gian theo nghĩa “không gian bên ngoài” theo kiểu trận tuyến cuối cùng vừa nói. Khi buộc phải suy nghĩ về nó, chúng ta sẽ nghĩ không gian đơn thuần là nơi để đặt cái gì đó vào. Bản thân không gian không phải là một chất. Điều này đa số chúng ta sẽ tán thành. Nhưng trong trường hợp đó, không gian có thể tồn tại hay không khi nó không chứa bất kì vật chất nào? Hãy nghĩ tới một cái hộp rỗng. Cho dù chúng ta bơm hết các phân tử không khí chứa trong nó sao cho thật sự chẳng còn có gì bên trong hộp, chúng ta vẫn sẽ hài lòng với khái niệm rằng không gian đó tiếp tục tồn tại. Không gian đó chỉ gợi đến thể tích của cái hộp.
Thật khó hình dung hơn khi không gian không có ranh giới. Chúng ta nghĩ không gian bên trong cái hộp chỉ tồn tại nhờ sự tồn tại của bản thân cái hộp. Vậy nếu ta gỡ bỏ nắp hộp và các thành hộp thì sao? Tất nhiên, nó vẫn tồn tại. Nhưng bây giờ nó là một vùng không gian là một phần của một vùng rộng lớn hơn bên trong căn phòng ta đang ở. Giờ ta hãy thử với một thứ rộng lớn hơn nữa: Vũ trụ của chúng ta về cơ bản là một thể tích chứa vật chất (các thiên hà, sao, tinh vân, hành tinh,…) rất lớn (có lẽ vô hạn). Vậy nếu Vũ trụ hoàn toàn trống rỗng và không chứa vật chất nào hết thì sao? Nó sẽ vẫn ở đó chứ? Câu trả lời là vâng, vì không gian không cần chứa vật chất để tồn tại. Ở đây, vấn đề trình bày dễ lao vào – vì tôi đang làm mọi việc trình bày, và tôi biết mình đang muốn làm gì – vấn đề mang tính kĩ thuật cao và nhập nhằng (nhưng gây nhiều tranh luận) gọi là nguyên lí Mach. Nguyên lí này phát biểu rằng không gian, hay ít nhất là những khoảng cách và chiều bên trong đó, là vô nghĩa khi nó không chứa vật chất nào. Ngoài ra, Einstein còn chỉ ra trong các lí thuyết tương đối của ông rằng không gian, giống như thời gian, cũng mang tính tương đối. Tuy nhiên, tôi không muốn đi quá sâu ở giai đoạn đầu này của tập sách và sẽ giả sử rằng mặc dù không gian không phải là một chất, tuy nhiên nó phải là cái gì đó!
Nhưng nếu không gian không phải là một chất, làm thế nào ta có thể tương tác với nó? Vật chất có thể ảnh hưởng đến nó theo kiểu nào đó hay không? Hóa ra vật chất thật sự có thể ảnh hưởng đến bản thân không gian: nó có thể bẻ cong không gian! Một khi bạn nhận thức đúng thực tế này, bạn sẽ không bao giờ bị ấn tượng nữa trước những khẳng định làm bẻ cong dao kéo bằng sức mạnh của trí tuệ (một trò ảo thuật rẻ tiền và khá vô vị).
Trong chương tiếp theo, tôi sẽ yêu cầu bạn tưởng tượng sự bẻ cong không gian 3D1. Thật dễ thôi, bạn có thể nghĩ vậy, tôi có thể dễ dàng bẻ cong một vật thể 3D như cuốn sách này. Vâng, không đơn giản như thế đâu. Bạn thấy đó, tôi không có ý nói những vật 3D đang bị bẻ cong bên trong không gian 3D, mà là sự bẻ cong bản thân không gian 3D.
1Để chính xác hơn, hễ khi nào tôi nói tới sự bẻ cong của không gian 3D, thật ra tôi sẽ nói sự bẻ cong của “không-thời gian” 4D. Đây là cái lí thuyết tương đối của Einstein nói chúng ta nên gọi cho sự kết hợp của ba chiều không gian với một chiều thời gian. Tuy nhiên, tôi sẽ gác phần trình bày không gian và thời gian hòa lẫn như thế nào trong phần cuối cuốn sách này.
Hãy nghĩ tới sự cong của đường 1D để tạo thành kí tự “S”. Chúng ta cần một tờ giấy 2D để viết chữ “S” trên đó. Ta nói hình dạng 1D đó được nhúng trong chiều cao hơn. Tương tự, sự bẻ cong một tờ giấy đòi hỏi sử dụng không gian 3D của chúng ta nếu ta muốn hình dung ra nó. Để nhận thức không gian 3D bẻ cong ra sao, ta phải tưởng tượng không gian 4D trong đó nó có thể bẻ cong.
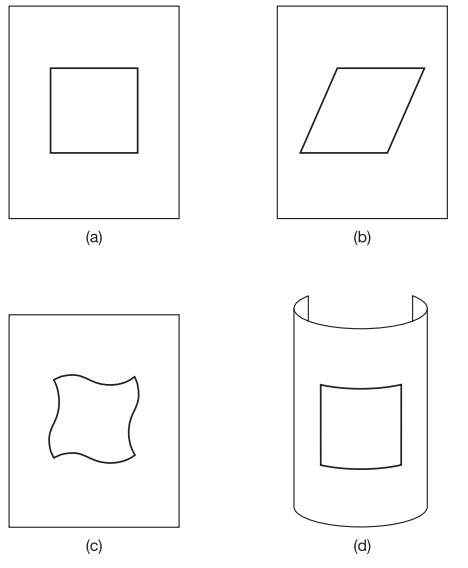
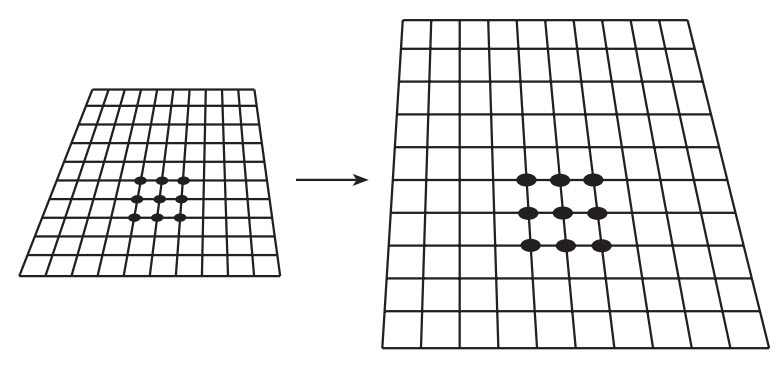
Hình 1.2 (a) Một hình vuông (hình 2D) vẽ trong một không gian 2D phẳng, (b và c) hình vuông đó có thể bẻ cong hoặc biến dạng bên trong không gian 2D phẳng hoặc (d) bản thân không gian 2D bị cong.
Nếu bạn vẫn còn chút băn khoăn về sự khác biệt giữa sự bẻ cong một vật rắn trong không gian và sự bẻ cong bản thân không gian, thì đây là một ví dụ đơn giản trong không gian 2D. Lấy một hình vuông vẽ một trên một mảnh giấy (hình 1.2(a)). Hình vuông đó có thể bẻ cong bên trong mặt 2D đó (mảnh giấy) để tạo ra một hình dạng khác. Thí dụ, hãy tưởng tượng đẩy hai góc đối diện sao cho nó tạo thành hình kim cương, như trong hình 1.2(b), hoặc có thể vẽ lại các đường cong quẹo như trong hình 1.2(c). Trường hợp này khá khác với bản thân mảnh giấy bị bẻ cong (hình 1.2(d)). Giờ thì hình vuông đó xuất hiện bị cong trước chúng ta mặc dù ta không vẽ lại nó; mà vì không gian trong đó hình vuông tồn tại đã bị cong.
Lỗ đen, lỗ sâu đục và cỗ máy thời gian
Jim Al-Khalili