Các thí nghiệm khác ngoài cân xoắn
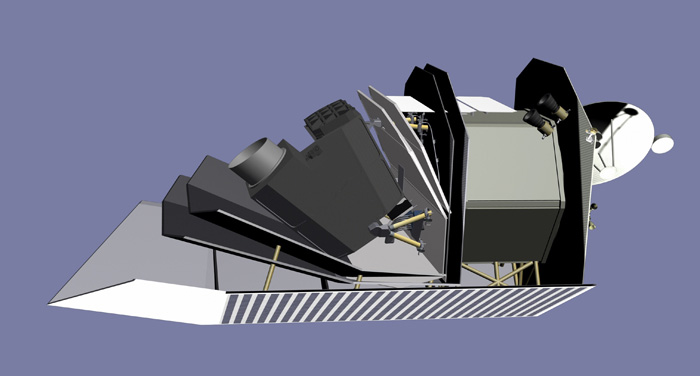
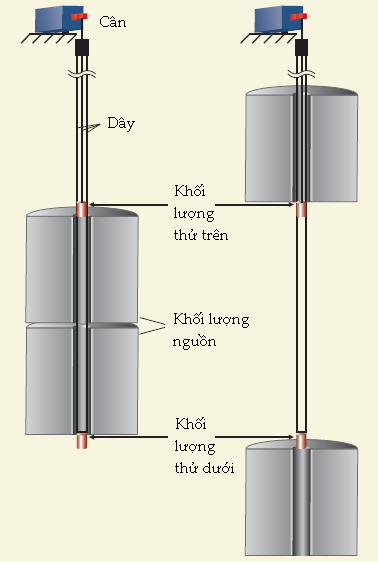
Kể từ thập niên 1990, một vài nhóm đã phát triển các thí nghiệm thành công khác ngoài cân xoắn. Trong số những thí nghiệm đầu tiên, các nhà nghiên cứu tại trường Đại học Wuppertal ở Đức đã nghĩ ra một trọng sai kế con lắc đơn, gồm hai gương kim loại treo lơ lửng bên dưới dây mảnh tạo thành một hộp cộng hưởng vi sóng treo, như minh họa trên Hình 4. Khi các khối lượng nguồn 125 kg được đặt đằng sau mỗi gương, chúng gây ra một độ lệch nhỏ của hai gương, có thể phát hiện dưới dạng sự biến thiên của tần số cộng hưởng.
Vào năm 2002, nhóm Wuppertal đã cải tiến kĩ thuật đủ để đo G với sai số theo báo cáo là 100 ppm.16 Không lâu sau đó, Harold Parks và James Faller thuộc JILA tiến hành một giải pháp tương tự, ngoại trừ là họ thay hộp cộng hưởng vi sóng bằng một hộp cộng hưởng quang học nhạy hơn và dùng bốn khối lượng nguồn thay vì hai.17 Kết quả của họ, với sai số 21 ppm, nhỏ hơn chừng 200 ppm so với giá trị CODATA 2010.
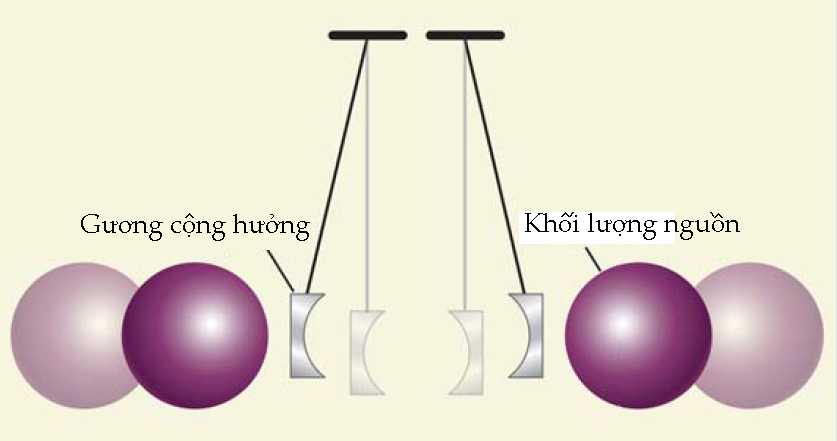
Trong một thí nghiệm ở Zurich, Stephan Schlamminger và các đồng sự đã đo G, sử dụng phương pháp cân chùm miêu tả trong Hình 5.18 Về cơ bản nó giống với phương pháp mà John Henry Poynting đã sử dụng hồi những năm 1880, phương pháp của đội Zurich là quan sát sự biến thiên trọng lượng tương đối của hai khối lượng thử treo ngay bên trên và bên dưới hai khối lượng nguồn lớn – đó là hai bình thép, mỗi bình chứa 6,5 tấn thủy ngân.
Bất chấp khối lượng nguồn lớn, tín hiệu lực hấp dẫn chỉ khoảng 8 mN. Mặc dù lực như thế là lớn so với đa số các thí nghiệm cân xoắn, nhưng nó vẫn tương đương với tín hiệu chỉ 800 mg – chừng bằng khối lượng của một giọt nước cỡ mm, chồng lên trọng lượng chừng 1,1 kg của khối lượng thử. Sai số cuối cùng, dưới 20 ppm, bị ràng buộc bởi mức vững vàng của chiếc cân thương mại tiên tiến dùng để đo. Mặc dù giá trị thu được nằm gọn trong vùng số liệu CODATA 2010, nhưng nó sai khác đáng kể, đôi khi lên tới hàng trăm phần triệu, so với hơn một nửa phép đo được tiến hành trong ba thập kỉ trước đó.
Hình 5. Trong một thí nghiệm cân chùm, một đội tại Zurich đã so sánh trọng lượng của hai khối lượng thử 1,1 kg treo ngay phía trên và ngay phía dưới các khối lượng nguồn 6,5 tấn. Khi chuyển giữa kiểu bố trí bên trái và bên phải, trọng lượng của khối lượng thử biến thiên một lượng tương đương với trọng lượng của một giọt nước cỡ milli mét. (Ảnh trích từ tài liệu tham khảo 18.)
Hướng tới tương lai
Ở trên chúng tôi vừa đề cập khả năng cải tiến các định luật Newton. Tuy nhiên, hiện nay, chưa có lí thuyết thay thế nào tỏ ra có sức thuyết phục. Khả năng cao hơn là các kết quả có sai số hệ thống lớn hơn nhiều so với sai số được ước tính của chúng. Bất chấp tinh thần làm việc nghiêm túc tại một cuộc họp tổ chức hồi tháng hai này tại Hội Hoàng gia ở Anh, không có sai số có nghĩa nào được làm sáng tỏ trong bất kì thí nghiệm nào. Mỗi nhóm đều hài lòng với kết quả của mình. Với tư cách cộng đồng, chúng ta nên làm gì vào lúc này?
Vấn đề đi tới một giá trị đáng tin cậy cho G không có khả năng được giải quyết bởi việc thu được một hoặc hai kết quả bổ sung thêm, như đã xảy ra trước đây, bởi các đội nghiên cứu độc lập. Các ước tính chính xác của G dựa trên các số đo chuẩn xác của các thông số như khối lượng, khối lượng riêng, độ dài, thời gian, cường độ dòng điện, điện áp, điện dung, và góc. Tất cả các số đo ấy phải truy nguyên đến các chuẩn quốc gia và quốc tế đã được xác thực của kilogram, mét, và giây, với sai số được đánh giá theo SI. Ngoài ra, các thí nghiệm trong tương lai phải được tiến hành trong các phòng thí nghiệm có chất lượng điều khiển nhiệt độ và điều khiển môi trường cao nhất.
Toàn bộ những yêu cầu trên hướng tới một học viện đo lường học tầm cỡ quốc gia, hoặc một phòng thí nghiệm có liên hệ chặt chẽ với một viện như thế, là nơi thích hợp nhất cho các thí nghiệm đo G trong tương lai. Tại hội nghị Hội Hoàng gia, những người tham dự đã kết luận rằng các thí nghiệm trong tương lai nên được tiến hành trong khuôn khổ hợp tác, để kinh nghiệm tập thể của chúng ta mang lại cái mới mẻ cho thiết kế, xây dựng và điều hành các thí nghiệm mới. Để thu được mục tiêu đó đòi hỏi sự hợp tác quốc tế. (Các đề xuất sẽ được thảo luận chi tiết hơn trong phiên họp lần tới diễn ra ở NIST; xem http://pml.nist.gov/bigg.)
Tuy nhiên, không một phát triển nào trong số trên giải quyết được câu hỏi gai góc mà Nhóm Công tác CODATA phải xử lí trong phiên họp 2014 sắp tới “Các giá trị được khuyến nghị của các hằng số vật lí cơ bản”: Giá trị tốt nhất và sai số tốt nhất để gán cho G là bao nhiêu?
Bài của Clive Speake và Tery Quinn đăng trên tạp chí Physics Today, tháng 7/2014
Trần Nghiêm dịch
Tham khảo:
1. P. J. Mohr, B. N. Taylor, D. B. Newell, Rev. Mod. Phys.84, 1527 (2012).
2. Special issue, Tests of the Weak Equivalence Principle,”Class. Quantum Grav. 29 (2012).
3. R. Spero et al., Phys. Rev. Lett. 44, 1645 (1980).
4. G. T. Gillies, Metrologia 24(suppl.), 1 (1987).
5. G. G. Luther, W. R. Towler, Phys. Rev. Lett. 48, 121 (1982).
6. C. H. Bagley, G. G. Luther, Phys. Rev. Lett. 78, 3047 (1997).
7. O. V. Karagioz, V. P. Izmaylov, G. T. Gillies, Grav. Cosmol.4, 239 (1998).
8. T. J. Quinn, C. C. Speake, L. M. Brown, Philos. Mag. A65, 261 (1992); C. C. Speake et al., Meas. Sci. Technol. 10,430 (1999).
9. K. Kuroda, Phys. Rev. Lett. 75, 2796 (1995).
10. W. Michaelis, H. Haars, R. Augustin, Metrologia 32, 267 (1995).
11. W. Michaelis, J. Melcher, H. Haars, Metrologia 41, L29 (2004); 42, 67 (2005).
12. T. R. Armstrong, M. P. Fitzgerald, Phys. Rev. Lett. 91, 201101 (2003).
13. J. H. Gundlach, S. M. Merkowitz, Phys. Rev. Lett. 85, 2869 (2000).
14. Z.-K. Hu, J.-Q. Guo, J. Luo, Phys. Rev. D 71, 127505 (2005); J. Luo et al., Phys. Rev. Lett. 102, 240801 (2009).
15. T. J. Quinn et al., Phys. Rev. Lett. 87, 111101 (2001); T. J. Quinn et al., Phys. Rev. Lett. 111, 101102 (2013).
16. U. Kleinevoss, “Bestimmung der Newtonschen Gravitationskonstanten G,” PhD thesis, U. Wuppertal (2002).
17. H. V. Parks, J. E. Faller, Phys. Rev. Lett. 105, 110801 (2010).
18. S. Schlamminger et al., Phys. Rev. D 74, 082001 (2006). ■







![[Chuyên đề] Boson Higgs - Hành trình nửa thế kỉ tìm kiếm](/bai-viet/images/2012/07/2-higgsboson.jpg)