- Clive Speake và Terry Quinn – Physics Today, tháng 7/2014
Ba thập niên làm thực nghiệm tỉ mỉ đã tô nên một bức tranh mờ nhạt đến bất ngờ của hằng số chi phối lực quen thuộc nhất trên Trái đất.

Lực hấp dẫn có một vị thế đặc biệt trong vật lí học. Trước tiên, nó là tương tác cơ bản duy nhất không thể mô tả được bằng thuyết lượng tử. Trong khi các lí thuyết đang thịnh hành của lực hấp dẫn – định luật hấp dẫn của Newton và thuyết tương đối rộng của Einstein – xem không gian và thời gian là những đại lượng cổ điển liên tục, thì các lí thuyết mô tả lực điện từ và các lực hạt nhân được xây dựng trên các lượng tử bảo toàn.
Lực hấp dẫn còn là lực yếu nhất trong các lực cơ bản; độ lớn của nó chỉ trở nên sánh được với độ lớn của những lực khác ở các năng lượng gần thang Planck, tức 1,22 × 1019 GeV, cao gấp chừng 15 lần so với các năng lượng đang được khảo sát tại Máy Va chạm Hadron Lớn. Sự không tương xứng đó khiến người ta nghi ngờ giá trị của mô hình chuẩn của ngành vật lí hạt, lí thuyết được cho là không tương thích với một thang năng lượng cơ bản lớn đến như vậy.
Cái không ai nghi ngờ là lực hấp dẫn, chứ không phải bất kì lực nào khác, cực kì bướng bỉnh và vẫn còn lảng tránh các phép đo chính xác. Định luật Newton, dạng thức gần đúng của thuyết tương đối rộng trong giới hạn trường hấp dẫn nhỏ và tốc độ phi tương đối tính, phát biểu rằng độ lớn F của lực hút giữa hai quả cầu khối lượng M1 và M2, cách nhau khoảng cách r, được cho bởi công thức F = GM1M2/r2. Hằng số G, chẳng có gì bất ngờ, được gọi là hằng số hấp dẫn Newton. Nó được xem là một hằng số cơ bản của tự nhiên. Nhưng đã ba thế kỉ sau khi định luật Newton được đề xuất, các thí nghiệm chưa thu được một sự nhất trí nào về giá trị của hằng số G.
Theo Ủy ban Số liệu Khoa học và Công nghệ (CODATA), cơ quan ban hành các giá trị được khuyên dùng của các hằng số cơ bản mỗi bốn năm một lần, G = 6,67384(80) × 10 – 11 kg – 1 m3 s – 2. Giá trị đó, từ năm 2010, phản ánh kết quả của gần một tá phép đo thực nghiệm đã được tiến hành trong ba thập niên qua (xem hình 1).1 Mặc dù nhiều phép đo đơn lẻ có sai số dưới 50 phần triệu (ppm), nhưng phân bố tập thể của chúng lớn hơn chừng 10 lần; cho nên có vẻ chúng ta biết G chỉ đến ba chữ số có nghĩa! Sai số biểu kiến đó rất lớn so với sai số của các hằng số vật lí khác, nhiều hằng số được biết với sai số chỉ vài phần trăm triệu (108). Hằng số Rydberg, hằng số xác định cấu trúc điện tử của các nguyên tử, được biết với sai số 4 phần nghìn tỉ (1012). (Xem bài báo của Peter Mohr và Barry Taylor, Physics Today, tháng 3/2001, trang 29.)
Thêm một cái thần bí nữa là thực tế lực hấp dẫn là lực quen thuộc nhất với chúng ta trên Trái đất này, và G có thể được xem là số đo cho biết chúng ta hiểu bao nhiêu về nó. Chẳng có gì bất ngờ khi các bất đồng giữa các xác định thực nghiệm của hằng số hấp dẫn Newton lại có thể thu hút trí tưởng tượng của đông đảo công chúng. Tại sao G lại được biết kém như vậy? Trước khi trả lời câu hỏi đó, ta hãy xét xem tại sao việc biết giá trị của G lại là quan trọng.

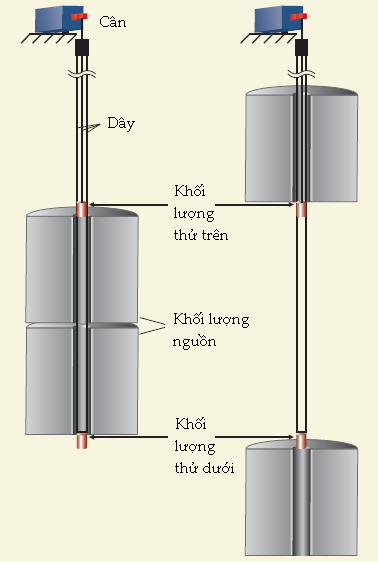
Hình 1. Các phép đo hằng số hấp dẫn Newton, G, thu được các kết quả mâu thuẫn nhau. Ở đây, kết quả của các thí nghiệm cân xoắn (nâu sẫm), con lắc (xanh lam), và cân chùm (xanh lá) đã nói trong bài được biểu diễn, cùng với vị trí và năm mà chúng được đo. Thanh sai số tương ứng với một độ lệch chuẩn; vùng tô màu sậm cho biết sai số được gán của giá trị được khuyên dùng bởi Ủy ban Số liệu Khoa học và Công nghệ vào năm 2010. (Trích từ T. J. Quinn et al., Phys. Rev. Lett. 111, 101102, 2013.)
Giá trị của G bằng bao nhiêu?
Giá trị đích thực bằng số của G có ít hệ quả đối với vật lí học. Ví dụ, các quỹ đạo hành tinh trong hệ mặt trời của chúng ta được biết là tuân theo định luật Newton và có thể được sử dụng cùng với G để ước tính khối lượng của Mặt trời. Việc hiệu chỉnh G, chẳng hạn, tăng thêm 0,05% sẽ chỉ đơn giản là làm giảm khối lượng đã ước tính của Mặt trời một lượng khoảng bằng chừng đó. Hiện nay, chúng ta chưa có mô hình nào cho cấu trúc của Mặt trời ràng buộc hữu ích khối lượng của nó ở những mức nhỏ như vậy.
Như vậy, vấn đề không phải là giá trị của hằng số G mà là khả năng của chúng ta chứng minh được nó, thật sự, là hằng số. Các lí thuyết được tin cậy ít nhiều dự đoán các vi phạm của định luật nghịch đảo bình phương của Newton ở những thang chiều dài nhỏ. Các lí thuyết khác dự đoán các vi phạm của nguyên lí tương đương – một nền tảng kinh nghiệm của thuyết tương đối rộng và, như vậy, là một nền tảng của định luật Newton – phát biểu rằng gia tốc rơi tự do của vật chất trong một trường hấp dẫn không phụ thuộc vào thành phần hóa học. Một quan điểm đang lớn mạnh cho rằng G có thể phụ thuộc vào mật độ vật chất ở cấp độ thiên văn vật lí.
Cho đến nay, cả nguyên lí tương đương2 và định luật nghịch đảo bình phương của Newton3 đều vượt qua các khảo sát thực nghiệm. Tuy nhiên, để tối đa hóa độ nhạy và giảm nhẹ gánh nặng cho ngành đo lường học, các phép kiểm tra thực nghiệm đó được thiết kế khéo léo để đưa ra một tín hiệu nhỏ xíu chỉ khi nào tự nhiên không hành xử theo cách mà các nhà thực nghiệm muốn thấy. Các phép đo thực tế của G phải xem xét toàn bộ các đại lượng có liên quan theo đơn vị vật lí và phải gắn liền với các tiến bộ đo lường học. Các số đo không nhất quán của G có thể báo hiệu rằng chúng ta chưa hiểu cơ sở đo lường của việc đo các lực yếu, cái hóa ra có thể hàm ý rằng các kiểm tra thực nghiệm xác thực định luật nghịch đảo bình phương và tính vạn vật của sự rơi tự do có chỗ nào đó còn sơ hở. Một phát triển như thế sẽ đưa đến một tình huống thú vị, cái có thể lí giải tại sao người ta lại quá lao tâm khổ tứ vì một thứ tầm thường và cực nhọc như thế.






![[Chuyên đề] Boson Higgs - Hành trình nửa thế kỉ tìm kiếm](/bai-viet/images/2012/07/2-higgsboson.jpg)












![[Sách] Công nghệ tính toán thời cổ đại](/bai-viet/images/stories/hiepkhachquay3/cntt1.bmp)


