Bối cảnh lịch sử
Khái niệm một hằng số cơ bản không tồn tại vào thời của Isaac Newton. Ông không đưa ra dứt khoát một hằng số trong định luật của ông; thay vậy G được hàm ý như thể giá trị của nó bằng 1. Cho đến năm 1873 thì Alfred Cornu và Baptistin Baille mới đưa ra dứt khoát một kí hiệu cho hằng số kết hợp hấp dẫn, cái họ gọi là f. Hằng số hấp dẫn đã không có kí hiệu G hiện nay của nó mãi cho đến thập niên 1890.
Sự phát triển khái niệm các hằng số cơ bản ban đầu vốn gắn liền với sự phát triển các hệ đơn vị vật lí. David Newell, trong bài báo của ông ở trang 35 (tạp chí Physics Today, tháng 7/2014), mô tả làm thế nào, bắt đầu vào năm 2018, các đơn vị SI sẽ có khả năng được xây dựng trên các giá trị số cố định của bảy hằng số cơ bản, trong đó có tốc độ ánh sáng và hằng số Planck. Hằng số Planck sẽ xuất hiện trong định nghĩa mới của kilogram.
Vậy sao chúng ta không thể định nghĩa kilogram theo G? Ví dụ, “kilogram là đơn vị khối lượng, và độ lớn của nó được thiết lập bởi việc cố định giá trị số của G là 6,67384 × 10- 11 kg – 1 m3s – 2.” Trên lí thuyết, định nghĩa đó sẽ hoạt động tốt, nhưng trên thực tế, mọi phép đo khối lượng của một vật theo lực hút hấp dẫn của nó với vật khác sẽ chỉ có độ chính xác vài trăm phần triệu – nhỏ hơn khoảng bốn bậc độ lớn so với chuẩn cần thiết trong đo lường tiên tiến và có thể thu được từ một định nghĩa dựa trên hằng số Planck. Đơn giản vì lực hấp dẫn quá yếu ở cấp bậc phòng thí nghiệm: Lực hấp dẫn giữa một cặp quả cầu bằng đồng 1 kg đặt chạm nhau xấp xỉ bằng 10 – 8 N, khoảng bằng một phần nghìn của một phần triệu của trọng lượng của mỗi quả cầu.
Để tiến hành một phép đo cho dù là thô sơ của G với một cặp quả cầu như thế, người ta phải tìm một cách triệt tiêu trọng lực át trội hướng xuống mà không làm nhiễu độ nhạy của các quả cầu đối với lực hấp dẫn tương hỗ giữa chúng. Lúc gần cuối thế kỉ 18, John Michell đã khám phá ra một cách đẹp đẽ để làm công việc đó: Bằng cách đặt hai quả cầu – cái gọi là khối lượng thử – tại hai đầu đối diện của một thanh đòn nằm ngang được treo bằng một sợi dây đồng, như minh họa trên hình 2a, một quả cầu có thể trung hòa lực hút hướng xuống của Trái đất còn quả cầu kia cho hệ tự do quay trong mặt phẳng nằm ngang.
Hệ vật của ông là một tương đương chuyển động quay của một vật nặng treo trên một lò xo; giả sử sợi dây hành xử đàn hồi, hai quả cầu lớn hơn được bố trí thích hợp (khối lượng nguồn) sẽ làm cho cán cân nghiêng đi một góc phụ thuộc vào lực hấp dẫn và hằng số moment động lượng của sợi dây, k. Hằng số moment động lượng có thể được xác định bằng cách đo chu kì dao động tự nhiên T0 của hệ vật xoắn và sử dụng k = I(2p/T0)2, trong đó I là moment quán tính. Michell đã phát minh ra cân xoắn.
Chẳng phải chờ đến khi Michell qua đời thì thiết bị của ông mới được đưa vào sử dụng: Henry Cavendish đã sử dụng nó để “cân” Trái đất bằng cách so sánh lực hút hấp dẫn giữa khối lượng thử và khối lượng nguồn với lực hút hấp dẫn giữa khối lượng nguồn và Trái đất. Công bố năm 1798 của Cavendish mô tả hết sức tường tận thí nghiệm chính xác đầu tiên trong vật lí học. Cân xoắn của ông là một trong những thiết bị vật lí có ý nghĩa nhất từng được phát minh. Trong một tài liệu biên soạn các công trình đã công bố về các phép đo G, Georges Gillies liệt kê khoảng 350 bài báo, hầu như toàn bộ đều nói công trình được thực hiện với cân xoắn4. Trong số chừng một tá thí nghiệm được sử dụng cho đánh giá CODATA mới nhất, chỉ trừ ba thí nghiệm, còn lại đều được thực hiện với cân xoắn.
Nếu như Cavendish có dịp đặt chân vào bất kì phòng thí nghiệm cân xoắn hiện đại nào, ông sẽ lập tức nhận biết cái gì đang diễn ra. Mặc dù các hệ vật cân xoắn ngày nay được bảo vệ bởi buồng chân không, chứ không phải những cái hộp gỗ đã dùng trong thí nghiệm Cavendish, nhưng nguyên lí cơ bản vẫn là tách lực hấp dẫn nhỏ giữa các vật nặng cỡ phòng thí nghiệm với Trái đất to lớn, còn lực hút hướng xuống vẫn như cũ.
Tuy nhiên, Cavendish sẽ bất ngờ thấy rằng sau nhiều năm trôi qua như thế, độ chính xác của phép đo chỉ được cải thiện một cách khiêm tốn – hầu như không có nhiều tiến bộ như đối với mỗi đại lượng vật lí khác. Ngày nay chúng ta ước tính độ chuẩn xác của phép đo Cavendish là chừng 1%, không tệ lắm so với phổ phân bố cho giá trị CODATA hiện nay. Để hiểu làm thế nào chúng ta đạt tới tình hình này, trước tiên hãy xét xem cái gì thật sự đã thay đổi trong thiết kế và hoạt động của cân xoắn kể từ thời Cavendish.
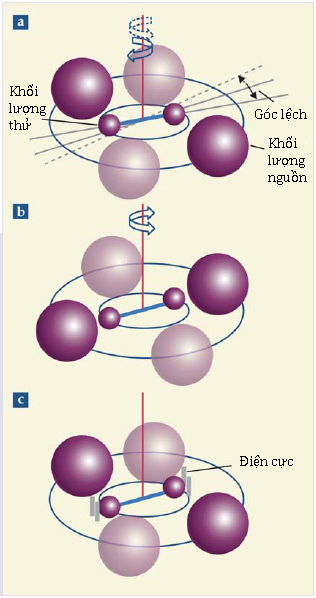
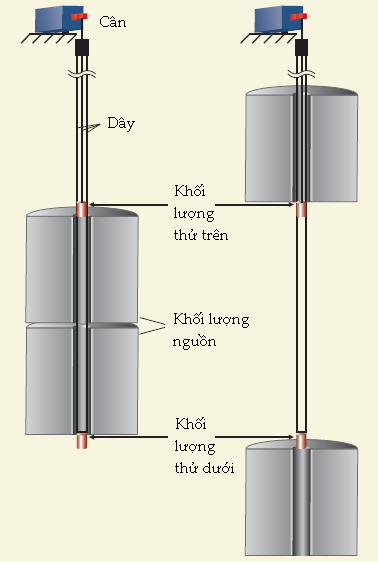
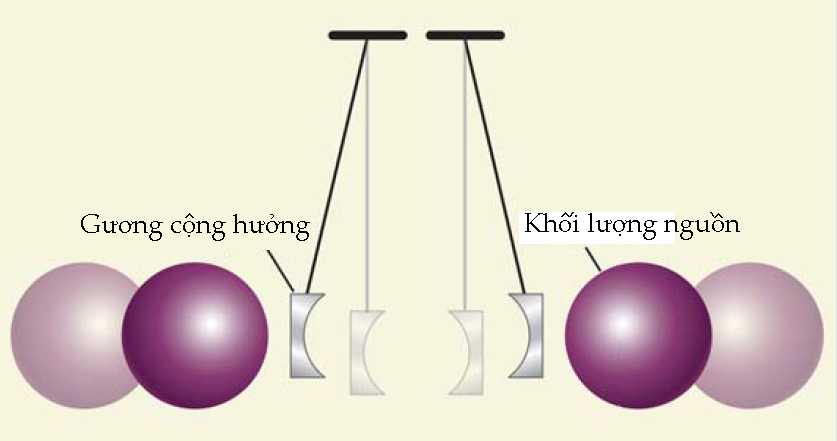
Hình 2. Bộ phận trung tâm của một thí nghiệm cân xoắn là hai khối lượng thử nằm cân bằng trên một thanh đòn được treo bởi một dây kim loại mảnh. (a) Trong bố trí ban đầu do John Michell nghĩ ra và sau này được Henry Cavendish sử dụng, hai khối lượng nguồn lớn được bố trí để tác dụng một lực hấp dẫn làm cho cân xoắn quay lệch một góc nhỏ. Kiểu bố trí hai khối lượng nguồn minh họa bằng màu đậm mang lại góc xoắn theo chiều kim đồng hồ, còn bố trí minh họa bằng màu nhạt cho góc xoắn ngược chiều kim đồng hồ. (b) Trong cái gọi là thí nghiệm thời-gian-lúc-lắc, G được tính từ độ biến thiên chu kì dao động khi hai khối lượng nguồn được bố trí lại giữa nằm dọc (hai quả cầu màu đậm) và nằm vuông góc (hai quả cầu màu nhạt) với trục nối hai khối lượng thử đang nằm yên. (c) Trong kiểu bố trí thứ ba, kĩ thuật cơ cấu điều khiển phụ tĩnh điện, lực hấp dẫn được tính từ điện áp phải đặt vào hai điện cực để giữ cho hệ vật thử nằm tại chỗ. Trong cả ba kiểu sắp xếp, người ta phải tính sự kết hợp hấp dẫn giữa các khối lượng nguồn và toàn bộ hệ vật cân xoắn.







![[Chuyên đề] Boson Higgs - Hành trình nửa thế kỉ tìm kiếm](/bai-viet/images/2012/07/2-higgsboson.jpg)