Cảm hứng...
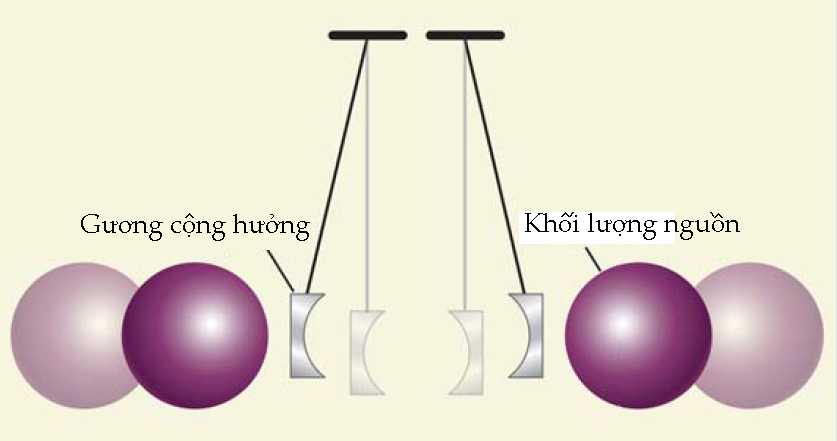
Một trong những cải tiến quan trọng nhất đối với phương pháp Cavendish được thực hiện vào năm 1894 bởi Charles Boys, người nhận ra rằng dụng cụ có độ nhạy tốt nhất khi sử dụng sợi dây mảnh nhất. Đó là bởi vì hằng số moment động lượng tăng theo lũy thừa bốn của đường kính dây, còn tải trọng mà dây có thể chịu được tăng theo đường kính bình phương. Mặc dù dây mỏng hơn thì đòi hỏi khối lượng thử nhẹ hơn, nhưng lực hấp dẫn giảm được bù lại nhiều hơn bởi sự tăng khả năng đàn hồi trong dây; kết quả là một góc lệch lớn hơn, dễ đo hơn. Hầu như toàn bộ các thí nghiệm cân xoắn kể từ thời của Boys đều sử dụng một sợi dây mảnh với một hệ vật treo nhiều nhất là vài gram. Trong bố trí ban đầu của Cavendish, khối lượng thử là những quả cầu chì lớn hơn nhiều, mỗi quả cân nặng chừng 750 gram.
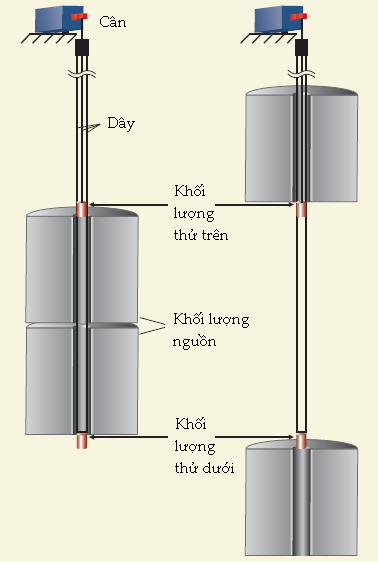
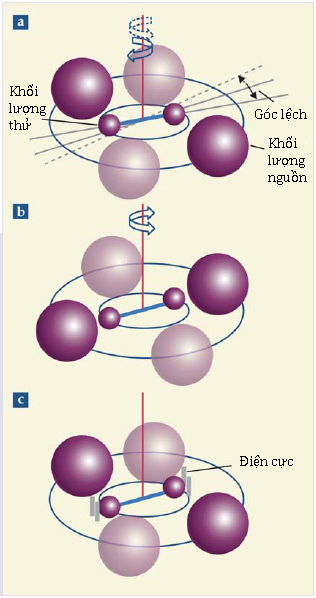
Tiến bộ lớn tiếp theo được thực hiện vào năm 1895 bởi Loránd Eötvös, ông đã đưa ra cái gọi là phương pháp thời gian đong đưa. Theo phương pháp đó, chu kì dao động tự do của hệ cân xoắn được đo với các khối lượng nguồn ban đầu được bố trí dọc, sau đó theo đường chéo, với trục khối lượng thử (xem hình 2b). Trong kiểu bố trí ban đầu đó, lực hút hấp dẫn giữa khối lượng nguồn và khối lượng thử làm giảm chu kì; trong kiểu bố trí thứ hai, nó làm tăng chu kì. Ưu điểm của phương pháp này là một biến thiên nhỏ của chu kì dao động thì dễ đo hơn một biến thiên nhỏ của góc lệch.
Các kĩ thuật tiếp tục được cải tiến trong nửa thế kỉ sau đó, nhưng phương pháp thì vẫn như cũ. Vào thập niên 1970, Gabriel Luther thuộc Cục Tiêu chuẩn Quốc gia Mĩ (NBS, nay là NIST) ở Gaithersburg, Maryland, và William Towler thuộc trường Đại học Virginia đã sử dụng phương pháp thời gian đong đưa để đo G với sai số 70 ppm.5 Kết quả đó là cơ sở chính cho giá trị được thông qua trong phiên bản CODATA 1986 của các hằng số cơ bản. Sau đó, Charles Bagley và Luther, tại Phòng thí nghiệm quốc gia Los Alamos, đã lặp lại thí nghiệm NBS sử dụng một cách sắp xếp khác của các khối lượng nguồn.6 Cùng khoảng thời gian đó, một đội tại Công ti Nghiên cứu và Phát triển Tribotech ở Moscow đã tiến hành một loạt phép đo thời gian đong đưa, sử dụng các dây đa dạng và các sắp xếp đa dạng của khối lượng nguồn và khối lượng thử.7
Các nhà đo lường học khi ấy có mọi lí do để nghĩ rằng một sai số 10 ppm đã nằm trong tầm tay. Các nỗ lực cải thiện các ước tính của G bằng cách sử dụng các khối lượng cực lớn ví dụ như núi non và hồ tự nhiên đã thất bại; mặc dù các tín hiệu hấp dẫn là lớn hơn, nhưng sai số, chẳng hạn, của phân bố khối lượng bên trong ngọn núi và hình dạng của đáy hồ, cũng lớn hơn. Tuy nhiên, có ít lí do để nghĩ rằng giá trị CODATA là sai sót.
... và mồ hôi nước mắt
Vào thập niên 1990, hai phát triển đã khiến người ta nghi ngờ giá trị CODATA 1986. Thứ nhất là vấn đề đàn hồi phụ thuộc thời gian, thực tế thì dây kim loại trong cân xoắn không hành xử giống như một lò xo lí tưởng. Cách tiếp cận thông thường trong ngành khoa học vật liệu là xem một sợi dây như vậy là vật liệu Maxwell – về cơ bản, một lò xo bị nén vừa có thành phần đàn hồi vừa có thành phần nhớt. Mô hình Maxwell dự đoán một hậu hiệu ứng đàn hồi phụ thuộc thời gian, như Cavendish quan sát, trong đó lò xo cần một khoảng thời gian hữu hạn để hồi phục sau khi lực nén thôi tác dụng.
Vào đầu thập niên 1990, chúng tôi và các cộng sự của chúng tôi phát hiện thấy mô hình Maxwell thông thường không giải thích được trọn vẹn hành trạng của cân xoắn. Đặc biệt, lí thuyết và các thí nghiệm của chúng tôi cho thấy các hệ xoắn không có một mà có nhiều thời gian hồi phục đặc trưng; sự nén trông mạnh hơn lên khi chu kì kéo dài hơn, và thời gian hồi phục về cơ bản là trở nên vô hạn.8 Hiệu ứng xuất hiện rõ nét ở các chu kì biến thiên từ dưới một giây đến dài hơn 10 phút. Chúng tôi đã có thể liên hệ hậu hiệu ứng đàn hồi phụ thuộc thời gian với sự có mặt của cái gọi là nhiễu 1/f phát sinh từ sự chuyển động của các biến vị trong dây kim loại.
Kazuaki Kuroda lúc ấy suy luận rằng hành trạng đàn hồi phụ thuộc thời gian sẽ làm các phép đo thời gian đong đưa chịu sai số tỉ lệ nghịch với hệ số phẩm chất Q, một đại lượng cho biết cân xoắn gần giống đến mức nào với một lò xo đàn hồi lí tưởng.9 Ông đã tính các hiệu chỉnh cho nhiều phép đo cân xoắn cổ điển; ông đã hiệu đính toàn bộ chúng, trong đa số trường hợp là giảm vài phần chục của một phần trăm. Các phép đo NBS mà giá trị CODATA 1986 xây dựng trên đó được hiệu chỉnh xuống khoảng 50 ppm sau các thí nghiệm xác thực bởi Bagley và Luther, họ sử dụng hai dây có Q chênh lệch nhau nhiều.
Vào năm 1996, một phát triển thứ hai đã làm lung lay giá trị CODATA: việc công bố một kết quả của Winfried Michaelis và các cộng sự tại Physikalisch-Technische Bundesanstalt (PTB) ở Braunschweig, Đức.10 Michaelis và các cộng sự của ông đã sử dụng một cân xoắn mới lạ trong đó các khối lượng thử được cho nổi lơ lửng trong bể thủy ngân chứ không treo bằng dây. Thay vì đo góc lệch hay độ biến thiên chu kì do lực hút hấp dẫn của các khối lượng nguồn ở gần, các nhà nghiên cứu sử dụng điều khiển hồi tiếp để tác dụng một moment tĩnh điện vừa đủ mạnh để giữ các khối lượng thử tại chỗ (xem hình 2c). Khi đó, giá trị của điện áp đặt vào có thể được dùng để suy ra G. Bởi vì không có dây xoắn, cho nên không có hiệu ứng đàn hồi phụ thuộc thời gian.

Hình 3. Hai vòng xoắn trên cân xoắn. (a) Một nhóm tại trường Đại học Washington sử dụng tấm phẳng có thể nhìn thấy ở giữa, thay cho sắp xếp thanh ngắn truyền thống, làm khối lượng thử trong phép đo cân xoắn của hằng số hấp dẫn G. (Một đồng xu nằm ở góc dưới bên trái chuyển tải cân xoắn.) Trong một bố trí như vậy, giá trị được suy luận ra của G hầu như độc lập hoàn toàn với phân bố khối lượng của các khối lượng thử. (Ảnh của Jens Gundlach) (b) Các nhà nghiên cứu tại trường Đại học Khoa học và Kĩ thuật Hoa Trung ở Vũ Hán, Trung Quốc, sử dụng một phiến thạch anh làm khối lượng thử, mang lại các ưu điểm đo lường học tương tự như trên. Các khối lượng nguồn được bố trí theo cái gọi là cấu hình thời gian đong đưa, đã được mô tả chi tiết trên hình 2b. (Ảnh của Jun Luo)
Ước tính G của đội PTB lệch với giá trị CODATA được chấp nhận lúc ấy khoảng chừng 0,7%, sai số ước tính của thí nghiệm là khoảng 80 ppm và sai số CODATA là 127 ppm. Một vài nhóm khác, trong đó có một nhóm do một người chúng tôi đứng đầu (Quinn) tại Cục Cân Đo Quốc tế (BIPM) – ngôi nhà của nguyên mẫu quốc tế kilogram – đã đáp lại bằng cách bắt tay vào các thí nghiệm G của riêng họ.
Nhóm BIPM phát hiện thấy kĩ thuật điều khiển phụ có thể chịu sai số đáng kể nếu bộ tĩnh điện được chế tạo ở một tần số khác với tần số mà nó được sử dụng. Không bao lâu sau đó, người còn lại trong chúng tôi (Speake) đã đề xuất một nguồn sai số khả dĩ khác trong thí nghiệm PTB: Số hạng điện dung tiết diện trong chế tạo tĩnh điện đã bị bỏ qua. Các nghiên cứu sau đó tại PTB11 xác nhận rằng sai sót thật sự đã làm các phép đo ước tính giá trị của G cao hơn khoảng 0,7%.
Kể từ đó, các kĩ thuật điều khiển phụ đã được sử dụng để tiến hành các phép đo chính xác nhất của G. Vào năm 2003, Tim Armstrong và Mark Fitzgerald thuộc Phòng thí nghiệm Tiêu chuẩn Đo lường New Zealand đã sử dụng phương pháp trên để tính G với sai số 40 ppm.12 Các nhà nghiên cứu đã sử dụng gia tốc phi quán tính của cân xoắn gắn xoay được, thay vì các phép đo điện dung, để chế tạo bộ phận tĩnh điện của họ. Nhờ đó, họ né tránh được các vấn đề mà các công nhân PTB đã gặp.






![[Chuyên đề] Boson Higgs - Hành trình nửa thế kỉ tìm kiếm](/bai-viet/images/2012/07/2-higgsboson.jpg)