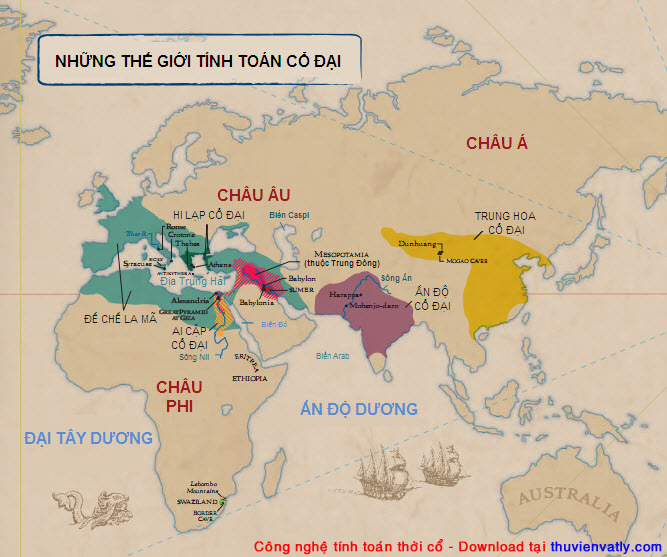
CHƯƠNG NĂM
TRUNG HOA CỔ ĐẠI
Người Trung Hoa cổ đại là những nhà toán học tiên tiến. Họ đã phát triển cơ sở cho hệ đếm thập phân và phát minh ra dụng cụ tính toán tự động đầu tiên, cái bàn tính. Có lẽ họ còn khám phá ra các ý tưởng hình học trước khi người Hi Lạp biến những ý tưởng đó thành nổi tiếng.
SỐ VẠCH VÀ BẢNG TÍNH
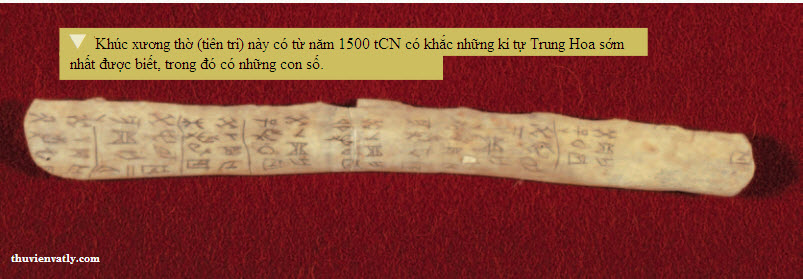
Theo tiến trình lịch sử, người Trung Quốc đã viết nhiều loại chữ số khác nhau. Từ năm 1500 tCN, những thầy tế cổ đại đã khắc một loại chữ số vào vỏ và xương động vật. Họ sử dụng những vật này trong những dịp tế lễ để nhìn thấu tới tương lai. Các câu khắc ghi lại số lượng động vật hiến tế, số lượng tù binh trong chiến tranh, số động vật săn được, và vân vân. Đây là những chữ số Trung Hoa sớm nhất được ghi nhận. Các nét thẳng và nét cong tạo nên kí tự cho các số từ 1 đến 9. Những số này kết hợp với các kí tự cho 10, 100, và 1000 để tạo ra những con số lớn hơn.
Bắt đầu vào khoảng năm 400 tCN, các chữ số vạch đã được sử dụng trong hệ đếm giá trị-vị trí. Những chữ số này là những vạch ngắn. Các số từ 1 đến 5 được biểu diễn bằng một đến năm vạch. Những hình dạng chữ T được dùng để biểu diễn những số từ 6 đến 9. Chữ số ở bên phải biểu diễn cho hàng đơn vị, chữ số tiếp theo phía bên trái biểu diễn hàng chục, chữ số tiếp theo cho hàng trăm, và cứ thế.
Những chữ số vạch có khả năng có nguồn gốc từ những que đếm. Người học trò và các học giả ở Trung Hoa cổ đại thực hiện các phép tính bằng que trên bảng tính. Bảng tính được làm bằng gỗ và được chia thành các cột hoặc ô vuông. Người ta sử dụng các que đếm màu đỏ và màu đen cho các số dương và số âm. Mỗi que đếm dài khoảng 10 cm. Một bộ đầy đủ gồm cả thảy 271 que.
Các que được đặt vào các ô của bảng đếm, với mỗi cột từ phải sang trái biểu diễn hàng đơn vị, hàng chục, hàng trăm, hàng nghìn, và vân vân. Các que không được đặt cẩn thận lên bảng sẽ gây ra sự lộn xộn. Vì thế, vào những năm 200 sCN, các số que đếm sử dụng các vạch đặt theo hướng xen kẽ. Chữ số hàng đơn vị, ở bên phải, các vạch đứng. Cột hàng chục thì sử dụng vạch ngang, rồi vạch đứng cho cột hàng trăm, và tiếp tục lặp lại như vậy. Một ô trống là biểu diễn số 0. Vào khoảng năm 700, khi người Ấn Độ bắt đầu sử dụng một kí tự cho số 0, việc sử dụng kí tự đó cũng được truyền bá vào Trung Quốc.

CỬU CHƯƠNG
Jiuzhang suanshu, hay Cửu chương Thủ tục Toán học, là tác phẩm toán học Trung Hoa cổ đại nổi tiếng nhất. Nó ra đời vào khoảng giữa năm 200 tCN và năm 50 sCN. Tác phẩm cổ đại này gồm 246 bài toán. Nó là một quyển sách giáo khoa cần thiết cho học trò học toán từ thế kỉ thứ 7 đến thế kỉ 12 sau Công nguyên.
Các bài toán trong Cửu chương thể hiện tính đa dạng của những kĩ năng toán học mà người Trung Hoa đã đúc kết được. Bộ bài tập thứ nhất liên quan đến trắc địa. Một bộ bài toán khác yêu cầu học trò phải tìm tỉ lệ và tỉ lệ phần trăm cho sản phẩm buôn bán. Những bộ bài toán khác liên quan đến các vấn đề kĩ thuật, thuế, và tính toán chi phí. Nhiều bài toán trong Cửu chương đòi hỏi những phép tính phức tạp với các phân số.
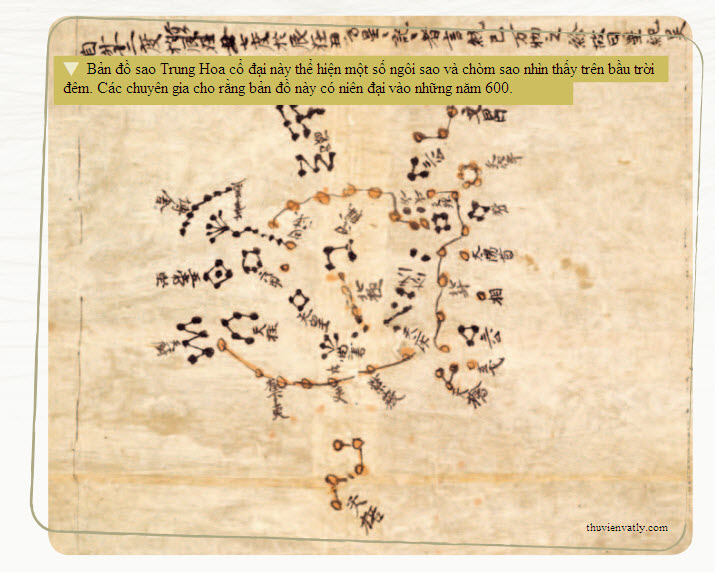
THIÊN VĂN HỌC TRONG VĂN TỰ CỔ
Giống như những nền văn hóa cổ đại khác, người Trung Hoa cổ đại có hứng thú với sự chuyển động của Mặt trời, Mặt trăng, các vì sao, và những thiên thể khác. Họ thận trọng theo dõi những biến chuyển của bầu trời đêm. Ghi chép của người Trung Quốc về nhật thực và nguyệt thực có từ những năm 1200 tCN. Đó là một số trong những bản ghi nhật nguyệt thực cổ nhất hiện có.
Thiên văn học là tâm điểm của một văn tự Trung Hoa nổi tiếng. Zhoubi Suanjing là một trong “mười tác phẩm toán kinh điển”, cùng với Cửu chương. Văn tự trên ra đời vào khoảng giữa năm 100 tCN và năm 100 sCN, mặc dù người ta tin rằng chất liệu của nó có tuổi còn lớn hơn. Phần lớn tác phẩm trên tập trung vào việc đo đạc vị trí và sự chuyển động của các vật thể trên bầu trời với một cột đồng hồ mặt trời. Tựa đề của nó có nghĩa là “Hướng dẫn đo bóng đời Chu”.
Một phần khác của tài liệu trên nói về chiều dài cạnh và diện tích của tam giác vuông. Trong nhiều năm, văn tự này đã được tôn vinh là đã chứng minh chiều dài các cạnh của một tam giác vuông liên hệ với nhau như thế nào. Trong hình học, công thức này được gọi là định lí Pythagoras. (Một định lí là một phát biểu đã được chứng minh) Nó mang tên nhà triết học Hi Lạp cổ đại Pythagoras. Nhưng chất liệu của tập sách này được cho là có tuổi lớn hơn Pythagoras. Vậy định lí Pythagoras thật ra là một khám phá của người Trung Quốc hay sao? Các học giả hiện đại không dám chắc. Có khả năng văn tự trên đã bị dịch sai bởi những nhà dịch thuật hoặc theo năm tháng những nhà toán học khác đã bổ sung thêm phần bình chú.

TÍNH SỐ PI
Một số nhà toán học Trung Hoa đã tìm thấy những giá trị chính xác hết sức ấn tượng của số pi. Vào năm 264, Liu Hui đã sử dụng một đa giác (một hình khép kín với bất kì số cạnh thẳng nào) để phỏng lại hình dạng của một vòng tròn lớn. Đa giác của ông có 3072 cạnh. Ông biết làm thế nào tìm ra chu vi và bán kính của hình đó, nên ông có thể giải tìm ra pi. Ông tìm được pi bằng 3,14159. Giá trị đúng của số pi có phần thập phân vô hạn, nhưng khi làm tròn đến năm chữ số thập phân, thì giá trị này là cực kì chính xác.
Hai nhà toán học cha con còn tìm ra một giá trị chính xác hơn nữa vào khoảng năm 480. Tsu Ch'ung-Chih và Tsu Keng-Chih tìm được giá trị của pi vào khoảng 355 ¸ 113. Giá trị đó bằng 3,1415929203 khi làm tròn đến mười chữ số thập phân. Nó vẫn là giá trị chính xác nhất của số pi trong khoảng 1200 năm trời.
Công nghệ tính toán thời cổ
Michael Woods & Mary B. Woods
Trần Nghiêm dịch

















![[Sách] Công nghệ tính toán thời cổ đại](/bai-viet/images/stories/hiepkhachquay3/cntt1.bmp)