CHƯƠNG CUỐI
SAU THỜI CỔ ĐẠI
Các xã hội cổ đại phát triển thịnh vượng rồi lụi tàn. Thường thì những nhóm non yếu về chính trị hoặc yếu kém về kinh tế bị những nhóm khác xâm chiếm, nô dịch. Nhưng cho dù một nền văn hóa đã diệt vong, thì công nghệ của nó vẫn còn đó. Những nhóm người đi xâm lược xây dựng xã hội trên kiến thức của nhóm người bị xâm lược để tiếp tục phát triển công nghệ.
Tuy nhiên, điều đó không phải lúc nào cũng đúng. Sau khi đế quốc La Mã rơi vào tay kẻ xâm lược vào năm 476, toàn cõi châu Âu đã bước vào một thời kì gọi là Thời kì Trung Cổ (khoảng năm 500 đến 1500). Thời Trung Cổ thỉnh thoảng còn được gọi là Kỉ nguyên Tăm tối, vì nghệ thuật, văn hóa và học thuật ở châu Âu trong những năm tháng này bị suy yếu đến mức tối thiểu. Một số người thợ thủ công đã biết hoặc cải tiến dựa trên công nghệ cổ. Khoảng năm 900, chữ số Hindu-Arab đã du nhập vào châu Âu. Chúng thay thế chữ số La Mã trong công dụng hàng ngày, lập nên giai đoạn tính toán dễ dàng hơn với hệ đếm thập phân Ấn Độ.
Những nền văn hóa thuộc những vùng miền khác của thế giới tiếp tục phát triển kiến thức của họ về sự tính toán và toán học trong thời Trung Cổ. Người Maya xây dựng xã hội phồn vinh ở Trung Mĩ. Ở Trung Hoa, nhà Tống đã thúc đẩy nhiều tiến bộ văn minh. Người Inca ở Peru đã xây dựng một đế quốc hùng mạnh trên vùng núi non.
Sau đó, trong một thời kì gọi là thời Phục hưng (1300 – 1600), người châu Âu đã khám phá lại công nghệ Hi Lạp và La Mã cổ đại. Vào những năm 1400, các học giả đá khám phá lại những tập sách toán cổ cùng những cuộn tài liệu lưu giữ trong thư viện và tu viện thuộc những đế quốc châu Âu trước đó. Sự phát minh trở lại của nền toán học tiên tiến có từ thời cổ đại đã làm nền toán học hiện đại phát triển vượt bậc.
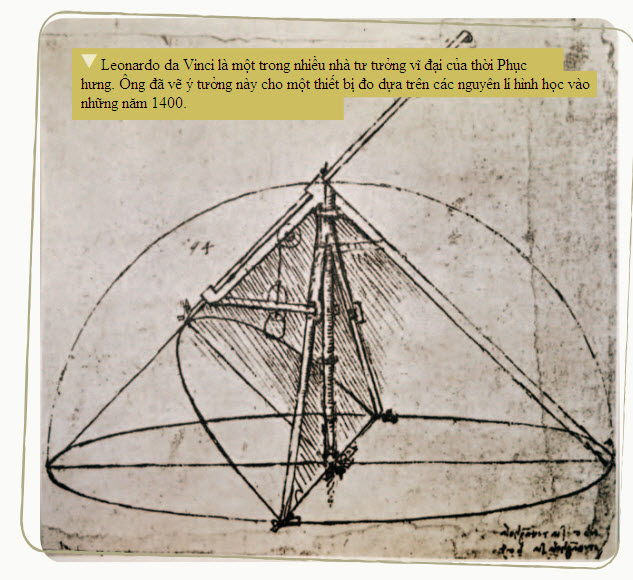
Ngoài ra, sự thám hiểm toàn cầu đã mang đến sự truyền bá công nghệ. Người châu Âu đã đi thám hiểm và định cư ở châu Mĩ vào thế kỉ thứ 16 và 17. Các thuộc địa châu Âu ở châu Á và châu Phi cũng mang kiến thức thuộc những nền văn hóa khác nhau lại hòa nhập với nhau. Ở nhiều nơi, chế độ thuộc địa tàn khốc – hay chế độ thực dân – đã khiến kiến thức và công nghệ của những nhóm người yếu hơn bị đi vào quên lãng. Đó là trường hợp khi người Tây Ban Nha xâm chiếm Inca ở Nam Mĩ. Tuy nhiên, khi sự linh hoạt toàn cầu và truyền thông phát triển, thì sự truyền bá những ý tưởng toán học cũng lan rộng theo.
CÔNG NGHỆ TRỤ VỮNG VỚI THỜI GIAN
Trong thời hiện đại, phần lớn công nghệ tính toán của chúng ta là giữ nguyên những kĩ thuật cổ đại. Hệ thống đếm hiện đại của chúng ta dựa trên cơ số 10. Nhưng bạn cũng có thể tìm thấy bằng chứng của hệ đếm Mesopotamia, hệ đếm cơ số 60, trong cuộc sống hàng ngày. Chúng ta vẫn dùng 60 làm cơ số đo cho thời gian. Một phút có 60 giây. Một giờ có 60 phút. Độ (đơn vị đo góc) cũng được chia ra theo 60. Một vòng tròn chứa 360 độ, bằng 60 x 6.
Cân đòn là một thí dụ khác của công nghệ tính toán Babylon cổ đại còn trụ vững theo thời gian. Những cái cân này vẫn có ích cho nhiều mục đích khác nhau. Những chiếc cân dùng trong phòng mạch của bác sĩ thường là cân đòn. Đối trọng trượt ở phía trên cân cân bằng với trọng lượng cơ thể của bạn.
Ở một số nơi, thương nhân và một số người vẫn còn dùng bàn tính. Theo tiến trình thời gian và truyền bá khắp toàn cầu, những chiếc máy vi tính đơn giản này vẫn có sức sống riêng của chúng trước công nghệ tiên tiến. Trung Quốc không phải là nền văn hóa duy nhất phát triển một máy tính thuộc loại như thế. Những phiên bản khác của bàn tính được sử dụng ở Sumeria cổ đại, Hi Lạp cổ đại, và La Mã cổ đại, và tiến vào thời hiện đại, ở nước Nga và Nhật Bản. Quân đội Mĩ đã kiểm tra công dụng của chiếc bàn tính kiểu Nhật hồi năm 1946. Họ đã dùng bàn tính và máy tính bằng điện mới toanh khi ấy đấu với nhau về tốc độ và độ chính xác. Mỗi chiếc máy có một người điều khiển am tường để giải những bài toán có sử dụng phép cộng, trừ, nhân và chia. Chiếc bàn tính đã giành phần thắng với tỉ số áp đảo 4 trên 1!
XÂY DỰNG TRÊN NHỮNG Ý TƯỞNG CỔ ĐẠI
Tất nhiên, theo thời gian, người ta đã cải tiến nhiều loại công nghệ tính toán. Một thí dụ như vậy là lịch hiện đại của chúng ta. Sau khi Julius Caesar phê chuẩn lịch Julian vào năm 45 tCN, người dân ở nhiều vùng trên thế giới đã sử dụng nó trong hơn 1500 năm trời. Nhưng theo thời gian, sai số 11-phút-trên-năm trong bộ lịch đã góp đủ thành đơn vị ngày. Những ngày lễ tết không còn diễn ra đúng thời điểm trong năm nữa.
Một bộ lịch mới hơn, gọi là lịch Gregory, gần chính xác như năm mặt trời. Bộ lịch này chọn mốc trước và sau Công nguyên dựa trên ngày sinh của Chúa Jesus. Một tu sĩ đã nghĩ ra hệ đếm năm này vào năm 525, B.C [trước Công nguyên] trong tiếng Anh là viết tắt của “Before Christ” [Trước Chúa], A.D [sau Công nguyên] trong tiếng Anh là viết tắt của từ Latin anno Domini, nghĩa là “trong năm thiên chúa của chúng ta”.
Vào năm 1582, Giáo hoàng Gregory XIII, người đứng đầu Giáo hội Thiên chúa La Mã, đã đưa 10 ngày ra khỏi lịch. Ông cho thông qua lịch Gregory. Đây là bộ lịch vẫn sử dụng ở đa số các nước.
Dặm kế của Vitruvius cũng khích lệ nhiều cải tiến. Người La Mã chưa bao giờ sử dụng cái dặm kế mà Vitruvius mô tả. Nó bị lãng quên trong chừng 1300 năm. Sau đó, thiết kế của ông đã được khám phá lại vào năm 1414. Kĩ sư vĩ đại người Italy Leonardo da Vinci (1452–1519) sau này đã thử chế tạo từ sự mô tả trong tài liệu của Vitruvius, nhưng ông làm nó hoạt động được. Nhờ những tiến bộ trong công nghệ cơ giới, vào giữa thế kỉ 19, các nhà phát minh đã chế tạo ra kilomet kế thuộc loại được sử dụng trong xuyên suốt thế kỉ thứ 20. Những cái kilomet kế này sử dụng nhiều bánh răng. Mỗi bánh răng quay một mặt đồng hồ số sao cho người lái xe có thể nhìn biết anh ta hoặc cô ta đã đi được bao xa.
Vào thế kỉ thứ 17, các nhà toán học đã nêu ra nhiều ý tưởng mới dựa trên những khái niệm cổ. Năm 1619, nhà toán học người Pháp René Descartes đã phát minh ra hình học tọa độ. Ông nghiên cứu hình học trên một mạng lưới tọa độ (có đánh số), sử dụng các nguyên lí đại số. Phát minh này mang đến cơ sở hình học tiên tiến hơn vì các nhà toán học có thể với các phương trình để tạo ra và thay đổi các đường thẳng, mặt phẳng, hoặc các hình dạng bên trong mạng lưới tọa độ.
Các nhà toán học người Pháp Pierre de Fermat và Blaise Pascal đã sáng tạo ra khái niệm xác suất toán học vào năm 1654. Xác suất liên quan đến việc đếm số những kết cục có thể có trong một tình huống để xác định khả năng của một kết cục nhất định là bao nhiêu. Khi bạn tung một đồng xu, nó có thể úp một trong hai mặt xuống. Vì thế xác suất nó nằm ngữa là một phần hai. Xác suất là một khái niệm quan trọng trong những lĩnh vực hiện đại thuộc thống kê, tài chính, khoa học và triết học.
Lĩnh vực giải tích, nghiên cứu sự biến đổi, xuất hiện một thập niên sau đó. Trong số nhiều công dụng của nó, giải tích được dùng để xác định đường cong, diện tích và thể tích. Vào năm 1665, Isaac Newton, một nhà khoa học và nhà toán học người Anh, đã nêu rõ hai toán tử cơ bản trong giải tích liên hệ với nhau như thế nào. Nhà triết học và toán học người Đức Gottfried Leibniz cũng phát triển lĩnh vực này một cách độc lập với Newton. Vào thập niên 1670, ông đã sáng tạo ra kí hiệu mà đa số học sinh học giải tích vẫn dùng để viết các phương trình. Giải tích đã đặt nền tảng cho vô số những tiến bộ trong kĩ thuật và cơ học, vật lí học, thống kê học, thiên văn học, kinh tế học, y học, và nhiều lĩnh vực khác.
TỪ TOÁN HỌC ĐẾN MÁY VI TÍNH
Các nhà toán học tiếp tục kế thừa nhau xây dựng và cải tiến các ý tưởng. Nhưng chúng ta tiến từ giải tích đến laptop như thế nào?
Bàn tính và Máy cơ Antikythera là những phiên bản sơ khai của máy tính hoặc máy vi tính. Thước trượt, một công cụ trượt có đánh số được phát minh vào thế kỉ thứ 17, cũng thế. Thước trượt tiết kiệm thời gian và sai số trong tính toán. Người dùng có thể trả lời một phép tính bằng cách gắn cho khớp các phần của thước trượt với những con số nhất định.
Máy tính kĩ thuật số - như máy vi tính hiện đại – là những cỗ máy có khả năng lập trình trước. Người dùng có thể lập trình chúng để thực hiện những công việc nhất định. Những cỗ máy đầu tiên như thế xuất hiện vào đầu thế kỉ thứ 19. Những cỗ máy được lập trình đầu tiên bao gồm một khung dệt và một máy vi tính cơ.
Nhà toán học người Anh Alan Turing nghiên cứu sự điện toán vào thập niên 1930. Các ý tưởng của ông đã mang đến cho ông danh hiệu cha để của ngành khoa học máy tính. Tuy nhiên, người Mĩ George Stibitz thường được xem là cha đẻ của máy vi tính hiện đại. Vào năm 1937, ông đã chế tạo ra chiếc máy tính đầu tiên sử dụng hệ đếm nhị phân, hay mã nhị phân, để thực hiện tính toán số học. Mã nhị phân sử dụng sự kết hợp của 0 và 1. Thí dụ, số 9 trong hệ thập phân có thể viết là 1001 trong hệ nhị phân. Tất cả máy vi tính hiện đại đều sử dụng mã nhị phân khi thực hiện các phép tính bên trong chúng.
Khi máy vi tính điện tử, kĩ thuật số phát triển trong thế kỉ 20, chúng phát triển cả về khả năng và kích cỡ. Các nhà khoa học đã phát triển phần cứng để lưu trữ thông tin. Điều này đã biến máy tính thành máy lưu trữ dữ liệu như chúng ta biết. Những chiếc máy vi tính kích cỡ bằng căn phòng đã được chế tạo trong thập niên 1950 và 1960 để xử lí những phép tính ngày một tiến bộ hơn. Sau đó, vào thập niên 1970, sự phát minh ra bộ vi xử lí đã giúp máy vi tính thu nhỏ kích cỡ hết sức ngoạn mục. Vào thập niên 1980, một chiếc máy tính cá nhân đã có thể đặt vừa trên bàn làm việc.
Nhờ khả năng xử lí vô song của máy vi tính, người hiện đại có thể làm việc nhanh hơn và ít sai sót hơn so với tổ tiên của chúng ta. Máy vi tính giải quyết nhanh gọn những phép tính mà người ta mất cả đời người để thực hiện. Vì lí do này mà chúng đã cho phép vô số phát triển trong ngành toán học, khoa học, và những lĩnh vực khác. Nhưng không thành tựu nào trong số này có thể thành hiện thực nếu như không có công nghệ tính toán của người cổ đại. Các hệ thống đo, đếm, và tính toán của họ đã mang lại cho chúng ta những công cụ mà chúng ta hàng ngày.
Công nghệ tính toán thời cổ đại
Michael Woods & Mary B. Woods
Trần Nghiêm dịch
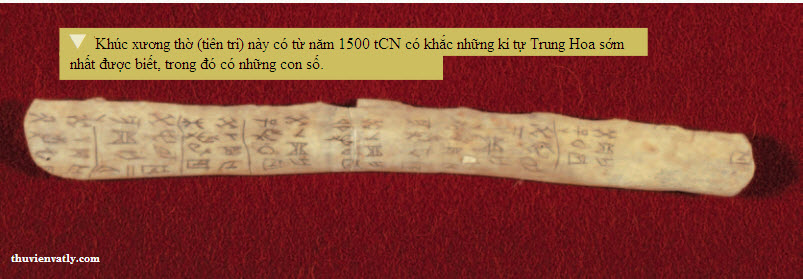
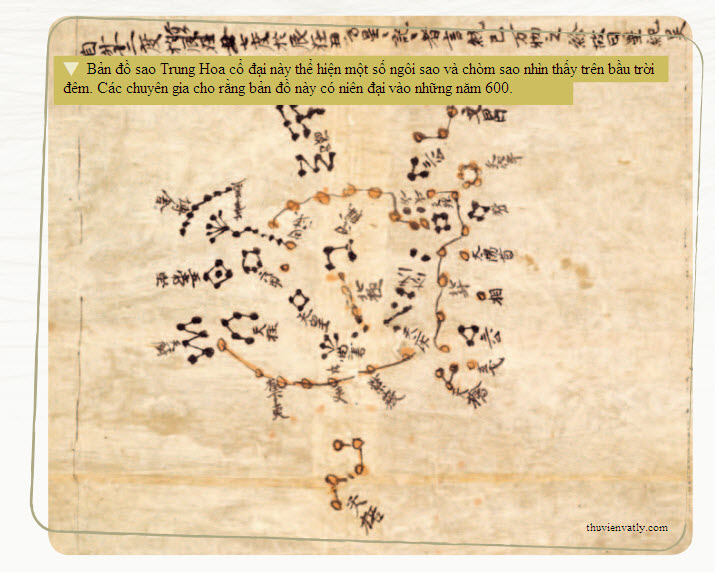
![[Sách] Công nghệ tính toán thời cổ đại](/bai-viet/images/stories/hiepkhachquay3/cntt1.bmp)
