Chúng tôi trích giới thiệu với các bạn một số bản dịch từ tác phẩm Những câu hỏi và bài tập vật lí phổ thông của hai tác giả người Nga L. Tarasov và A. Tarasova, sách xuất bản ở Nga năm 1968. Bản dịch lại từ bản tiếng Anh xuất bản năm 1973.
Các bài giảng được trình bày dưới dạng thảo luận hỏi đáp giữa giáo viên (GV) và học sinh (HS).
§25. Bài toán chuyển động trong điện trường đều
GV: Giả sử một vật tích điện chuyển động trong một điện trường đều, tức là trong một điện trường mà mỗi điểm có cường độ điện trường bằng nhau về độ lớn E và cùng chiều. Một ví dụ là điện trường nằm giữa hai bản tụ của một tụ phẳng. Các em có thấy sự tương đồng nào giữa bài toán chuyển động của một vật tích điện trong điện trường đều và bất kì bài toán nào đã biết trước đây không?
HS B: Theo em thấy nó có liên hệ gần gũi với bài toán chuyển động của một vật trong trường hấp dẫn. Trên những khoảng cách tương đối ngắn, trường hấp dẫn của Trái đất có thể xem là đều.
GV: Đúng rồi. Vậy đâu là sự khác biệt giữa chuyển động trong điện trường và trong trường hấp dẫn?
HS B: Lực tác dụng lên vật là khác nhau. Trong điện trường, lực tác dụng lên vật là Fe = Eq (nó truyền một gia tốc ae = Eq/m cho vật). Lực trong trường hấp dẫn là P = mg (truyền gia tốc g cho vật). Ở đây m là khối lượng của vật và q là điện tích của nó.
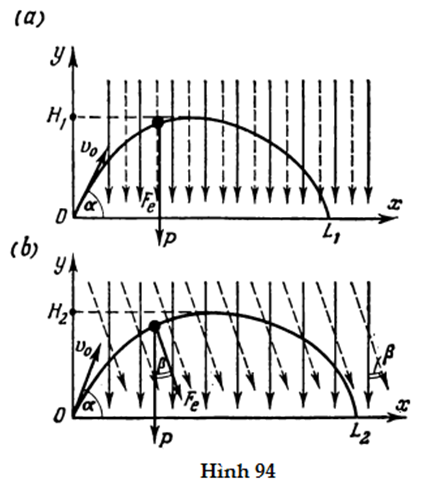
GV: Tôi ước gì thí sinh nào cũng có thể hiểu sự thật đơn giản là chuyển động của một vật trong một trường đều bất kì về mặt động học là như nhau. Cái khác nhau chỉ là giá trị của lực tác dụng lên vật trong những trường khác nhau. Chuyển động của một vật tích điện trong một điện trường đều có cùng bản chất với chuyển động của một hòn đá bình thường trong trọng trường của Trái đất. Ta hãy xét một bài toán trong đó chuyển động của một vật xảy ra đồng thời trong hai trường: trọng trường và điện trường. Một vật khối lượng m, điện tích +q được ném lên xiên một góc α so với phương ngang, với vận tốc ban đầu v0. Vật chuyển động đồng thời trong trọng trường và điện trường đều có cường độ E. Đường sức của hai trường đều hướng thẳng đứng xuống dưới (Hình 94a). Tìm thời gian chuyển động T1, tầm xa L1 và độ cao cực đại H1.
HS B: Có hai lực tác dụng lên vật: trọng lực P = mg và lực điện Fe = Eq. Trong trường hợp đã cho, hai lực đó song song nhau. Và như trong §5, em có thể phân tích vector vận tốc ban đầu thành các thành phần hướng theo hai chiều...
GV (cắt ngang): Dừng lại chút! Các em có muốn làm lại phần chứng minh ở bài toán tương tự ở §5 không?
HS B: Có chứ, nhưng nên ngắn gọn thôi.
GV: Không cần làm thế. Các em có thể sử dụng trực tiếp kết quả ở các phương trình (15), (16) và (17). Chỉ cần tưởng tượng rằng vật đang chuyển động trong một trường hấp dẫn “mạnh hơn” được đặc trưng bởi một gia tốc toàn phần bằng g + Eq/m. Trong các phương trình (15), (16) và (17) ta thay

HS A: Ở đây có một chỗ em không hiểu. So với bài toán tương ứng ở §5, có thêm một lực Fe tác dụng trong bài toán đã cho. Lực này hướng thẳng đứng xuống dưới và do đó không ảnh hưởng đến chuyển động ngang của vật. Vậy tại sao, trong trường hợp đã cho, nó lại ảnh hưởng đến tầm bay xa L1?
GV: Tầm bay xa phụ thuộc vào thời gian bay, và thời gian này được xác định bằng cách xét chuyển động theo phương thẳng đứng của vật.
Bây giờ chúng ta sẽ thay đổi một chút các điều kiện của bài toán: giả sử các đường sức điện trường hợp một góc β với phương thẳng đứng (Hình 94b). Giống như bài trước, hãy tìm thời gian chuyển động T2, tầm bay xa L2 và độ cao cực đại H2.
HS A: Trước tiên, em sẽ phân tích lực Fe thành hai thành phần: thẳng đứng (Fe cosβ) và nằm ngang (Fe sinβ). Bài toán này khiến em nhớ tới bài toán vết gió thổi ở §5. Ở đây thành phần Fe sinβ đóng vai trò “lực của gió”.
GV: Khá hợp lí. Chỉ cần nhớ rằng, trái với bài toán vết gió mà em nói, ở đây chúng ta có một lực thẳng đứng khác, đó là: mg + Fe cosβ.
HS A: Em sẽ sử dụng phương trình (15), (16) và (18), trong đó em sẽ thay như sau

GV: Hoàn toàn chính xác. Thật đáng tiếc là các thí sinh thường không thấy được sự tương tự giữa chuyển động trong trường hấp dẫn và chuyển động trong điện trường đều. Vì thế, các bài toán như vậy thường hết sức khó khăn đối với các em.
HS A: Chúng em đã không học những bài toán như thế trước đây. Bài toán duy nhất thuộc loại này mà em từng gặp là về chuyển động của một electron giữa hai bản tụ song song, nhưng chúng ta bỏ qua tác dụng của trường hấp dẫn lên electron. Theo em nhớ thì những bài toán như vậy thường hết sức khó.
GV: Toàn bộ những bài toán này là trường hợp đặc biệt của bài toán minh họa ở Hình 94a, vì trong chuyển động của một electron bên trong một tụ điện thì tác dụng của trọng trường là có thể bỏ qua. Chúng ta hãy xét một bài toán như thế.
Với vận tốc ban đầu v0, một electron bay vào trong một tụ phẳng hợp một góc α1 và rời khỏi tụ với góc α2 so với bản tụ như thể hiện trong Hình 95. Độ dài của bản tụ là L. Tìm cường độ E của điện trường trong lòng tụ và động năng của electron khi nó vừa ra khỏi tụ. Khối lượng m và điện tích q của electron là đã biết.

Tôi kí hiệu v2 là vận tốc của electron khi nó bay ra khỏi tụ. Theo phương song song với bản tụ, electron bay với vận tốc không đổi. Điều này cho phép chúng ta xác định thời gian bay bên trong tụ

Động năng của electron khi nó bay ra khỏi tụ điện là

Giải như vậy các em đã thấy rõ ràng chưa?
HS A: Vâng, giờ thì em biết cách giải những bài toán như thế rồi.
GV: Cũng đáng quan tâm là những bài toán về dao động của một con lắc với quả lắc tích điện đặt trong một tụ phẳng. Chúng ta sẽ xét bài toán sau đây. Một quả lắc khối lượng m tích điện tích q được treo lơ lửng bên dưới một sợi dây mảnh chiều dài l bên trong một tụ phẳng với hai bản tụ đặt nằm ngang. Cường độ điện trường E trong lòng tụ và các đường sức điện hướng thẳng đứng xuống dưới (Hình 96a). Tìm chu kì dao động của con lắc.

HS B: Vì trong trường hợp đã cho, các đường sức của trường tĩnh điện và trọng trường là cùng chiều, nên em có thể sử dụng kết quả của phương trình (75) cho một con lắc bình thường sau khi thay tổng các gia tốc (g + Eq/m) cho gia tốc trọng trường g. Như vậy, chu kì dao động cần tìm sẽ là
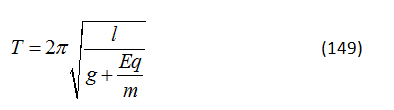
GV: Khá chính xác. Như các em thấy, bài toán đã cho rất đơn giản nếu các em có khả năng sử dụng sự tương tự giữa chuyển động trong điện trường đều và trong trọng trường.
HS A: Phương trình (149) giống phương trình (77) ở cấu trúc của nó.
GV: Điều này khá đúng. Chỉ có điều trong phương trình (77) số hạng thêm cho gia tốc g là do gia tốc của hệ quy chiếu (trong đó dao động của con lắc được nghiên cứu), còn trong phương trình (149) số hạng đó xuất hiện cùng với sự có mặt của một tương tác bổ sung.
Phương trình (149) sẽ thay đổi như thế nào nếu dấu của điện tích trên hai bản tụ bị đảo lại?
HS A: Trong trường hợp này, chu kì dao động sẽ là
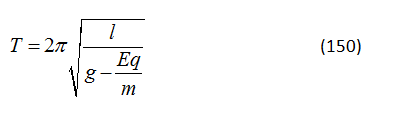
GV: Tốt. Điều gì sẽ xảy ra với con lắc nếu chúng ta tăng từ từ cường độ điện trường bên trong tụ?
HS A: Chu kì dao động sẽ tăng, tiến tới vô cùng khi E = mg/q. Nếu E tiếp tục tăng thêm thì chúng ta sẽ phải buộc sợi dây xuống bản dưới thay cho bản trên của tụ.
GV: Trong trường hợp này phương trình cho chu kì dao động sẽ có dạng ra sao?
HS A: Phương trình này sẽ có dạng

GV: Tốt lắm. Bây giờ chúng ta sẽ làm bài toán phức tạp thêm một chút. Chúng ta sẽ xét dao động của một con lắc với một quả lắc tích điện bên trong một tụ điện có hai bản tụ được định hướng không phải nằm ngang mà là thẳng đứng (Hình 96b). Trong trường hợp này, các gia tốc g và (Eq/m) vuông góc với nhau. Như bài trước, hãy tìm chu kì dao động của con lắc và, ngoài ra, tính góc α hợp bởi sợi dây với phương thẳng đứng khi con lắc ở vị trí cân bằng.
HS B: Theo hướng lập luận ở phần này và ở §12, em có thể kết luận ngay rằng: (1) chu kì dao động được biểu diễn theo gia tốc hiệu dụng g’, đó là tổng vector của gia tốc trọng trường và gia tốc của điện trường; và (2) hướng cân bằng của sợi dây trùng với vector gia tốc hiệu dụng vừa nói (hướng này được thể hiện trong Hình 96b bởi đường đứt nét). Như vậy

GV: Hoàn toàn chính xác. Tôi nghĩ bây giờ thì các em đã có thể dễ dàng khảo sát trường hợp tổng quát trong đó hai bản tụ hợp một góc β với phương ngang (Hình 96c). Vẫn là bài toán cũ: tìm chu kì dao động của con lắc và góc α hợp bởi hướng cân bằng của sợi dây con lắc và phương thẳng đứng.
HS A: Như trong trường hợp trước, gia tốc hiệu dụng bằng tổng vector của gia tốc trọng trường và gia tốc do điện trường. Chiều của gia tốc hiệu dụng này là chiều cân bằng của sợi dây con lắc. Có thể tìm gia tốc hiệu dụng g’ bằng định lí cosin lượng giác. Như vậy
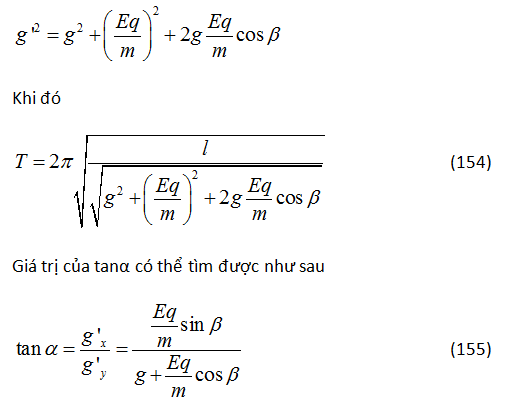
GV: Đáp số của em đúng rồi. Rõ ràng, với β = 0, chúng sẽ dẫn tới các kết quả cho trường hợp hai bản tụ nằm ngang, và với β = 90o thì dẫn tới các kết quả cho trường hợp hai bản tụ thẳng đứng. Các em hãy kiểm tra lại xem có phải vậy không.
HS B: Nếu β = 0, thì cos β = 1 và sin β = 0. Trong trường hợp này, phương trình (154) đơn giản thành phương trình (149) và tanα = 0 (vị trí cân bằng của sợi dây là thẳng đứng). Nếu β = 90o, thì cos β = 0 và sin β = 1. Trong trường hợp này, phương trình (154) trở thành phương trình (152), và phương trình (155) đơn giản thành phương trình (153).
GV: Tôi nghĩ chúng ta đã làm sáng tỏ hoàn toàn bài toán dao động của con lắc với quả lắc tích điện bên trong một tụ phẳng.
Để kết luận, tôi muốn các em tìm chu kì dao động của một con lắc có quả lắc tích điện, biết rằng tại điểm treo sợi dây con lắc có một điện tích khác cùng độ lớn và cùng dấu (Hình 97). Không có tụ điện nào cả.
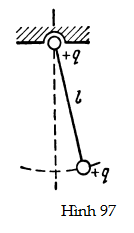
HS A: Theo định luật Coulomb, quả lắc sẽ chịu một lực đẩy từ phía điểm treo sợi dây bằng q2/l2. Lực này sẽ truyền một gia tốc q2/(l2m) cho quả lắc. Gia tốc này phải được tính đến trong phương trình cho chu kì dao động. Do đó, ta thu được biểu thức như sau

GV (nói với HS B): Em có đồng ý với kết quả này không?
HS B: Không, em không tán thành. Để cho phương trình (156) hợp lí, thì gia tốc q2/(l2m) phải hướng thẳng đứng xuống dưới trong suốt thời gian dao động. Thật ra thì gia tốc đó chỉ hướng như thế khi con lắc đi qua vị trí cân bằng. Như vậy, rõ ràng phương trình (156) là không đúng cho trường hợp bất kì. Tuy nhiên, em không nghĩ là mình tìm được đáp số chính xác.
GV: Em hiểu được cái sai trong phương trình (156) là hay lắm rồi. Trong trường hợp đã cho, lực điện tại mọi thời điểm hướng theo phương của sợi dây và do đó luôn luôn bị triệt tiêu bởi phản lực của sợi dây. Do đó, lực điện không góp phần cho lực hồi phục và như vậy nó không thể ảnh hưởng đến chu kì dao động của con lắc.
HS B: Như vậy có phải trong trường hợp đã cho thì chu kì dao động của con lắc sẽ được tính bằng phương trình (75) cho một con lắc với quả lắc không tích điện?
GV: Đúng rồi. Trong trường hợp chúng ta đang xét, trường lực điện không phải là đều và không thể liên hệ tương tự với trọng trường được.
Bài tập
45. Một electron bay vào một tụ phẳng theo chiều song song với hai bản tụ và cách bản tích điện dương dài 15 cm một khoảng 4 cm. Hỏi sau bao lâu thì electron sẽ rơi lên bản tụ này nếu cường độ điện trường bằng 500 V/m? Electron có thể có vận tốc tối thiểu bao nhiêu để nó bay vào trong tụ mà không rơi lên bản tụ? Khối lượng của electron là 9.10-28 g và điện tích electrong là 4,8.10-10 esu (đơn vị tĩnh điện).
46. Một electron bay vào một tụ phẳng theo phương song song với hai bản của nó với vận tốc ban đầu 3.106 m/s. Tìm cường độ điện trường trong lòng tụ nếu electron bay ra hợp một góc 30o với bản tụ. Bản tụ dài 20 cm. Khối lượng và điện tích electron là đã biết (xem bài 45).
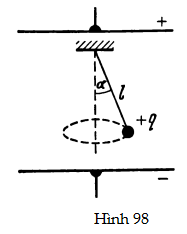
47. Bên trong một tụ phẳng có cường độ điện trường E, một quả lắc khối lượng m và điện tích +q được treo lơ lửng bên dưới một sợi dây chiều dài l, chuyển động quay đều theo một vòng tròn (Hình 98). Góc nghiêng của sợi dây là α. Tìm lực căng dây và động năng của quả lắc.
48. Hai quả cầu khối lượng m1 và m2 với điện tích +q1 và +q2 được nối với nhau bởi một sợi dây vắt qua một cái ròng rọc. Tính gia tốc của hai quả cầu và lực căng dây nếu toàn bộ hệ được đặt trong một điện trường đều E có các đường sức điện hướng thẳng đứng xuống dưới. Bỏ qua mọi tương tác giữa hai quả cầu tích điện.
49. Một quả cầu khối lượng m tích điện +q có thể quay trong một mặt phẳng thẳng đứng tại đầu của một sợi dây chiều dài l trong một điện trường đều có các đường sức điện hướng thẳng đứng lên trên. Phải truyền cho quả cầu một vận tốc ngang bằng bao nhiêu tại vị trí cao nhất của nó để cho lực căng của sợi dây tại vị trí thấp nhất của quả cầu bằng 10 lần trọng lượng của quả cầu?
Những câu hỏi và bài tập vật lí phổ thông
L. Tarasov và A. Tarasova
Trần Nghiêm dịch
Phần tiếp theo >>