Chúng tôi trích giới thiệu với các bạn một số bản dịch từ tác phẩm Những câu hỏi và bài tập vật lí phổ thông của hai tác giả người Nga L. Tarasov và A. Tarasova, sách xuất bản ở Nga năm 1968. Bản dịch lại từ bản tiếng Anh xuất bản năm 1973.
Các bài giảng được trình bày dưới dạng thảo luận hỏi đáp giữa giáo viên và học sinh.
§12. Con lắc ở trạng thái không trọng lượng
GV: Giả sử chúng ta đóng một cái đinh vào thành thang máy và treo một quả lắc dưới một sợi dây chiều dài l buộc vào cái đinh đó. Sau đó chúng ta kích thích quả lắc để nó thực hiện dao động điều hòa. Giả sử thang máy đang đi lên với gia tốc a. Hỏi chu kì dao động của con lắc là bao nhiêu?
HS A: Khi chúng ta đang đi lên bên trong một máy đang chuyển động có gia tốc, ta cảm nhận một sự tăng nhất định của trọng lượng. Rõ ràng con lắc cũng “cảm thấy” sự tăng giống như vậy. Em nghĩ chu kì dao động của nó có thể tính bằng công thức
Tuy nhiên, em không thể chứng minh công thức này một cách chặt chẽ.
GV: Công thức của em là đúng. Nhưng để chứng minh nó, ta cần chấp nhận một quan niệm mới đối với chúng ta. Từ trước đến giờ chúng ta chỉ xét những vật nằm trong những hệ quy chiếu quán tính, tránh né những hệ quy chiếu phi quán tính. Hơn nữa, tôi còn khuyên các em không nên sử dụng những hệ quy chiếu phi quán tính (xem §4). Nhưng trong trường hợp hiện tại, sẽ thuận tiện hơn nếu chúng ta sử dụng hệ quy chiếu gắn liền với cái thang máy đang gia tốc này. Nhắc lại rằng khi xét chuyển động của một vật khối lượng m trong một hệ quy chiếu phi quán tính có gia tốc a, ta phải đưa thêm một lực nữa tác dụng vào vật. Lực này gọi là lực quán tính, bằng ma và tác dụng ngược chiều với gia tốc. Sau khi có lực quán tính tác dụng lên vật, ta có thể quên đi chuyện hệ quy chiếu đang chuyển động có gia tốc, và xét chuyển động như thể nó xảy ra trong một hệ quy chiếu quán tính. Trong trường hợp cái thang máy, ta phải tác dụng thêm một lực ma lên quả lắc. Lực này không đổi về độ lớn và chiều của nó biến đổi và trùng với chiều của trọng lực mg. Như vậy, từ phương trình (75) gia tốc g sẽ được thay bằng tổng số học của các gia tốc (g + a). Từ đó ta thu được công thức (77) mà em vừa nêu.
HS A: Như vậy, nếu thang máy đang đi xuống với gia tốc a hướng xuống, thì chu kì dao động sẽ được xác định bởi hiệu gia tốc (g – a), vì ở đây lực quán tính ma ngược chiều với trọng lực. Như vậy có đúng không thầy?
GV: Tất nhiên rồi. Trong trường hợp này chu kì dao động của con lắc là
Công thức có nghĩa với điều kiện a < g. Giá trị của gia tốc a càng gần với g thì chu kì của con lắc càng lớn. Khi a = g thì trạng thái không trọng lượng xảy ra. Chuyện gì sẽ xảy ra với con lắc trong trường hợp này?
HS A: Theo công thức (78), chu kì trở nên lớn vô hạn. Điều này phải có nghĩa là con lắc đứng yên.
GV: Chúng ta hãy làm rõ một số chi tiết trong câu trả lời của em. Chúng ta bắt đầu với con lắc đang dao động trong thang máy. Hết sức bất ngờ, thang máy đứt dây và rơi tự do xuống theo phương thẳng đứng (bỏ qua sức cản của không khí). Cái gì xảy ra với con lắc đây?
HS A: Như em đã nói, con lắc ngừng lắc.
GV: Câu trả lời của em không đúng lắm. Con lắc sẽ thật sự đứng yên (tất nhiên, đối với cái thang máy) nếu tại thời điểm con lắc đứt dây quả lắc đang ở vị trí biên của nó. Nếu tại thời điểm đó con lắc không ở vị trí biên thì nó sẽ tiếp tục quay của cuối sợi dây trong một mặt phẳng thẳng đứng với một tốc độ không đổi bằng tốc độ của nó tại thời điểm tai nạn xảy ra.
HS A: Giờ thì em đã hiểu.
GV: Bây giờ hãy hình dung hành trạng của một con lắc (quả lắc gắn với sợi dây) bên trong một phi thuyền vũ trụ ở trạng thái không trọng lượng.
HS A: Trong phi thuyền vũ trụ, quả lắc ở cuối sợi dây hoặc sẽ là đứng yên (so với phi thuyền), hoặc sẽ quay trong một vòng tròn có bán kính được xác định bởi chiều dài của sợi dây (tất nhiên nếu không đụng trúng thành hoặc trần phi thuyền).
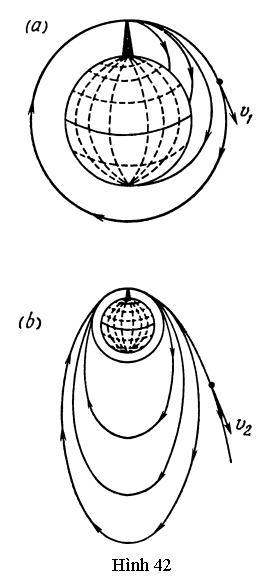
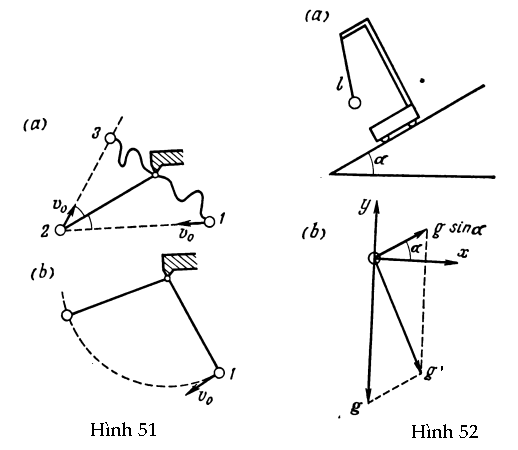
GV: Bức tranh của em không hoàn chỉnh cho lắm. Giả sử chúng ta đang ở trong một phi thuyền ở trạng thái không trọng lượng. Chúng ta lấy quả lắc và sợi dây và buộc đầu tự do của sợi dây sao cho thành hoặc trần phi thuyền không gây cản trở cho chuyển động của con lắc. Sau đó chúng ta thận trọng thả quả lắc ra. Quả lắc vẫn đứng yên. Ở đây chúng ta phân biệt hai trường hợp: (1) sợi dây chùng, và (2) sợi dây căng. Xét trường hợp thứ nhất (vị trí 1 ở Hình 51a). Chúng ta truyền một vận tốc nhất định v0 cho quả lắc. Khi đó quả lắc sẽ chuyển động thẳng với vận tốc không đổi cho đến khi sợi dây hết chùng (vị trí 2 ở Hình 51a). Tại thời điểm này, phản lực của sợi dây sẽ tác dụng lên quả lắc theo kiểu giống như phản lực của tường tác dụng lên quả bóng bật vào nó. Như thế, hướng chuyển động của quả lắc sẽ thay đổi đột ngột và nó sẽ lại chuyển động với vận tốc không đổi theo đường thẳng (vị trí 3 ở Hình 51a). Ở dạng phản xạ kì cục này, quy luật bằng nhau của góc tới và góc phản xạ sẽ được nghiệm đúng. Bây giờ xét trường hợp thứ hai: trước tiên chúng ta kéo cho sợi dây căng, sau đó nhẹ nhàng thả quả lắc ra. Như trong trường hợp thứ nhất, quả lắc sẽ đứng yên tại vị trí nó được thả ra (vị trí 1, Hình 51b). Sau đó chúng ta truyền một vận tốc nhất định v0 cho quả lắc theo hướng vuông góc với sợi dây. Khi đó con lắc bắt đầu quay trong một vòng tròn với vận tốc không đổi. Mặt phẳng quay được xác định bởi sợi dây và vector vận tốc đã truyền cho quả lắc.
Bây giờ chúng ta hãy xét bài toán sau. Một sợi dây chiều dài l có một quả lắc tại đầu dưới được buộc vào một xe tải trượt không ma sát xuống một mặt phẳng nghiêng có góc nghiêng α (Hình 52a). Chúng ta hãy tìm chu kì dao động của con lắc này trong một hệ quy chiếu chuyển động với một gia tốc nhất định. Tuy nhiên, trái với bài toán cái thang máy ở phần trước, gia tốc của hệ hợp một góc với gia tốc trọng trường. Như vậy phát sinh thêm một câu hỏi nữa: hướng cân bằng của sợi dây con lắc là hướng nào?
HS A: Em đã từng thử phân tích một bài toán như vậy nhưng rồi đành bó tay, không giải nổi.
GV: Chu kì dao động của con lắc trong trường hợp này được tính bằng công thức (75) ngoại trừ là g được thay bằng một gia tốc hiệu dụng nhất định như trong trường hợp cái thang máy. Gia tốc này (ta sẽ kí hiệu là g’) bằng tổng vector của gia tốc trọng trường và gia tốc của hệ đã cho. Một vấn đề nữa cần xét tới trong tổng vector vừa nói, vector gia tốc của xe tải sẽ có dấu ngược lại, vì lực quán tính ngược chiều với gia tốc của hệ. Các vector gia tốc được vẽ trên Hình 52b, gia tốc của xe tải bằng g sinα. Tiếp theo ta tìm g’.
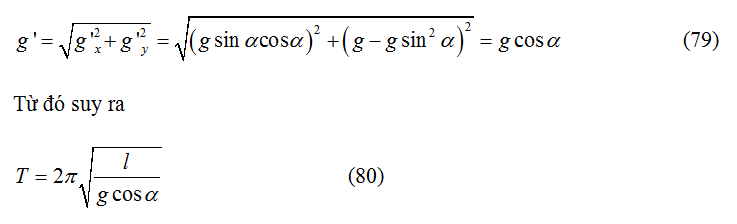
HS A: Làm thế nào chúng ta có thể xác định hướng cân bằng của sợi dây?
GV: Đó chính là hướng của gia tốc g’. Trên cơ sở phương trình (79), dễ dàng thấy rằng hướng này hợp một góc α với phương thẳng đứng. Nói cách khác, ở vị trí cân bằng, sợi dây của một con lắc treo trên một xe tải đang trượt xuống một mặt phẳng nghiêng sẽ vuông góc với mặt phẳng đó.
HS B: Có cách nào khác thu được kết quả vừa có hay không thầy?
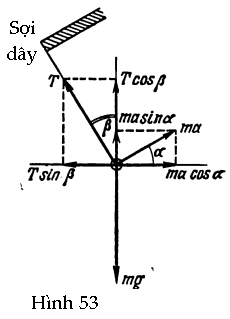
GV: Chúng ta có thể đi tới kết luận giống như vậy trực tiếp bằng cách xét sự cân bằng của quả lắc so với xe tải. Các lực tác dụng lên quả lắc là: trọng lực mg, lực căng T của sợi dây và lực quán tính ma (Hình 53). Ta kí hiệu góc hợp bởi sợi dây và phương thẳng đứng là β.
Tiếp theo ta phân tích toàn bộ những lực này theo phương thẳng đứng và phương ngang, sau đó viết điều kiện cân bằng cho các thành phần lực thuộc mỗi phương này. Ta có
Sau khi chia phương trình này cho phương trình kia ta được
cot β = cot α
Như vậy góc β và α hóa ra bằng nhau. Vì thế, hướng cân bằng của con lắc là vuông góc với mặt phẳng nghiêng.
HS B: Em đã theo dõi những lí giải của thầy rất kĩ và đi tới kết luận rằng xét cho cùng thì em chẳng có sai khi trả lời câu hỏi của thầy về lực tác dụng lên một vệ tinh, em đã chỉ ra trọng lực và lực li tâm (xem §8). Nói đơn giản thì câu trả lời của em đi liền với hệ quy chiếu gắn với vệ tinh, và lực li tâm được hiểu là lực quán tính. Trong hệ quy chiếu phi quán tính gắn với vệ tinh, chúng ta có một bài toán, không phải động lực học, mà là tĩnh học. Đó là bài toán cân bằng của các lực trong đó một lực là lực quán tính li tâm.
GV: Một cách tiếp cận với bài toán vệ tinh như thế là được phép. Tuy nhiên, khi nói tới lực li tâm ở §8, em đã không xem nó là một lực quán tính. Lúc ấy em chỉ đang cố nghĩ ra cái gì đó giữ vệ tinh lại để nó đừng rơi xuống đất. Hơn nữa, trong trường hợp em đề cập, không cần thiết phải chọn hệ quy chiếu gắn với vệ tinh: bản chất vật lí của bài toán được chứng minh rõ ràng hơn mà không cần sử dụng lực quán tính li tâm. Lời khuyên của tôi trước đây vẫn có giá trị: nếu không có yêu cầu đặc biệt, đừng nên sử dụng hệ quy chiếu phi quán tính.
Những câu hỏi và bài tập vật lí phổ thông
L. Tarasov và A. Tarasova
Trần Nghiêm dịch
Phần tiếp theo >>
