Mặt dốc đẳng thời
1673
Christiaan Huygens (1629-1695)
Nhiều năm trước, tôi có viết một câu chuyện về bảy nhà trượt tuyết tìm thấy một cung đường núi có vẻ thần kì. Cho dù họ bắt đầu trượt xuống từ vị trí nào trên cung đường đó thì họ luôn đi tới đáy dốc với thời gian y hệt nhau. Làm sao có thể như vậy được? Vào thế kỉ mười bảy, các nhà toán học và nhà vật lí đã tìm kiếm một đường cong đặc trưng cho hình dạng của một kiểu mặt dốc hay cung đường đặc biệt. Trên mặt dốc đặc biệt này, các vật phải trượt xuống tận đáy dốc với lượng thời gian đúng bằng nhau, bất chấp vị trí xuất phát. Các vật được gia tốc bởi trọng lực, và mặt dốc được xem là không ma sát.
Nhà toán học, nhà thiên văn học, và nhà vật lí học Hà Lan Christiaan Huygens đã tìm ra một nghiệm vào năm 1673 và công bố nó trong quyển sách Horologium Oscillatorium (Đồng hồ Con lắc). Nói theo chuyên môn, đường đẳng thời (tautochrone) là một cycloid – nghĩa là, một đường cong được vạch ra bởi một điểm trên rìa của một vòng tròn khi vòng tròn đó lăn theo một đường thẳng. Đường đẳng thời còn được gọi là đường đoản thời (brachistochrone) khi muốn nói tới đường cong đem lại tốc độ trượt xuống nhanh nhất cho một vật không ma sát khi vật trượt xuống từ điểm này đến điểm kia.
Huygens đã cố sử dụng khám phá của ông để thiết kế một đồng hồ con lắc chính xác hơn. Đồng hồ khai thác các cung cycloid nghịch gần chốt treo con lắc để đảm bảo dây treo đi theo đường cong tối ưu, cho dù con lắc bắt đầu đong đưa từ vị trí nào. (Lạy thánh Alas, lực ma sát do sự uốn cong của dây treo dọc theo các cung đó gây ra sai số còn lớn hơn cái nó hiệu chỉnh được.)
Tính chất đặc biệt của đường đẳng thời được nhắc tới trong tiểu thuyết Cá Voi Trắng trong một đoạn nói về nồi thử, một cái nồi dùng để chưng cất mỡ cá lấy dầu: “[Nồi thử] còn là chốn thiền định toán học sâu sắc. Chính trong cái nồi thử tay trái của Pequod, với cục đá xà phòng xoay quanh tôi một cách cần mẫn, lần đầu tiên tôi gián tiếp bắt gặp một thực tế đáng chú ý, rằng trong hình học mọi vật thể trượt theo một đường cycloid, như cục đá xà phòng của tôi chẳng hạn, nó sẽ trượt xuống từ bất kì điểm nào với thời gian đúng bằng nhau.”

Christiaan Huygens, tranh vẽ của Caspar Netscher (1639-1684).
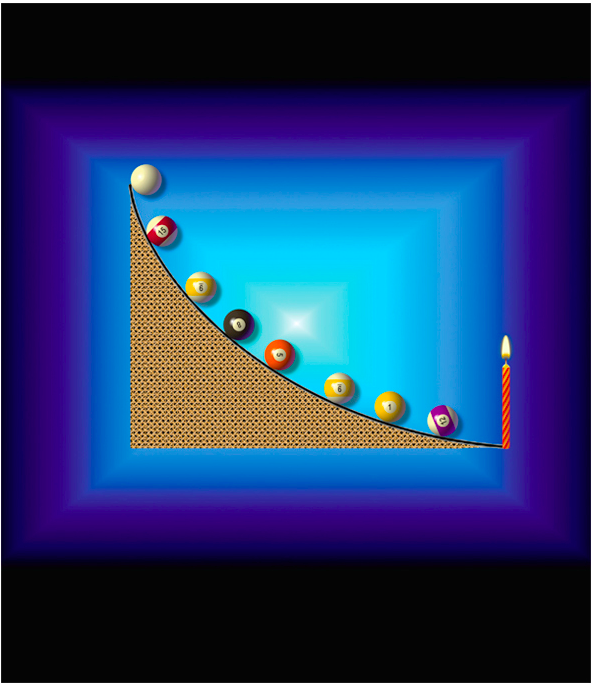
Dưới tác dụng của trọng lực, các quả billard này lăn theo mặt dốc đẳng thời từ những vị trí xuất phát khác nhau, nhưng chúng sẽ đi tới chỗ ngọn nến với thời gian bằng nhau. Các quả billard được đặt lên mặt dốc, tuần tự mỗi lần một quả.
XEM THÊM. Gia tốc của vật rơi (1638), Vòng Clothoid (1901).
250 Mốc Son Chói Lọi Trong Lịch Sử Vật Lí
Clifford A. Pickover
Bản dịch của Thuvienvatly.com
<< Phần trước | Phần tiếp theo >>