127. Vector là gì?
Một đoạn thẳng bất kì được gán chiều được gọi là một vector.
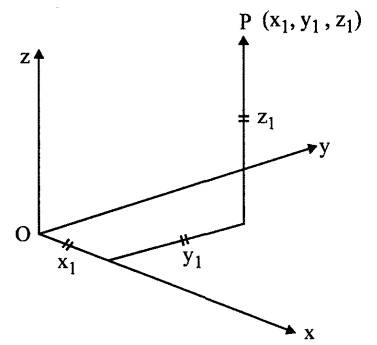
Như vậy, một đoạn thẳng từ O đến P là một vector, nó có độ dài là OP và có chiều từ O đến P.
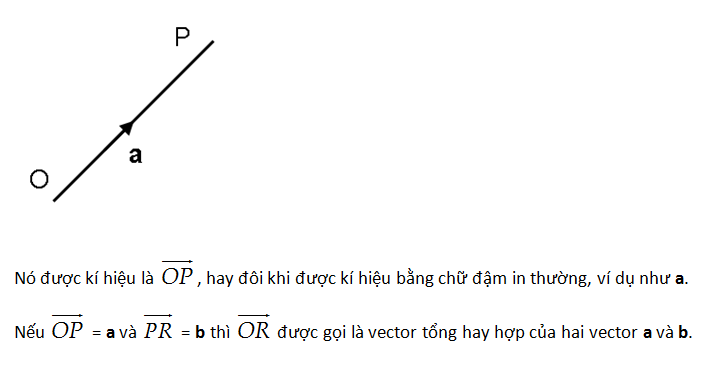

Lực và vận tốc là ví dụ của các đại lượng vector.
Tổng vector là một tổng hiểu theo nghĩa sau đây:

128. Trong trường hợp nào tích của hai vector là không giao hoán?
Với các vector, người ta định nghĩa hai loại tích.
Một được gọi là tích vô hướng, hay tích chấm. Nó có tính giao hoán nên với hai vector a và b bất kì, ta có a.b = b.a.
Loại thứ hai được gọi là tích vector, hay tích chéo. Nó không có tính giao hoán, vì với hai vector a và b bất kì, ta có (a × b) = - (b × a).
129. Ma trận là gì?
Một sắp xếp của các con số theo dạng hình chữ nhật được gọi là một ma trận.
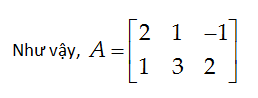
là một ma trận có 2 hàng và 3 cột, và được gọi là một ma trận cấp 2 × 3.
Một ma trận có m hàng và n cột được gọi là một ma trận m × n (đọc là ma trânh m nhân n).
130. Trong trường hợp nào tích của hai ma trận là không giao hoán?
Tích của hai ma trận thường là không giao hoán.

131. Lí thuyết ma trận được áp dụng ở đâu?
Ma trận có ích lợi lớn trong nhiều ngành toán học cao cấp, ví dụ như các phương trình đại số và phương trình vi phân, thiên văn học, cơ học, lí thuyết mạch điện, cơ học lượng tử, vật lí hạt nhân và khí động lực học.
132. Thế nào là một MIỀN NGUYÊN?
Một vành giao hoán được gọi là một miền nguyên, nếu
(i) Nó có phần tử đơn vị.
(ii) Nó không có ước số zero.
133. Ước số zero nghĩa là gì?
Nói ước số zero có nghĩa là các phần tử khác không a, b sao cho tích của chúng ab = 0.
Một ví dụ của những ước số như thế là trong cái gọi là modulo số học n.
Với một số nguyên n cho trước, người ta thu được các số như thế bằng cách chỉ sử dụng các số nguyên 0, 1, 2,..., n – 1.
Phép cộng và phép nhân được định nghĩa là số dư sau khi chia cho n của tổng và tích ban đầu của hai số nguyên bất kì của hệ.
Ví dụ, nếu n = 6 thì
2 + 4 ≡ 0, 2 + 5 ≡ 1, 3 + 5 ≡ 2, bởi vì
2 + 4 tức là 6, chia 6 cho số dư 0,
2 + 5 tức là 7, chia 6 cho số dư 1,
và 3 + 5 tức là 8, chia 6 cho số dư 2.
Tương tự, 2 × 3 ≡ 0, 4 × 5 ≡ 2.
2 và 3 được gọi là ước số zero của hệ gọi là “các số nguyên modulo 6”, bởi vì tích của chúng đồng dư với 0, nhưng 2 và 3 đều khác không.
Kí hiệu ≡ đọc là “đồng dư với”.
Nếu n là số nguyên tố thì không có ước số zero nào.
134. Trong một hệ thống toán học nhất định, 2 × 2 = 2 × 5. Hệ đó được gọi là gì?
Hệ đó được gọi là “các số nguyên modulo 6”, trong đó 4 đồng dư với 10, modulo 6,
Hay 4 ≡ 10 (mod 6).
Toán học – Những điều kì thú và những mốc son lịch sử
A.L. Audichya
Trần Nghiêm dịch
<< Phần trước | Phần tiếp theo >>