1. Chuyển động thẳng đều
6. Một hành khách ngồi trong một xe điện để ý thấy một đoàn tàu đi vào theo hướng ngược lại và gồm một đầu tàu và 10 toa mất 10 s để đi qua hết.
Hỏi tốc độ của tàu điện là bao nhiêu nếu chiều dài của mỗi toa tàu ở đoàn tàu bên kia là 16,5 m, chiều dài của đầu tàu cùng với toa than là 20 m và khoảng cách giữa các toa tàu là 1,5 m? Biết cả hai tàu đang chuyển động với cùng một tốc độ khi chúng gặp nhau.
7. Hỏi thời gian có bằng nhau để cho một chiếc thuyền đi hết 1 km xuôi dòng và ngược dòng trên một con sông (tốc độ của nước chảy là v1 = 2 km/h) và trên một cái hồ (nước phẳng lặng), nếu tốc độ của thuyền so với nước trong cả hai trường hợp là v2 = 8 km/h?
Giải bài toán này bằng tính toán và bằng đồ thị.
8. Xác định quãng đường mà thuyền đi được so với nước trên sông theo các điều kiện đã cho trong bài toán trên.
9. Mất một phút để một người khách đứng trên một cầu thang cuốn từ dưới đất lên tầng trên. Nếu thang cuốn không hoạt động thì anh ta mất ba phút để đi lên tầng trên.
Hỏi người khách đó sẽ mất bao lâu để đi tới tầng trên nếu anh ta đi trên cái thang cuốn đang chuyển động?
10. Một con thuyền mất 3 giờ để đi xuôi dòng từ điểm A tới điểm B và mất 6 giờ để đi ngược lại.
Con thuyền này sẽ mất bao lâu để thả xuôi dòng hết quãng đường AB nếu nó tắt máy?
11. Một máy bay đi từ điểm M đến điểm P và trở về với tốc độ v1 = 300 km/h (đối với không khí).
Hãy tính thời gian cần thiết cho toàn chuyến bay, biết gió thổi liên tục với vận tốc v2 = 60 km/h dọc theo đường bay. Khoảng cách giữa M và P là 900 km.
12. Hai chiếc thuyền đang đi xuôi dòng nước với vận tốc khác nhau. Khi một thuyền vượt qua thuyền kia thì một vòng phao được thả ra từ một trong hai thuyền. Sau đó chốc lát cả hai thuyền cùng quay đầu đồng thời và đi với tốc độ bằng như trước đó (so với nước) đến chỗ vòng phao được thả ra.
Hỏi thuyền nào sẽ đi tới chỗ vòng phao trước?
Đồng thời giải bài tập này cho các trường hợp trong đó hai thuyền: (1) đi ngược dòng; và (2) tiến về phía nhau trước khi chúng gặp nhau.
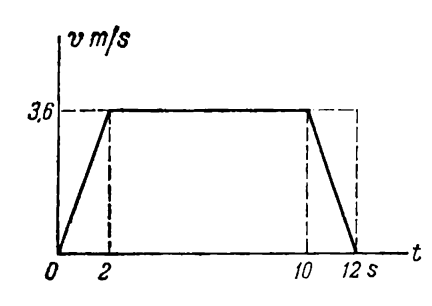
13. Một cái ống có thể xoay trong một mặt phẳng thẳng đứng được gắn trên một chiếc xe đẩy (Hình 1). Chiếc xe chuyển động đều trên mặt phẳng nằm ngang với tốc độ v1 = 2 m/s.
Cái ống được đặt hợp với phương ngang một góc α bằng bao nhiêu để các giọt nước mưa rơi thẳng đứng với vận tốc v2 = 6 m/s chuyển động song song với thành ống mà không chạm vào? Xem vận tốc của các giọt nước mưa là không đổi do sức cản không khí.
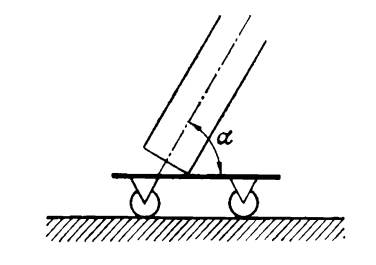
Hình 1
14. Một con tàu phá băng trượt theo một đường thẳng trên một mặt băng nhẵn với tốc độ v. Gió thổi với vận tốc u = 2v vuông góc với đường đi của con tàu.
Hỏi chong chóng gió gắn trên cột buồm của con tàu tự định hướng hợp một góc b bằng bao nhiêu với mặt buồm?
Buồm được căng ở góc 45o so với hướng gió.
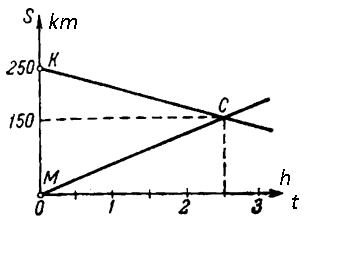
15. Một người ở trên thuyền băng qua sông từ điểm A (Hình 2). Nếu anh ta chèo thuyền vuông góc với bờ sông thì sau 10 phút anh ta sẽ đi tới điểm C nằm cách điểm B một đoạn S = 120 m về phía hạ lưu. Nếu người đó hướng thuyền ngược dòng hợp một góc α với đường thẳng AB (AB vuông góc với bờ sông) thì anh ta sẽ đi tới điểm B sau 12,5 phút.
Tính bề rộng l của con sông, vận tốc u của thuyền so với nước, tốc độ dòng chảy v và góc α. Giả sử vận tốc của thuyền so với nước là không đổi và có độ lớn bằng nhau trong hai trường hợp.
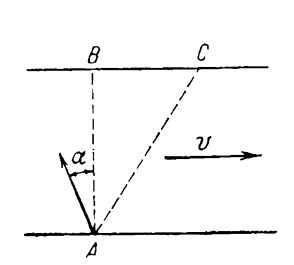
Hình 2
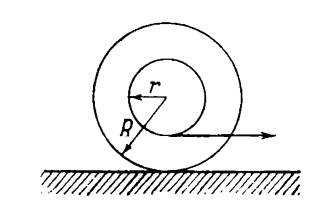
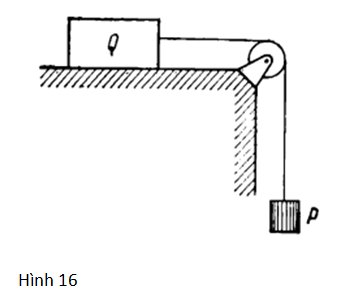
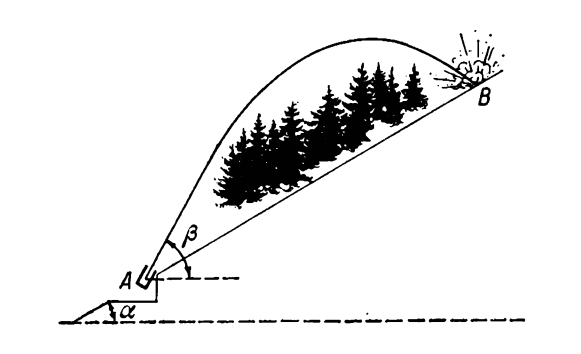
16. Một con thuyền chạy tuyến giữa hai điểm A và B nằm bên hai bờ sông (Hình 3), luôn luôn đi theo đường AB. Khoảng cách S giữa điểm A và điểm B là 1.200 m. Vận tốc của dòng nước v = 1,9 m/s là không đổi trên toàn bề rộng của con sông. Đường AB hợp một góc α = 60o với hướng dòng chảy.
Tính vận tốc u và góc β hợp với đường AB để thuyền đi hết quãng đường AB và trở về trong thời gian 5 phút. Góc β được giữ giống nhau trong hành trình đi từ A đến B và từ B về A.
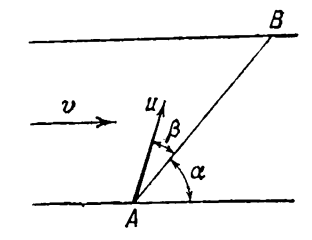
Hình 3
___________
ĐÁP SỐ VÀ GIẢI
6. v = 36 km/h.
Giải. Gọi v là tốc độ của tàu điện so với mặt đất thì vận tốc của nó so với đoàn tàu đang đi vào theo chiều ngược lại sẽ là 2v và có thể biểu diễn qua chiều dài l và thời gian đi qua t của đoàn tàu đang đi vào, tức là 2v = l/t, trong đó l = 16,5 × 10 + 10 × 1,5 + 20 = 200 m.
7. Thời gian đi trên sông gấp 1,07 lần thời gian đi trên hồ.
Giải. Thời gian chuyển động xuôi dòng là

Tỉ số của các thời gian chuyển động là
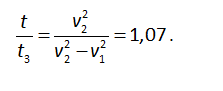

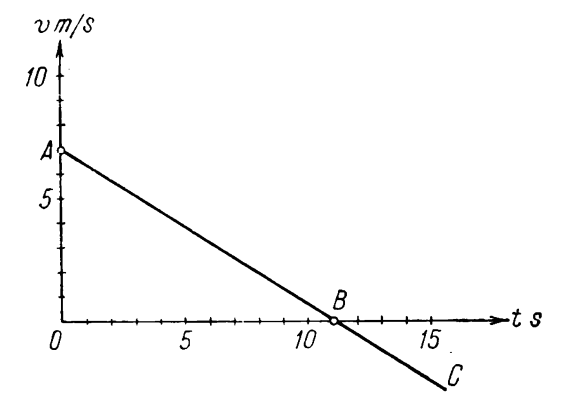
Hình 186
Hình 186 vẽ đồ thị của các chuyển động: I – chuyển động trên mặt nước phẳng lặng; II – chuyển động trên sông; t3 và t biểu diễn thời gian chuyển động cho hai trường hợp.
8. S1 = 2,1 km.
Giải. Khi đi xuôi dòng, thuyền sẽ đi được quãng đường, so với nước, là

9. t3 = 45 s.
Giải. Phương trình chuyển động cho ba trường hợp đã nêu trong bài toán là
S = v1t1, S = v2t2, S = (v1 + v2)t3
trong đó S là chiều dài của thang cuốn; v1 là vận tốc của nó; v2 là vận tốc của người khách trên thang cuốn đứng yên; t1 là thời gian đi lên của người khách đứng trên thang cuốn chuyển động; t2 là thời gian để anh ta đi lên khi thang cuốn đứng yên; t3 là thời gian cần thiết để đi lên khi người khách đi bộ trên thang cuốn đang chuyển động.
Giải các phương trình này ta được
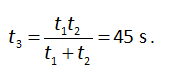
10. t3 = 12 h.
Giải. Phương trình chuyển động của thuyền đi từ A đến B và đi từ B về A là
S = (v1 + v2)t1 và S = (v1 – v2)t2
trong đó t1 = 3 h là thời gian đi xuôi dòng; t2 = 6 h là thời gian đi ngược dòng; v1 là vận tốc của thuyền so với nước; v2 là vận tốc của dòng nước; và S là khoảng cách giữa A và B.
Phương trình chuyển động của thuyền lúc tắt máy là S = v2t3.
Giải các phương trình này đồng thời cho t3 ta được
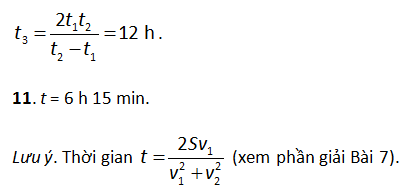
12. Trong cả ba trường hợp, hai thuyền sẽ đi tới vòng phao cùng một lúc.
Giải. Vận tốc của dòng chảy ảnh hưởng đến chuyển động của hai thuyền và vòng phao là giống nhau nên không làm thay đổi vị trí tương hỗ giữa chúng. Vì thế, vận tốc này có thể bỏ qua và chuyển động của hai thuyền và vòng phao chỉ được xét so với nước.
Quãng đường đi được bởi hai thuyền so với nước trong thời gian t trước khi chúng quay đầu sẽ là S1 = v1t và S2 = v2t.
Quay trở lại vòng phao với vận tốc v1 và v2 như ban đầu, rõ ràng hai thuyền sẽ mất thời gian bằng như cũ để đi hết quãng đường S1 và S2 đến chỗ vòng phao, giống như khi chúng chạy ra xa nó.
13. α = 71o35’.
Giải. Giọt mưa sẽ chuyển động tương đối so với ống theo phương thẳng đứng với vận tốc v2 và theo phương ngang với vận tốc v1 ngược chiều với chuyển động của xe đẩy. Vận tốc toàn phần v của giọt mưa so với ống sẽ bằng tổng hình học của hai vận tốc v1 và v2 (Hình 187).
Để cho các giọt mưa chuyển động song song với thành ống thì hướng của vector vận tốc v phải trùng với trục của ống. Như vậy,
tanα = v2/v1 = 3, α = 71o35’.
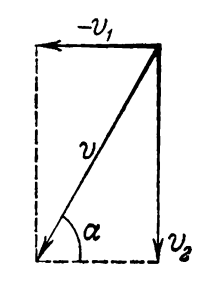
Hình 187
14. β = 18o30’.
Giải. Hướng của chong chóng gió sẽ trùng với hướng không khí chuyển động so với tàu phá băng. Vì con tàu chuyển động với tốc độ v, nên vận tốc toàn phần w của không khí so với tàu sẽ bằng tổng hình học của hai vận tốc v và u (Hình 188).
Vận tốc w sẽ hợp một góc α với hướng chuyển động của con tàu sao cho
tanα = u/v = 2
Góc giữa mặt phẳng cánh buồm và chong chóng gió sẽ là
β = α – 45o = 63o30’ – 45o = 18o30’.
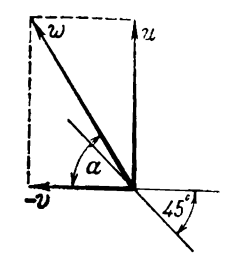
Hình 188
15. l = 200 m; u = 20 m/min; v = 12 m/min; α = 36o50’.
Giải. Trong cả hai trường hợp, chuyển động của thuyền bao gồm chuyển động tương đối của nó với nước và chuyển động của nó cùng với nước so với bờ sông.
Trường hợp thứ nhất (Hình 189). Thuyền đi dọc theo sông với vận tốc v và trong thời gian qua sông nó đi được quãng đường xuôi dòng là
l1 = vt1 (1)
Thuyền băng qua sông với vận tốc u và đi được quãng đường
l2 = ut1 (2)

Hình 189
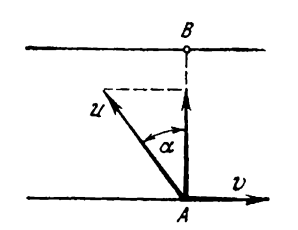
Hình 190
Trường hợp thứ hai (Hình 190). Vận tốc của thuyền dọc theo sông là bằng không, tức là
u sinα = v (3)
Vận tốc qua sông là u cosα, và quãng đường l2 đi được trong lúc qua sông sẽ là
l2 = u cosα t2 (4)
Giải hệ gồm 4 phương trình (1), (2), (3) và (4) ta được
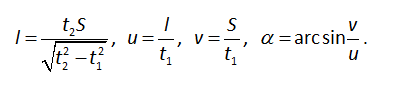
16. u = 8 m/s; β ≈12o.
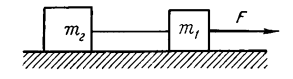
Giải. Như trong bài toán trước, vận tốc của dòng chảy và của thuyền sẽ được phân tích thành các thành phần hướng theo AB và vuông góc với nó (Hình 191). Để cho chuyển động của thuyền luôn hướng theo AB thì các thành phần vận tốc của dòng chảy và của thuyền theo phương vuông góc với AB phải bằng nhau, tức là
u sinβ = v sinα (1)

Hình 191

Hình 192
Khi thuyền đi từ A đến B, vận tốc của nó so với bờ sông sẽ là u cosβ + v cosα và thời gian chuyển động sẽ được xác định từ phương trình

Bài tập vật lí phổ thông
V. Zubov và V. Shalnov
Trần Nghiêm dịch (theo bản tiếng Anh in năm 1974)
<< Phần trước | Phần tiếp theo >>




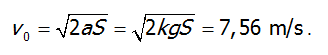
![[Ebook] Những câu hỏi và bài tập vật lí phổ thông](/bai-viet/images/2013/07/cauhoivabaitap.png)