42. Định lí Wilson là gì?
Định lí Wilson phát biểu rằng:
Số (n – 1)! + 1 là chia hết cho n, nếu và chỉ nếu n là số nguyên tố.
Ví dụ, với n = 5, (n – 1)! + 1 bằng 25 chia hết cho 5, vì 5 là số nguyên tố.
Nhưng nếu n = 6, thì (n – 1)! + 1 bằng 121 không chia hết cho 6, vì 6 không phải là số nguyên tố.
43. Người ta sử dụng phép quy nạp toán học như thế nào để chứng minh tính chia hết?
Phương pháp quy nạp toán học trong đó chúng ta đi từ phát biểu riêng đến phát biểu khái quát thỉnh thoảng có thể được sử dụng để chứng minh một số kết quả về tính chia hết.
Lấy ví dụ, chúng ta chứng minh rằng 32n – 2n – 1 là chia hết cho 2, với mọi giá trị nguyên dương của n.
Ta hãy kí hiệu biểu thức trên là f(n), khi đó
f(n) = 32n – 2n – 1 (1)
biến đổi n thành n + 1 ta có
f(n + 1) = 32n+2 – 2(n + 2) – 1
= 9. 32n – 2n – 3 (2)
Nhân (1) với 9, rồi lấy (2) trừ (1), ta được
f(n + 1) – 9f(n) = – 2n – 3 – 9 (–2n – 1)
= –2n – 3 + 18 n + 9
= 16n + 6
= 2 (8n + 3)
Do đó, nếu f(n) chia hết cho 2, thì f(n + 1) cũng chia hết cho 2.
Cụ thể, f(1) = 32 – 2 – 1 = 6, chia hết cho 2, nên f(2) chia hết cho 2, rồi f(3) cũng vậy, cứ thế. Như vậy, kết quả là đúng cho mọi trường hợp.
Những kết quả sau đây có thể được chứng minh tương tự:
i) 10n + 3.42+2 + 5 là chia hết cho 9
ii) 34n+2 + 52n+1 là chia hết cho 14
iii) 32n+2 – 8n – 9 là chia hết cho 64
iv) 32n+5 + 160n2 – 56n – 243 là chia hết cho 512
v) 52n+2 – 24n – 25 là chia hết cho 576.
44. Các số Pythagoras là gì?
Các số nguyên dương x, y, z được gọi là số Pythagoras nếu chúng thỏa mãn phương trình: x2 + y2 = z2.
Hai ví dụ quen thuộc của những số như thế là 3, 4, 5 và 5, 12, 13.
Ở đây ta có 32 + 42 = 52, và 52 + 122 = 132.
Các số Pythagoras luôn làm thành ba cạnh của một tam giác vuông.
Đặc điểm nổi bật nhất của tam giác vuông được cho bởi định lí Pythagoras. Định lí phát biểu rằng tổng bình phương của hai cạnh góc vuông bằng bình phương của cạnh huyền.
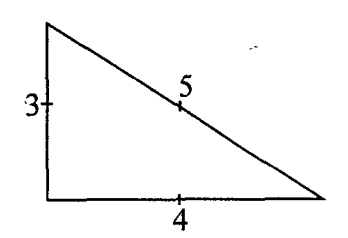
Theo định lí Pythagoras, 32 + 42 = 52.
Các số như vậy được cho bởi
x = m2 – n2
y = 2mn
z = m2 + n2
Trong đó m, n là hai số nguyên dương bất kì, và m lớn hơn n.
45. Còn tổng lũy thừa cao nhất của các số nguyên thì sao? Hay định lí cuối cùng của Fermat là gì?
Một động thái tự nhiên là tìm kiếm các số nguyên dương x, y, z thỏa mãn
x3 + y3 = z3
x4 + y4 = z4
x5 + y5 = z5, và vân vân.
Tất cả những trường hợp này được gộp chung lại như sau:
Tìm các số nguyên x, y, z sao cho xn + yn = zn ,trong đó n là một số nguyên lớn hơn 2.
Vào khoảng năm 1637, Fermat đã dành thời gian nghiên cứu bài toán này và đi tới kết luận rằng không thể tìm được những số nguyên như thế.
Kết quả này được gọi là định lí cuối cùng của Fermat.
Ông có đề cập rằng ông đã tìm ra một cách chứng minh không thể chối cãi của kết quả này, nhưng lề của quyển sách chỗ ông viết là quá hẹp để ghi nó ra. Fermat có thói quen ghi lại một số ý tưởng của ông trên lề của những quyển sách toán của ông.
46. Phép chứng minh đó có được tìm thấy lại hay không?
Một số nhà toán học trong hơn ba trăm năm qua đã cố gắng tìm lại phép chứng minh đó nhưng chẳng có ai thành công.
Định lí đã được chứng minh cho một vài giá trị của n, và người ta chưa tìm thấy ngoại lệ nào, nhưng một chứng minh tổng quát đúng cho mọi giá trị của n cho đến nay vẫn còn né tránh các nhà toán học.
47. Mỗi số nguyên dương có thể được biểu diễn theo tổng của bốn bình phương hay không?
Một tính chất thú vị đúng cho mọi số nguyên dương là mỗi số nguyên như thế có thể được biểu diễn ở dạng x2 + y2 + z2 + u2, các giá trị bằng 0 của x, y, z, u là không thể tránh khỏi.
Ví dụ,
1 = 02 + 02 + 02 + 12
2 = 02 + 02 + 12 + 12
3 = 02 + 12 + 12 + 12
4 = 12 + 12 + 12 + 12
5 = 02 + 02 + 12 + 22
6 = 02 + 12 + 12 + 22
7 = 12 + 12 + 12 + 22
Vân vân.
50 = 02 + 02 + 12 + 72
234 = 22 + 52 + 62 + 132
2011 = 132 + 162 + 192 + 352
Vân vân.
48. Các biểu diễn như trên có là duy nhất hay không?
Không. Có thể biểu diễn một con số theo kiểu như vậy bằng nhiều cách. Ví dụ
10007 = 992 + 142 + 32 + 12
= 742 + 652 + 152 + 92
= 622 + 592 + 512 + 92
49. Những kết quả như thế có tồn tại cho số mũ nguyên 3 và số mũ cao hơn hay không?
Các nghiên cứu đã được thực hiện theo chiều hướng này kể từ năm 1770 và các kết quả liên tục được cải thiện.
Những kết quả thu được cho đến nay đủ để phát biểu rằng mỗi số nguyên N đủ lớn là tổng của 9 mũ 3, 19 mũ 4, 41 mũ 5, 87 mũ 6, 193 mũ 7, 425 mũ 8, 949 mũ 9 hoặc 2113 mũ 10.
Giới hạn trên của số N chưa được xác định, nhưng nó phải là rất lớn.
50. Giả thiết Goldbach về những con số lớn là gì?
Vào năm 1742, Goldbach đã nêu giả thiết rằng mỗi con số lẻ N đủ lớn có thể được biểu diễn bằng tổng của ba số nguyên tố, tức là
Số lẻ N = p1 + p2 + p3
nhưng giả thiết thật ra được chứng minh bởi Vinogradov vào năm 1937.
Nếu chúng ta cộng thêm 3 vào hai vế của biểu thức liên hệ này, thì ta có
Số chẵn N = p1 + p2 + p3 + 3
tức là mỗi con số chẵn đủ lớn có thể được biểu diễn bằng tổng của bốn số nguyên tố.
Người ta còn biết rằng mỗi số nguyên đủ lớn là tổng của tối đa 20 số nguyên tố.
Toán học – Những điều kì thú và những mốc son lịch sử
A.L. Audichya
Trần Nghiêm dịch
Phần tiếp theo >>